In fluid mechanics, the Grashof number is a dimensionless number which approximates the ratio of the buoyancy to viscous forces acting on a fluid. It frequently arises in the study of situations involving natural convection and is analogous to the Reynolds number.
In fluid mechanics, the Rayleigh number (Ra, after Lord Rayleigh) for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free (or natural) convection. It characterises the fluid's flow regime: a value in a certain lower range denotes laminar flow; a value in a higher range, turbulent flow. Below a certain critical value, there is no fluid motion and heat transfer is by conduction rather than convection. For most engineering purposes, the Rayleigh number is large, somewhere around 106 to 108.
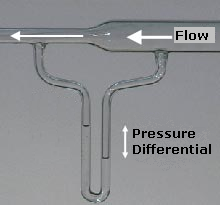
Bernoulli's principle is a key concept in fluid dynamics that relates pressure, speed and height. Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or the fluid's potential energy. The principle is named after the Swiss mathematician and physicist Daniel Bernoulli, who published it in his book Hydrodynamica in 1738. Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler in 1752 who derived Bernoulli's equation in its usual form.
In fluid dynamics, the drag equation is a formula used to calculate the force of drag experienced by an object due to movement through a fully enclosing fluid. The equation is:

In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment, such as air or water. It is used in the drag equation in which a lower drag coefficient indicates the object will have less aerodynamic or hydrodynamic drag. The drag coefficient is always associated with a particular surface area.
In fluid dynamics, the Darcy–Weisbach equation is an empirical equation that relates the head loss, or pressure loss, due to friction along a given length of pipe to the average velocity of the fluid flow for an incompressible fluid. The equation is named after Henry Darcy and Julius Weisbach. Currently, there is no formula more accurate or universally applicable than the Darcy-Weisbach supplemented by the Moody diagram or Colebrook equation.

Terminal velocity is the maximum velocity (speed) attainable by an object as it falls through a fluid. It occurs when the sum of the drag force (Fd) and the buoyancy is equal to the downward force of gravity (FG) acting on the object. Since the net force on the object is zero, the object has zero acceleration. For objects falling through regular air, the buoyant force is usually dismissed and not taken into account as its effects are negligible.
In fluid dynamics, the lift coefficient is a dimensionless quantity that relates the lift generated by a lifting body to the fluid density around the body, the fluid velocity and an associated reference area. A lifting body is a foil or a complete foil-bearing body such as a fixed-wing aircraft. CL is a function of the angle of the body to the flow, its Reynolds number and its Mach number. The section lift coefficient cl refers to the dynamic lift characteristics of a two-dimensional foil section, with the reference area replaced by the foil chord.
The Hagen number (Hg) is a dimensionless number used in forced flow calculations. It is the forced flow equivalent of the Grashof number and was named after the German hydraulic engineer G. H. L. Hagen.
There are two different Bejan numbers (Be) used in the scientific domains of thermodynamics and fluid mechanics. Bejan numbers are named after Adrian Bejan.

The Weber number (We) is a dimensionless number in fluid mechanics that is often useful in analysing fluid flows where there is an interface between two different fluids, especially for multiphase flows with strongly curved surfaces. It is named after Moritz Weber (1871–1951). It can be thought of as a measure of the relative importance of the fluid's inertia compared to its surface tension. The quantity is useful in analyzing thin film flows and the formation of droplets and bubbles.
In fluid dynamics, drag is a force acting opposite to the relative motion of any object moving with respect to a surrounding fluid. This can exist between two fluid layers or between a fluid and a solid surface.
In fluid mechanics, added mass or virtual mass is the inertia added to a system because an accelerating or decelerating body must move some volume of surrounding fluid as it moves through it. Added mass is a common issue because the object and surrounding fluid cannot occupy the same physical space simultaneously. For simplicity this can be modeled as some volume of fluid moving with the object, though in reality "all" the fluid will be accelerated, to various degrees.

The Stokes number (Stk), named after George Gabriel Stokes, is a dimensionless number characterising the behavior of particles suspended in a fluid flow. The Stokes number is defined as the ratio of the characteristic time of a particle to a characteristic time of the flow or of an obstacle, or
The Stanton number, St, is a dimensionless number that measures the ratio of heat transferred into a fluid to the thermal capacity of fluid. The Stanton number is named after Thomas Stanton (engineer) (1865–1931). It is used to characterize heat transfer in forced convection flows.
In fluid dynamics, the Morton number (Mo) is a dimensionless number used together with the Eötvös number or Bond number to characterize the shape of bubbles or drops moving in a surrounding fluid or continuous phase, c. It is named after Rose Morton, who described it with W. L. Haberman in 1953.
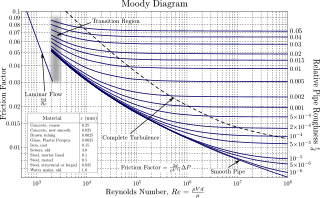
In engineering, the Moody chart or Moody diagram is a graph in non-dimensional form that relates the Darcy–Weisbach friction factor fD, Reynolds number Re, and surface roughness for fully developed flow in a circular pipe. It can be used to predict pressure drop or flow rate down such a pipe.
In a nozzle or other constriction, the discharge coefficient is the ratio of the actual discharge to the ideal discharge, i.e., the ratio of the mass flow rate at the discharge end of the nozzle to that of an ideal nozzle which expands an identical working fluid from the same initial conditions to the same exit pressures.
Blade element momentum theory is a theory that combines both blade element theory and momentum theory. It is used to calculate the local forces on a propeller or wind-turbine blade. Blade element theory is combined with momentum theory to alleviate some of the difficulties in calculating the induced velocities at the rotor.
Skin friction drag is a type of aerodynamic or hydrodynamic drag, which is resistant force exerted on an object moving in a fluid. Skin friction drag is caused by the viscosity of fluids and is developed from laminar drag to turbulent drag as a fluid moves on the surface of an object. Skin friction drag is generally expressed in terms of the Reynolds number, which is the ratio between inertial force and viscous force.












