
In fluid dynamics, gravity waves are waves generated in a fluid medium or at the interface between two media when the force of gravity or buoyancy tries to restore equilibrium. An example of such an interface is that between the atmosphere and the ocean, which gives rise to wind waves.
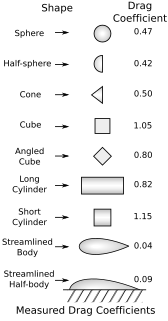
In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment, such as air or water. It is used in the drag equation in which a lower drag coefficient indicates the object will have less aerodynamic or hydrodynamic drag. The drag coefficient is always associated with a particular surface area.

The Poincaré group, named after Henri Poincaré (1906), was first defined by Hermann Minkowski (1908) as the group of Minkowski spacetime isometries. It is a ten-dimensional non-abelian Lie group, which is of importance as a model in our understanding the most basic fundamentals of physics.

In statistics, a sequence of random variables is homoscedastic if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings homoskedasticity and heteroskedasticity are also frequently used.
The lift coefficient (CL) is a dimensionless coefficient that relates the lift generated by a lifting body to the fluid density around the body, the fluid velocity and an associated reference area. A lifting body is a foil or a complete foil-bearing body such as a fixed-wing aircraft. CL is a function of the angle of the body to the flow, its Reynolds number and its Mach number. The section lift coefficient cl refers to the dynamic lift characteristics of a two-dimensional foil section, with the reference area replaced by the foil chord.
A Maxwell material is a viscoelastic material having the properties both of elasticity and viscosity. It is named for James Clerk Maxwell who proposed the model in 1867. It is also known as a Maxwell fluid.

The Rayleigh–Taylor instability, or RT instability, is an instability of an interface between two fluids of different densities which occurs when the lighter fluid is pushing the heavier fluid. Examples include the behavior of water suspended above oil in the gravity of Earth, mushroom clouds like those from volcanic eruptions and atmospheric nuclear explosions, supernova explosions in which expanding core gas is accelerated into denser shell gas, instabilities in plasma fusion reactors and inertial confinement fusion.
In fluid dynamics, drag is a force acting opposite to the relative motion of any object moving with respect to a surrounding fluid. This can exist between two fluid layers or a fluid and a solid surface. Unlike other resistive forces, such as dry friction, which are nearly independent of velocity, drag force depends on velocity.

In the theory of general relativity, linearized gravity is the application of perturbation theory to the metric tensor that describes the geometry of spacetime. As a consequence, linearized gravity is an effective method for modeling the effects of gravity when the gravitational field is weak. The usage of linearized gravity is integral to the study of gravitational waves and weak-field gravitational lensing.
In mathematical physics, the gamma matrices, , also known as the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra Cl1,3(). It is also possible to define higher-dimensional gamma matrices. When interpreted as the matrices of the action of a set of orthogonal basis vectors for contravariant vectors in Minkowski space, the column vectors on which the matrices act become a space of spinors, on which the Clifford algebra of spacetime acts. This in turn makes it possible to represent infinitesimal spatial rotations and Lorentz boosts. Spinors facilitate spacetime computations in general, and in particular are fundamental to the Dirac equation for relativistic spin-1/2 particles.
In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow, i.e. flows in which the plate is not parallel to the flow.

In relativistic physics, the electromagnetic stress–energy tensor is the contribution to the stress–energy tensor due to the electromagnetic field. The stress–energy tensor describes the flow of energy and momentum in spacetime. The electromagnetic stress–energy tensor contains the negative of the classical Maxwell stress tensor that governs the electromagnetic interactions.

The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form that is manifestly invariant under Lorentz transformations, in the formalism of special relativity using rectilinear inertial coordinate systems. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another. However, this is not as general as Maxwell's equations in curved spacetime or non-rectilinear coordinate systems.

In physics, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field in curved spacetime or where one uses an arbitrary coordinate system. These equations can be viewed as a generalization of the vacuum Maxwell's equations which are normally formulated in the local coordinates of flat spacetime. But because general relativity dictates that the presence of electromagnetic fields induce curvature in spacetime, Maxwell's equations in flat spacetime should be viewed as a convenient approximation.
The 't Hooft η symbol is a symbol which allows one to express the generators of the SU(2) Lie algebra in terms of the generators of Lorentz algebra. The symbol is a blend between the Kronecker delta and the Levi-Civita symbol. It was introduced by Gerard 't Hooft. It is used in the construction of the BPST instanton.
In statistics, Bayesian multivariate linear regression is a Bayesian approach to multivariate linear regression, i.e. linear regression where the predicted outcome is a vector of correlated random variables rather than a single scalar random variable. A more general treatment of this approach can be found in the article MMSE estimator.

The neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid. All fibers on one side of the neutral axis are in a state of tension, while those on the opposite side are in compression.
In flight dynamics, longitudinal static stability is the stability of an aircraft in the longitudinal, or pitching, plane under steady flight conditions. This characteristic is important in determining whether a human pilot will be able to control the aircraft in the pitching plane without requiring excessive attention or excessive strength.
The Clausius–Duhem inequality is a way of expressing the second law of thermodynamics that is used in continuum mechanics. This inequality is particularly useful in determining whether the constitutive relation of a material is thermodynamically allowable.
Generalized relative entropy is a measure of dissimilarity between two quantum states. It is a "one-shot" analogue of quantum relative entropy and shares many properties of the latter quantity.

























