 | This article may be too technical for most readers to understand.(November 2013) |
Dynamical heterogeneity describes the behavior of glass-forming materials when undergoing a phase transition from the liquid state to the glassy state. In dynamical heterogeneity, the dynamics of cooling to a glassy state show variation within the material.
Polymer properties include viscoelasticity and may be synthetic or natural. When a polymeric liquid is cooled below its freezing temperature without crystallizing, it becomes a supercooled liquid. When the supercooled liquid is further cooled, it becomes a glass. [1]
The temperature at which a polymer becomes a glass by fast cooling is called the glass transition temperature Tg. At this temperature, viscosity reaches up to 1013 poise depending upon cooling-rate.
It is possible for a phase transition from polymer to glassy state to take place. Polymer glass transitions have many determinants including relaxation time, viscosity and cage size. At low temperatures the dynamics become very slow (sluggish) and relaxation time increases from picoseconds to seconds, minutes, or more. At high temperatures, the correlation function has a ballistic regime for very short times (when particles do not interact) and a microscopic regime. In the microscopic regime, the correlation functions decay exponentially at high temperatures. At low temperatures the correlation functions have an intermediate regime in which particles have both slow and fast relaxations. The slow relaxation is an indication of cages in the glassy system. In glassy state density is not homogeneous i.e. particles are localized in different density distributions in space. It means that density fluctuations are present in the system. Particle dynamics become very slow because temperature is directly proportional to kinetic energy causing the particles trapped in local regions by each other. Particles are doing rattling motion inside these cages and cooperate with each other. These regions in the glassy polymer are called cages. In the intermediate regime each particle has its own and different relaxation time. [2]
The dynamics in all these cases are different, so at a small scale, there are a large number of cages in the system relative to the size of the whole system. This is known as dynamical heterogeneity in the glassy state of the system. A measurement of dynamical heterogeneity can be done by calculating correlation functions like Non-Gaussian parameter, four point correlation functions (Dynamic Susceptibility) and three time correlation functions. [3]
Melting, or fusion, is a physical process that results in the phase transition of a substance from a solid to a liquid. This occurs when the internal energy of the solid increases, typically by the application of heat or pressure, which increases the substance's temperature to the melting point. At the melting point, the ordering of ions or molecules in the solid breaks down to a less ordered state, and the solid melts to become a liquid.
Rheology is the study of the flow of matter, primarily in a fluid state but also as "soft solids" or solids under conditions in which they respond with plastic flow rather than deforming elastically in response to an applied force. Rheology is the branch of physics that deals with the deformation and flow of materials, both solids and liquids.
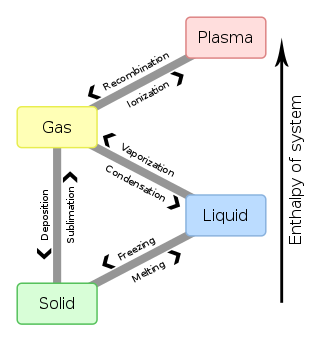
In chemistry, thermodynamics, and other related fields like physics and biology, a phase transition is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of matter: solid, liquid, and gas, and in rare cases, plasma. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point.
In physics, critical phenomena is the collective name associated with the physics of critical points. Most of them stem from the divergence of the correlation length, but also the dynamics slows down. Critical phenomena include scaling relations among different quantities, power-law divergences of some quantities described by critical exponents, universality, fractal behaviour, and ergodicity breaking. Critical phenomena take place in second order phase transitions, although not exclusively.
?
Complex fluids are mixtures that have a coexistence between two phases: solid–liquid, solid–gas (granular), liquid–gas (foams) or liquid–liquid (emulsions). They exhibit unusual mechanical responses to applied stress or strain due to the geometrical constraints that the phase coexistence imposes. The mechanical response includes transitions between solid-like and fluid-like behavior as well as fluctuations. Their mechanical properties can be attributed to characteristics such as high disorder, caging, and clustering on multiple length scales.
Polyamorphism is the ability of a substance to exist in several different amorphous modifications. It is analogous to the polymorphism of crystalline materials. Many amorphous substances can exist with different amorphous characteristics. However, polyamorphism requires two distinct amorphous states with a clear, discontinuous (first-order) phase transition between them. When such a transition occurs between two stable liquid states, a polyamorphic transition may also be referred to as a liquid–liquid phase transition.
Thermomechanical analysis (TMA) is a technique used in thermal analysis, a branch of materials science which studies the properties of materials as they change with temperature.
The time–temperature superposition principle is a concept in polymer physics and in the physics of glass-forming liquids.
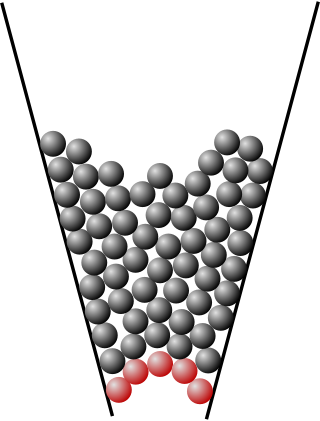
Jamming is the physical process by which the viscosity of some mesoscopic materials, such as granular materials, glasses, foams, polymers, emulsions, and other complex fluids, increases with increasing particle density. The jamming transition has been proposed as a new type of phase transition, with similarities to a glass transition but very different from the formation of crystalline solids.
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity is defined scientifically as a force multiplied by a time divided by an area. Thus its SI units are newton-seconds per square meter, or pascal-seconds.
A liquid is a nearly incompressible fluid that conforms to the shape of its container but retains a nearly constant volume independent of pressure. It is one of the four fundamental states of matter, and is the only state with a definite volume but no fixed shape.
The glass–liquid transition, or glass transition, is the gradual and reversible transition in amorphous materials from a hard and relatively brittle "glassy" state into a viscous or rubbery state as the temperature is increased. An amorphous solid that exhibits a glass transition is called a glass. The reverse transition, achieved by supercooling a viscous liquid into the glass state, is called vitrification.
Johari–Goldstein relaxation, also known as the JG β-relaxation, is a universal property of glasses and certain other disordered materials. Proposed in 1969 by Martin Goldstein, JG β-relaxation were described as a secondary relaxation mechanism required to explain the viscosity behavior of liquids approaching the glass transition in the potential energy landscape picture presented in Goldstein's seminal 1969 paper. Previous experiments on glass forming liquids showed multiple relaxation times present in liquids measured by time dependent compliance measurements. Gyan Johari and Martin Goldstein measured the dielectric loss spectrum of a set of rigid glass forming molecules to further test the hypothesis of Goldstein in 1969. The relaxation, a peak in mechanical or dielectric loss at a particular frequency, had previously been attributed to a type of molecular flexibility. The fact that such a loss peak shows up in glasses of rigid molecules lacking this flexibility demonstrated its universal character.
In condensed matter physics and physical chemistry, the terms viscous liquid, supercooled liquid, and glass forming liquid are often used interchangeably to designate liquids that are at the same time highly viscous, can be or are supercooled, and able to form a glass.
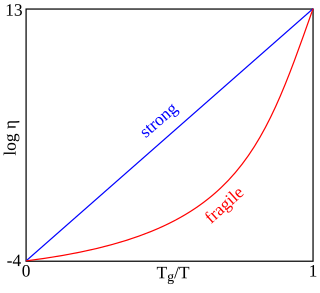
In glass sciences, fragility or "kinetic fragility" is a concept proposed by the Australian-American physical chemist C. Austen Angell. Fragility characterizes how rapidly the viscosity of a glass forming liquid approaches a very large value approximately 1012 Pa s during cooling. At this viscosity, the liquid is "frozen" into a solid and the corresponding temperature is known as the glass transition temperature Tg. Materials with a higher fragility have a more rapid increase in viscosity as approaching Tg, while those with a lower fragility have a slower increase in viscosity. Fragility is one of the most important concepts to understand viscous liquids and glasses. Fragility may be related to the presence of dynamical heterogeneity in glass forming liquids, as well as to the breakdown of the usual Stokes–Einstein relationship between viscosity and diffusion. Fragility has no direct relationship with the colloquial meaning of the word "fragility", which more closely relates to the brittleness of a material.
Sharon C. Glotzer is an American scientist and "digital alchemist", the Anthony C. Lembke Department Chair of Chemical Engineering, the John Werner Cahn Distinguished University Professor of Engineering and the Stuart W. Churchill Collegiate Professor of Chemical Engineering at the University of Michigan, where she is also professor of materials science and engineering, professor of physics, professor of macromolecular science and engineering, and professor of applied physics. She is recognized for her contributions to the fields of soft matter and computational science, most notably on problems in assembly science and engineering, nanoscience, and the glass transition, for which the elucidation of the nature of dynamical heterogeneity in glassy liquids is of particular significance. She is a member of the National Academy of Sciences, the National Academy of Engineering, and the American Academy of Arts and Sciences.
Biman Bagchi is an Indian scientist currently serving as a SERB-DST National Science Chair Professor and Honorary Professor at the Solid State and Structural Chemistry Unit of the Indian Institute of Science. He is a theoretical physical chemist and biophysicist known for his research in the area of statistical mechanics; particularly in the study of phase transition and nucleation, solvation dynamics, mode-coupling theory of electrolyte transport, dynamics of biological macromolecules, protein folding, enzyme kinetics, supercooled liquids and protein hydration layer. He is an elected fellow of the Indian National Science Academy, the Indian Academy of Sciences, The World Academy of Sciences and an International honorary member of the American Academy of Arts and Sciences. Along with several scientific articles, he has authored three books, (i) Molecular Relaxation in Liquids, (ii) Water in Biological and Chemical Processes: From Structure and Dynamics to Function, and (iii) Statistical Mechanics for Chemistry and Materials Science.
Cooperative segmental mobility is a phenomenon associated with mobility of tens to a few hundreds of repeat units of a polymer and is important in defining the transition between “glassy” and “rubbery” state of the polymer. This cooperative segmental mobility is closely related to the dynamics of the polymer near its glass transition temperature. In the glassy state, the relaxation process of a polymer chain is a cooperative phenomenon and the molecular motion depends to some degree on that of its neighbors.
Mechanics of gelation describes processes relevant to sol-gel process.
{{cite journal}}: Cite journal requires |journal= (help)