Butler-Volmer equation
An elementary charge transfer step can be described by the Butler–Volmer model proposed by John Alfred Valentine Butler and Max Volmer. The reaction rate is given by the Butler-Volmer equation: [1]
In this equation 
is the net current density, 
is the exchange current density, 
is the charge transfer coefficient, 
is the number of electrons transferred in the reaction, 
is the Faraday constant, 
is the molar gas constant, 
is the absolute temperature, 
is the electrode overpotential, 
is the thermodynamic equilibrium reduction potential and 
is the observed value of this potential.
The equation yields a negative current density for a reduction reaction (negative overpotential) and a positive current density for an oxidation reaction (positive overpotential). The sign of the current density has no physical meaning and is defined by an international convention.
In electrochemistry, the Nernst equation is a chemical thermodynamical relationship that permits the calculation of the reduction potential of a reaction from the standard electrode potential, absolute temperature, the number of electrons involved in the redox reaction, and activities of the chemical species undergoing reduction and oxidation respectively. It was named after Walther Nernst, a German physical chemist who formulated the equation.
In electrochemistry, the standard hydrogen electrode, is a redox electrode which forms the basis of the thermodynamic scale of oxidation-reduction potentials. Its absolute electrode potential is estimated to be 4.44 ± 0.02 V at 25 °C, but to form a basis for comparison with all other electrochemical reactions, hydrogen's standard electrode potential is declared to be zero volts at any temperature. Potentials of all other electrodes are compared with that of the standard hydrogen electrode at the same temperature.
In electrochemistry, cyclic voltammetry (CV) is a type of potentiodynamic measurement. In a cyclic voltammetry experiment, the working electrode potential is ramped linearly versus time. Unlike in linear sweep voltammetry, after the set potential is reached in a CV experiment, the working electrode's potential is ramped in the opposite direction to return to the initial potential. These cycles of ramps in potential may be repeated as many times as needed. The current at the working electrode is plotted versus the applied voltage to give the cyclic voltammogram trace. Cyclic voltammetry is generally used to study the electrochemical properties of an analyte in solution or of a molecule that is adsorbed onto the electrode.
The Rayleigh–Taylor instability, or RT instability, is an instability of an interface between two fluids of different densities which occurs when the lighter fluid is pushing the heavier fluid. Examples include the behavior of water suspended above oil in the gravity of Earth, mushroom clouds like those from volcanic eruptions and atmospheric nuclear explosions, supernova explosions in which expanding core gas is accelerated into denser shell gas, instabilities in plasma fusion reactors and inertial confinement fusion.
Dielectric spectroscopy measures the dielectric properties of a medium as a function of frequency. It is based on the interaction of an external field with the electric dipole moment of the sample, often expressed by permittivity.
The principle of detailed balance can be used in kinetic systems which are decomposed into elementary processes. It states that at equilibrium, each elementary process is in equilibrium with its reverse process.
Voltammetry is a category of electroanalytical methods used in analytical chemistry and various industrial processes. In voltammetry, information about an analyte is obtained by measuring the current as the potential is varied. The analytical data for a voltammetric experiment comes in the form of a voltammogram, which plots the current produced by the analyte versus the potential of the working electrode.
In electrochemistry, overpotential is the potential difference (voltage) between a half-reaction's thermodynamically determined reduction potential and the potential at which the redox event is experimentally observed. The term is directly related to a cell's voltage efficiency. In an electrolytic cell the existence of overpotential implies that the cell requires more energy than thermodynamically expected to drive a reaction. In a galvanic cell the existence of overpotential means less energy is recovered than thermodynamics predicts. In each case the extra/missing energy is lost as heat. The quantity of overpotential is specific to each cell design and varies across cells and operational conditions, even for the same reaction. Overpotential is experimentally determined by measuring the potential at which a given current density is achieved.
In relativistic physics, the electromagnetic stress–energy tensor is the contribution to the stress–energy tensor due to the electromagnetic field. The stress–energy tensor describes the flow of energy and momentum in spacetime. The electromagnetic stress–energy tensor contains the negative of the classical Maxwell stress tensor that governs the electromagnetic interactions.
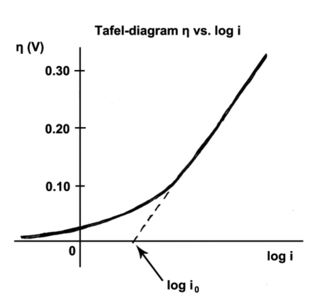
The Tafel equation is an equation in electrochemical kinetics relating the rate of an electrochemical reaction to the overpotential. The Tafel equation was first deduced experimentally and was later shown to have a theoretical justification. The equation is named after Swiss chemist Julius Tafel.
It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction.
The Stern–Volmer relationship, named after Otto Stern and Max Volmer, allows the kinetics of a photophysical intermolecular deactivation process to be explored.
In electrochemistry, the Butler–Volmer equation, also known as Erdey-Grúz–Volmer equation, is one of the most fundamental relationships in electrochemical kinetics. It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction, considering that both a cathodic and an anodic reaction occur on the same electrode:
In probability and statistics, the Gompertz distribution is a continuous probability distribution, named after Benjamin Gompertz. The Gompertz distribution is often applied to describe the distribution of adult lifespans by demographers and actuaries. Related fields of science such as biology and gerontology also considered the Gompertz distribution for the analysis of survival. More recently, computer scientists have also started to model the failure rates of computer code by the Gompertz distribution. In Marketing Science, it has been used as an individual-level simulation for customer lifetime value modeling. In network theory, particularly the Erdős–Rényi model, the walk length of a random self-avoiding walk (SAW) is distributed according to the Gompertz distribution.
In electrochemistry, exchange current density is a parameter used in the Tafel equation, Butler–Volmer equation and other electrochemical kinetics expressions. The Tafel equation describes the dependence of current for an electrolytic process to overpotential.
Charge transfer coefficient, and symmetry factor are two related parameters used in description of the kinetics of electrochemical reactions. They appear in the Butler–Volmer equation and related expressions.
Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is thermal energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.
In electrochemistry, protein film voltammetry is a technique for examining the behavior of proteins immobilized on an electrode. The technique is applicable to proteins and enzymes that engage in electron transfer reactions and it is part of the methods available to study enzyme kinetics.
The Koutecký–Levich equation models the measured electric current at an electrode from an electrochemical reaction in relation to the kinetic activity and the mass transport of reactants.
The shear viscosity of a fluid is a material property that describes the friction between internal neighboring fluid surfaces flowing with different fluid velocities. This friction is the effect of (linear) momentum exchange caused by molecules with sufficient energy to move between these fluid sheets due to fluctuations in their motion. The viscosity is not a material constant, but a material property that depends on temperature, pressure, fluid mixture composition, local velocity variations. This functional relationship is described by a mathematical viscosity model called a constitutive equation which is usually far more complex than the defining equation of shear viscosity. One such complicating feature is the relation between the viscosity model for a pure fluid and the model for a fluid mixture which is called mixing rules. When scientists and engineers use new arguments or theories to develop a new viscosity model, instead of improving the reigning model, it may lead to the first model in a new class of models. This article will display one or two representative models for different classes of viscosity models, and these classes are:
In fluid dynamics, the Sullivan vortex is an exact solution of the Navier–Stokes equations describing a two-celled vortex in an axially strained flow, that was discovered by Roger D. Sullivan in 1959. At large radial distances, the Sullivan vortex resembles a Burgers vortex, however, it exhibits a two-cell structure near the center, creating a downdraft at the axis and an updraft at a finite radial location. Specifically, in the outer cell, the fluid spirals inward and upward and in the inner cell, the fluid spirals down at the axis and spirals upwards at the boundary with the outer cell. Due to its multi-celled structure, the vortex is used to model tornadoes and large-scale complex vortex structures in turbulent flows.
