End-to-end delay

Last updated July 09, 2024

End-to-end delay or one-way delay (OWD) refers to the time taken for a packet to be transmitted across a network from source to destination. It is a common term in IP network monitoring, and differs from round-trip time (RTT) in that only path in the one direction from source to destination is measured.

Measurement

The ping utility measures the RTT, that is, the time to go and come back to a host. Half the RTT is often used as an approximation of OWD but this assumes that the forward and back paths are the same in terms of congestion, number of hops, or quality of service (QoS). This is not always a good assumption. To avoid such problems, the OWD may be measured directly.

Direct

OWDs may be measured between two points A and B of an IP network through the use of synchronized clocks; A records a timestamp on the packet and sends it to B, which notes the receiving time and calculates the OWD as their difference. The transmitted packets need to be identified at source and destination in order to avoid packet loss or packet reordering. However, this method suffers several limitations, such as requiring intensive cooperation between both parties, and the accuracy of the measured delay is subject to the synchronization precision.

The Minimum-Pairs Protocol is an example by which several cooperating entities, A, B, and C, could measure OWDs between one of them and a fourth less cooperative one (e.g., between B and X).^[1]

Estimate

Transmission between two network nodes may be asymmetric, and the forward and reverse delays are not equal. Half the RTT value is the average of the forward and reverse delays and so may be sometimes used as an approximation to the end-to-end delay. The accuracy of such an estimate depends on the nature of delay distribution in both directions. As delays in both directions become more symmetric, the accuracy increases.

The probability mass function (PMF) of absolute error, E, between the smaller of the forward and reverse OWDs and their average (i.e., RTT/2) can be expressed as a function of the network delay distribution as follows:^[1]

$\Pr(E=x)={\begin{cases}\displaystyle \sum _{i=0}^{\infty }f_{i}(a).f_{i}(b),&x=0,\\\displaystyle \sum _{i=0}^{\infty }f_{i}(a).f_{2x+i}(b)+\sum _{i=0}^{\infty }f_{i}(b).f_{2x+i}(a),&x>0,\end{cases}}$

where a and b are the forward and reverse edges, and f_y(z) is the PMF of delay of edge z (that is, f_y(z) = Pr{delay on edge z = y}).

Delay components

End-to-end delay in networks comes from several sources including transmission delay, propagation delay, processing delay and queuing delay.

Related Research Articles

Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions $y (x)$ of Bessel's differential equation $for an arbitrary complex number, which represents the order of the Bessel function. Although and produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of .$

In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable $, or just distribution function of, evaluated at, is the probability that will take a value less than or equal to .$

The natural logarithm of a number is its logarithm to the base of the mathematical constant $e$ , which is an irrational and transcendental number approximately equal to $2.718 281828459$ . The natural logarithm of $x$ is generally written as $ln x$ , $log e x$ , or sometimes, if the base $e$ is implicit, simply $log x$ . Parentheses are sometimes added for clarity, giving $ln(x)$ , $log e (x)$ , or $log(x)$ . This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.

In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events.

The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position and momentum, can be simultaneously known. In other words, the more accurately one property is measured, the less accurately the other property can be known.

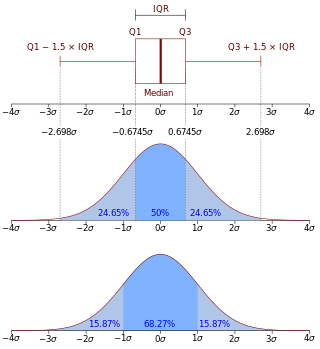
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0, the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample.

In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the distance between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate; the distance parameter could be any meaningful mono-dimensional measure of the process, such as time between production errors, or length along a roll of fabric in the weaving manufacturing process. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.

In mathematics, a power series is an infinite series of the form

In mathematics, a generating function is a representation of an infinite sequence of numbers as the coefficients of a formal power series. Unlike an ordinary series, the formal power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the "variable" remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers.

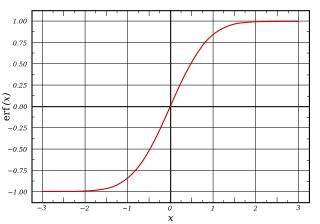
In mathematics, the error function, often denoted by $erf$ , is a function defined as:

In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be rational numbers; they may be taken in any field $K$ . In this case, one speaks of a rational function and a rational fraction over $K$ . The values of the variables may be taken in any field $L$ containing $K$ . Then the domain of the function is the set of the values of the variables for which the denominator is not zero, and the codomain is $L$ .

The Basel problem is a problem in mathematical analysis with relevance to number theory, concerning an infinite sum of inverse squares. It was first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in The Saint Petersburg Academy of Sciences. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up more than a century later by Bernhard Riemann in his seminal 1859 paper "On the Number of Primes Less Than a Given Magnitude", in which he defined his zeta function and proved its basic properties. The problem is named after Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem.

A continuous-time Markov chain (CTMC) is a continuous stochastic process in which, for each state, the process will change state according to an exponential random variable and then move to a different state as specified by the probabilities of a stochastic matrix. An equivalent formulation describes the process as changing state according to the least value of a set of exponential random variables, one for each possible state it can move to, with the parameters determined by the current state.

<span class="mw-page-title-main">Dyadic transformation</span> Doubling map on the unit interval

The dyadic transformation is the mapping

The Adomian decomposition method (ADM) is a semi-analytical method for solving ordinary and partial nonlinear differential equations. The method was developed from the 1970s to the 1990s by George Adomian, chair of the Center for Applied Mathematics at the University of Georgia. It is further extensible to stochastic systems by using the Ito integral. The aim of this method is towards a unified theory for the solution of partial differential equations (PDE); an aim which has been superseded by the more general theory of the homotopy analysis method. The crucial aspect of the method is employment of the "Adomian polynomials" which allow for solution convergence of the nonlinear portion of the equation, without simply linearizing the system. These polynomials mathematically generalize to a Maclaurin series about an arbitrary external parameter; which gives the solution method more flexibility than direct Taylor series expansion.

<span class="mw-page-title-main">Empirical distribution function</span> Distribution function associated with the empirical measure of a sample

In statistics, an empirical distribution function is the distribution function associated with the empirical measure of a sample. This cumulative distribution function is a step function that jumps up by $1/ n$ at each of the $n$ data points. Its value at any specified value of the measured variable is the fraction of observations of the measured variable that are less than or equal to the specified value.

In mathematics, the degree of a polynomial is the highest of the degrees of the polynomial's monomials with non-zero coefficients. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer. For a univariate polynomial, the degree of the polynomial is simply the highest exponent occurring in the polynomial. The term order has been used as a synonym of degree but, nowadays, may refer to several other concepts.

In probability theory and statistics, the Poisson binomial distribution is the discrete probability distribution of a sum of independent Bernoulli trials that are not necessarily identically distributed. The concept is named after Siméon Denis Poisson.

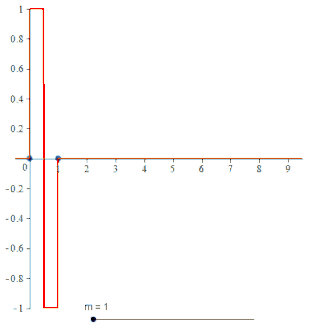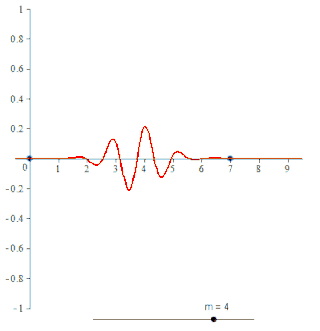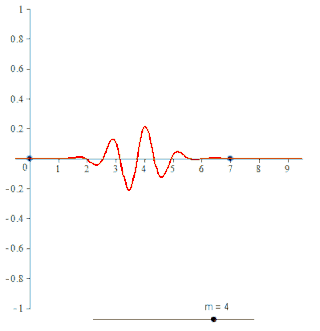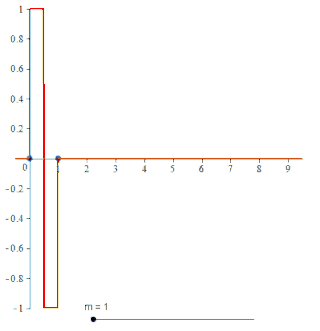
In the mathematical theory of wavelets, a spline wavelet is a wavelet constructed using a spline function. There are different types of spline wavelets. The interpolatory spline wavelets introduced by C.K. Chui and J.Z. Wang are based on a certain spline interpolation formula. Though these wavelets are orthogonal, they do not have compact supports. There is a certain class of wavelets, unique in some sense, constructed using B-splines and having compact supports. Even though these wavelets are not orthogonal they have some special properties that have made them quite popular. The terminology spline wavelet is sometimes used to refer to the wavelets in this class of spline wavelets. These special wavelets are also called B-spline wavelets and cardinal B-spline wavelets. The Battle-Lemarie wavelets are also wavelets constructed using spline functions.

The minimum-pairs is an active measurement protocol to estimate in real-time the smaller of the forward and reverse one-way network delays (OWDs). It is designed to work in hostile environments, where a set of three network nodes can estimate an upper-bound OWD between themselves and a fourth untrusted node. All four nodes must cooperate, though honest cooperation from the fourth node is not required. The objective is to conduct such estimates without involving the untrusted nodes in clock synchronization, and in a manner more accurate than simply half the round-trip time (RTT). The MP protocol can be used in delay-sensitive applications or for secure Internet geolocation.

References

1 2 Abdou, AbdelRahman; Matrawy, Ashraf; van Oorschot, Paul (May 2015). "Accurate One-Way Delay Estimation with Reduced Client-Trustworthiness". IEEE Communications Letters. 19 (5): 735–738. CiteSeerX 10.1.1.696.7425 . doi:10.1109/LCOMM.2015.2411591. S2CID 17100293.

External links

Sample delay calculations

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Abdou-1] 1 2 Abdou, AbdelRahman; Matrawy, Ashraf; van Oorschot, Paul (May 2015). "Accurate One-Way Delay Estimation with Reduced Client-Trustworthiness". IEEE Communications Letters. 19 (5): 735–738. CiteSeerX 10.1.1.696.7425 . doi:10.1109/LCOMM.2015.2411591. S2CID 17100293.

[1]