
In physics, theBardeen–Cooper–Schrieffer (BCS) theory is the first microscopic theory of superconductivity since Heike Kamerlingh Onnes's 1911 discovery. The theory describes superconductivity as a microscopic effect caused by a condensation of Cooper pairs. The theory is also used in nuclear physics to describe the pairing interaction between nucleons in an atomic nucleus.
Unconventional superconductors are materials that display superconductivity which does not conform to conventional BCS theory or its extensions.

High-temperature superconductors are defined as materials with critical temperature above 77 K, the boiling point of liquid nitrogen. They are only "high-temperature" relative to previously known superconductors, which function at even colder temperatures, close to absolute zero. The "high temperatures" are still far below ambient, and therefore require cooling. The first break through of high-temperature superconductor was discovered in 1986 by IBM researchers Georg Bednorz and K. Alex Müller. Although the critical temperature is around 35.1 K, this new type of superconductor was readily modified by Ching-Wu Chu to make the first high-temperature superconductor with critical temperature 93 K. Bednorz and Müller were awarded the Nobel Prize in Physics in 1987 "for their important break-through in the discovery of superconductivity in ceramic materials". Most high-Tc materials are type-II superconductors.

Fermi liquid theory is a theoretical model of interacting fermions that describes the normal state of most metals at sufficiently low temperatures. The interactions among the particles of the many-body system do not need to be small. The phenomenological theory of Fermi liquids was introduced by the Soviet physicist Lev Davidovich Landau in 1956, and later developed by Alexei Abrikosov and Isaak Khalatnikov using diagrammatic perturbation theory. The theory explains why some of the properties of an interacting fermion system are very similar to those of the ideal Fermi gas, and why other properties differ.
In physics, screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases, electrolytes, and charge carriers in electronic conductors . In a fluid, with a given permittivity ε, composed of electrically charged constituent particles, each pair of particles interact through the Coulomb force as
In condensed matter physics, a Cooper pair or BCS pair is a pair of electrons bound together at low temperatures in a certain manner first described in 1956 by American physicist Leon Cooper.
In condensed matter physics, the Fermi surface is the surface in reciprocal space which separates occupied from unoccupied electron states at zero temperature. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline lattice and from the occupation of electronic energy bands. The existence of a Fermi surface is a direct consequence of the Pauli exclusion principle, which allows a maximum of one electron per quantum state. The study of the Fermi surfaces of materials is called fermiology.
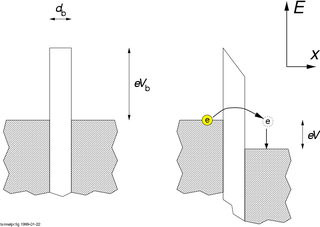
In mesoscopic physics, a Coulomb blockade (CB), named after Charles-Augustin de Coulomb's electrical force, is the decrease in electrical conductance at small bias voltages of a small electronic device comprising at least one low-capacitance tunnel junction. Because of the CB, the conductance of a device may not be constant at low bias voltages, but disappear for biases under a certain threshold, i.e. no current flows.

Spin-density wave (SDW) and charge-density wave (CDW) are names for two similar low-energy ordered states of solids. Both these states occur at low temperature in anisotropic, low-dimensional materials or in metals that have high densities of states at the Fermi level . Other low-temperature ground states that occur in such materials are superconductivity, ferromagnetism and antiferromagnetism. The transition to the ordered states is driven by the condensation energy which is approximately where is the magnitude of the energy gap opened by the transition.

In condensed matter physics, a pseudogap describes a state where the Fermi surface of a material possesses a partial energy gap, for example, a band structure state where the Fermi surface is gapped only at certain points.
In superconductivity, the superconducting coherence length, usually denoted as , is the characteristic exponent of the variations of the density of superconducting component.
The superconductor–insulator transition is an example of a quantum phase transition, whereupon tuning some parameter in the Hamiltonian, a dramatic change in the behavior of the electrons occurs. The nature of how this transition occurs is disputed, and many studies seek to understand how the order parameter, , changes. Here is the amplitude of the order parameter, and is the phase. Most theories involve either the destruction of the amplitude of the order parameter - by a reduction in the density of states at the Fermi surface, or by destruction of the phase coherence; which results from the proliferation of vortices.
A charge density wave (CDW) is an ordered quantum fluid of electrons in a linear chain compound or layered crystal. The electrons within a CDW form a standing wave pattern and sometimes collectively carry an electric current. The electrons in such a CDW, like those in a superconductor, can flow through a linear chain compound en masse, in a highly correlated fashion. Unlike a superconductor, however, the electric CDW current often flows in a jerky fashion, much like water dripping from a faucet due to its electrostatic properties. In a CDW, the combined effects of pinning and electrostatic interactions likely play critical roles in the CDW current's jerky behavior, as discussed in sections 4 & 5 below.
In solid-state physics, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons in unfilled electron bands. Electrons are one type of fermion, and when they are found in such materials, they are sometimes referred to as heavy electrons. Heavy fermion materials have a low-temperature specific heat whose linear term is up to 1000 times larger than the value expected from the free electron model. The properties of the heavy fermion compounds often derive from the partly filled f-orbitals of rare-earth or actinide ions, which behave like localized magnetic moments. The name "heavy fermion" comes from the fact that the fermion behaves as if it has an effective mass greater than its rest mass. In the case of electrons, below a characteristic temperature (typically 10 K), the conduction electrons in these metallic compounds behave as if they had an effective mass up to 1000 times the free particle mass. This large effective mass is also reflected in a large contribution to the resistivity from electron-electron scattering via the Kadowaki–Woods ratio. Heavy fermion behavior has been found in a broad variety of states including metallic, superconducting, insulating and magnetic states. Characteristic examples are CeCu6, CeAl3, CeCu2Si2, YbAl3, UBe13 and UPt3.
Cuprate superconductors are a family of high-temperature superconducting materials made of layers of copper oxides (CuO2) alternating with layers of other metal oxides, which act as charge reservoirs. At ambient pressure, cuprate superconductors are the highest temperature superconductors known. However, the mechanism by which superconductivity occurs is still not understood.
First introduced by M. Pollak, the Coulomb gap is a soft gap in the single-particle density of states (DOS) of a system of interacting localized electrons. Due to the long-range Coulomb interactions, the single-particle DOS vanishes at the chemical potential, at low enough temperatures, such that thermal excitations do not wash out the gap.
A Peierls transition or Peierls distortion is a distortion of the periodic lattice of a one-dimensional crystal. Atomic positions oscillate, so that the perfect order of the 1-D crystal is broken.
The Mattis–Bardeen theory is a theory that describes the electrodynamic properties of superconductivity. It is commonly applied in the research field of optical spectroscopy on superconductors.
In solid state physics the electronic specific heat, sometimes called the electron heat capacity, is the specific heat of an electron gas. Heat is transported by phonons and by free electrons in solids. For pure metals, however, the electronic contributions dominate in the thermal conductivity. In impure metals, the electron mean free path is reduced by collisions with impurities, and the phonon contribution may be comparable with the electronic contribution.
Kohn–Luttinger superconductivity is a theoretical mechanism for unconventional superconductivity proposed by Walter Kohn and Joaquin Mazdak Luttinger based on Friedel oscillations. In contrast to BCS theory, in which Cooper pairs are formed due to electron–phonon interaction, Kohn–Luttinger mechanism is based on fact that screened Coulomb interaction oscillates as and can create Cooper instability for non-zero angular momentum .









