
In quantum mechanics, the Pauli exclusion principle states that two or more identical particles with half-integer spins cannot simultaneously occupy the same quantum state within a system that obeys the laws of quantum mechanics. This principle was formulated by Austrian physicist Wolfgang Pauli in 1925 for electrons, and later extended to all fermions with his spin–statistics theorem of 1940.
The quantum Hall effect is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance Rxy exhibits steps that take on the quantized values
Degenerate matter occurs when the Pauli exclusion principle significantly alters a state of matter at low temperature. The term is used in astrophysics to refer to dense stellar objects such as white dwarfs and neutron stars, where thermal pressure alone is not enough to prevent gravitational collapse. The term also applies to metals in the Fermi gas approximation.

The Fermi level of a solid-state body is the thermodynamic work required to add one electron to the body. It is a thermodynamic quantity usually denoted by μ or EF for brevity. The Fermi level does not include the work required to remove the electron from wherever it came from. A precise understanding of the Fermi level—how it relates to electronic band structure in determining electronic properties; how it relates to the voltage and flow of charge in an electronic circuit—is essential to an understanding of solid-state physics.
In solid state physics, a particle's effective mass is the mass that it seems to have when responding to forces, or the mass that it seems to have when interacting with other identical particles in a thermal distribution. One of the results from the band theory of solids is that the movement of particles in a periodic potential, over long distances larger than the lattice spacing, can be very different from their motion in a vacuum. The effective mass is a quantity that is used to simplify band structures by modeling the behavior of a free particle with that mass. For some purposes and some materials, the effective mass can be considered to be a simple constant of a material. In general, however, the value of effective mass depends on the purpose for which it is used, and can vary depending on a number of factors.

Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926. Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics.

A Fermi gas is an idealized model, an ensemble of many non-interacting fermions. Fermions are particles that obey Fermi–Dirac statistics, like electrons, protons, and neutrons, and, in general, particles with half-integer spin. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density, temperature, and the set of available energy states. The model is named after the Italian physicist Enrico Fermi.

Fermi liquid theory is a theoretical model of interacting fermions that describes the normal state of the conduction electrons in most metals at sufficiently low temperatures. The theory describes the behavior of many-body systems of particles in which the interactions between particles may be strong. The phenomenological theory of Fermi liquids was introduced by the Soviet physicist Lev Davidovich Landau in 1956, and later developed by Alexei Abrikosov and Isaak Khalatnikov using diagrammatic perturbation theory. The theory explains why some of the properties of an interacting fermion system are very similar to those of the ideal Fermi gas, and why other properties differ.
In physics, screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases, electrolytes, and charge carriers in electronic conductors . In a fluid, with a given permittivity ε, composed of electrically charged constituent particles, each pair of particles interact through the Coulomb force as where the vector r is the relative position between the charges. This interaction complicates the theoretical treatment of the fluid. For example, a naive quantum mechanical calculation of the ground-state energy density yields infinity, which is unreasonable. The difficulty lies in the fact that even though the Coulomb force diminishes with distance as 1/r2, the average number of particles at each distance r is proportional to r2, assuming the fluid is fairly isotropic. As a result, a charge fluctuation at any one point has non-negligible effects at large distances.
In astrophysics and condensed matter physics, electron degeneracy pressure is a quantum mechanical effect critical to understanding the stability of white dwarf stars and metal solids. It is a manifestation of the more general phenomenon of quantum degeneracy pressure.

In condensed matter physics, the density of states (DOS) of a system describes the number of allowed modes or states per unit energy range. The density of states is defined as , where is the number of states in the system of volume whose energies lie in the range from to . It is mathematically represented as a distribution by a probability density function, and it is generally an average over the space and time domains of the various states occupied by the system. The density of states is directly related to the dispersion relations of the properties of the system. High DOS at a specific energy level means that many states are available for occupation.

A Luttinger liquid, or Tomonaga–Luttinger liquid, is a theoretical model describing interacting electrons in a one-dimensional conductor. Such a model is necessary as the commonly used Fermi liquid model breaks down for one dimension.
In condensed matter physics, the Fermi surface is the surface in reciprocal space which separates occupied from unoccupied electron states at zero temperature. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline lattice and from the occupation of electronic energy bands. The existence of a Fermi surface is a direct consequence of the Pauli exclusion principle, which allows a maximum of one electron per quantum state. The study of the Fermi surfaces of materials is called fermiology.
In solid-state physics, the free electron model is a quantum mechanical model for the behaviour of charge carriers in a metallic solid. It was developed in 1927, principally by Arnold Sommerfeld, who combined the classical Drude model with quantum mechanical Fermi–Dirac statistics and hence it is also known as the Drude–Sommerfeld model.

An ideal Bose gas is a quantum-mechanical phase of matter, analogous to a classical ideal gas. It is composed of bosons, which have an integer value of spin and abide by Bose–Einstein statistics. The statistical mechanics of bosons were developed by Satyendra Nath Bose for a photon gas and extended to massive particles by Albert Einstein, who realized that an ideal gas of bosons would form a condensate at a low enough temperature, unlike a classical ideal gas. This condensate is known as a Bose–Einstein condensate.

Angle-resolved photoemission spectroscopy (ARPES) is an experimental technique used in condensed matter physics to probe the allowed energies and momenta of the electrons in a material, usually a crystalline solid. It is based on the photoelectric effect, in which an incoming photon of sufficient energy ejects an electron from the surface of a material. By directly measuring the kinetic energy and emission angle distributions of the emitted photoelectrons, the technique can map the electronic band structure and Fermi surfaces. ARPES is best suited for the study of one- or two-dimensional materials. It has been used by physicists to investigate high-temperature superconductors, graphene, topological materials, quantum well states, and materials exhibiting charge density waves.
In materials science, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons in unfilled electron bands. Electrons are one type of fermion, and when they are found in such materials, they are sometimes referred to as heavy electrons. Heavy fermion materials have a low-temperature specific heat whose linear term is up to 1000 times larger than the value expected from the free electron model. The properties of the heavy fermion compounds often derive from the partly filled f-orbitals of rare-earth or actinide ions, which behave like localized magnetic moments.
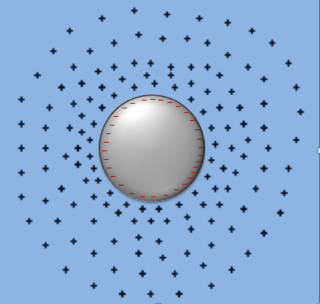
Friedel oscillations, named after French physicist Jacques Friedel, arise from localized perturbations in a metallic or semiconductor system caused by a defect in the Fermi gas or Fermi liquid. Friedel oscillations are a quantum mechanical analog to electric charge screening of charged species in a pool of ions. Whereas electrical charge screening utilizes a point entity treatment to describe the make-up of the ion pool, Friedel oscillations describing fermions in a Fermi fluid or Fermi gas require a quasi-particle or a scattering treatment. Such oscillations depict a characteristic exponential decay in the fermionic density near the perturbation followed by an ongoing sinusoidal decay resembling sinc function. In 2020, magnetic Friedel oscillations were observed on a metal surface.
Thomas–Fermi screening is a theoretical approach to calculate the effects of electric field screening by electrons in a solid. It is a special case of the more general Lindhard theory; in particular, Thomas–Fermi screening is the limit of the Lindhard formula when the wavevector is much smaller than the Fermi wavevector, i.e. the long-distance limit. It is named after Llewellyn Thomas and Enrico Fermi.
The term Dirac matter refers to a class of condensed matter systems which can be effectively described by the Dirac equation. Even though the Dirac equation itself was formulated for fermions, the quasi-particles present within Dirac matter can be of any statistics. As a consequence, Dirac matter can be distinguished in fermionic, bosonic or anyonic Dirac matter. Prominent examples of Dirac matter are graphene and other Dirac semimetals, topological insulators, Weyl semimetals, various high-temperature superconductors with -wave pairing and liquid helium-3. The effective theory of such systems is classified by a specific choice of the Dirac mass, the Dirac velocity, the gamma matrices and the space-time curvature. The universal treatment of the class of Dirac matter in terms of an effective theory leads to a common features with respect to the density of states, the heat capacity and impurity scattering.
















