In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x: where k is a positive constant.
In signal processing, group delay and phase delay are functions that describe in different ways the delay times experienced by a signal’s various sinuoidal frequency components as they pass through a linear time-invariant (LTI) system.

Pink noise, 1⁄f noise, fractional noise or fractal noise is a signal or process with a frequency spectrum such that the power spectral density is inversely proportional to the frequency of the signal. In pink noise, each octave interval carries an equal amount of noise energy.

Soil erosion is the denudation or wearing away of the upper layer of soil. It is a form of soil degradation. This natural process is caused by the dynamic activity of erosive agents, that is, water, ice (glaciers), snow, air (wind), plants, and animals. In accordance with these agents, erosion is sometimes divided into water erosion, glacial erosion, snow erosion, wind (aeolian) erosion, zoogenic erosion and anthropogenic erosion such as tillage erosion. Soil erosion may be a slow process that continues relatively unnoticed, or it may occur at an alarming rate causing a serious loss of topsoil. The loss of soil from farmland may be reflected in reduced crop production potential, lower surface water quality and damaged drainage networks. Soil erosion could also cause sinkholes.

Sediment is a solid material that is transported to a new location where it is deposited. It occurs naturally and, through the processes of weathering and erosion, is broken down and subsequently transported by the action of wind, water, or ice or by the force of gravity acting on the particles. For example, sand and silt can be carried in suspension in river water and on reaching the sea bed deposited by sedimentation; if buried, they may eventually become sandstone and siltstone through lithification.

The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials. Basically, Ohm's law was well established and stated that the current J and voltage V driving the current are related to the resistance R of the material. The inverse of the resistance is known as the conductance. When we consider a metal of unit length and unit cross sectional area, the conductance is known as the conductivity, which is the inverse of resistivity. The Drude model attempts to explain the resistivity of a conductor in terms of the scattering of electrons by the relatively immobile ions in the metal that act like obstructions to the flow of electrons.

In mathematics, a Dirac comb is a periodic function with the formula :=\sum _{k=-\infty }^{\infty }\delta (t-kT)} for some given period . Here t is a real variable and the sum extends over all integers k. The Dirac delta function and the Dirac comb are tempered distributions. The graph of the function resembles a comb, hence its name and the use of the comb-like Cyrillic letter sha (Ш) to denote the function.
The Havriliak–Negami relaxation is an empirical modification of the Debye relaxation model in electromagnetism. Unlike the Debye model, the Havriliak–Negami relaxation accounts for the asymmetry and broadness of the dielectric dispersion curve. The model was first used to describe the dielectric relaxation of some polymers, by adding two exponential parameters to the Debye equation:
In physics, Larmor precession is the precession of the magnetic moment of an object about an external magnetic field. The phenomenon is conceptually similar to the precession of a tilted classical gyroscope in an external torque-exerting gravitational field. Objects with a magnetic moment also have angular momentum and effective internal electric current proportional to their angular momentum; these include electrons, protons, other fermions, many atomic and nuclear systems, as well as classical macroscopic systems. The external magnetic field exerts a torque on the magnetic moment,

In ultrafast optics, spectral phase interferometry for direct electric-field reconstruction (SPIDER) is an ultrashort pulse measurement technique originally developed by Chris Iaconis and Ian Walmsley.
The Mason–Weaver equation describes the sedimentation and diffusion of solutes under a uniform force, usually a gravitational field. Assuming that the gravitational field is aligned in the z direction, the Mason–Weaver equation may be written
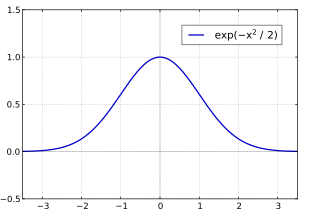
The Gabor transform, named after Dennis Gabor, is a special case of the short-time Fourier transform. It is used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time. The function to be transformed is first multiplied by a Gaussian function, which can be regarded as a window function, and the resulting function is then transformed with a Fourier transform to derive the time-frequency analysis. The window function means that the signal near the time being analyzed will have higher weight. The Gabor transform of a signal x(t) is defined by this formula:
In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators.

Sediment transport is the movement of solid particles (sediment), typically due to a combination of gravity acting on the sediment, and the movement of the fluid in which the sediment is entrained. Sediment transport occurs in natural systems where the particles are clastic rocks, mud, or clay; the fluid is air, water, or ice; and the force of gravity acts to move the particles along the sloping surface on which they are resting. Sediment transport due to fluid motion occurs in rivers, oceans, lakes, seas, and other bodies of water due to currents and tides. Transport is also caused by glaciers as they flow, and on terrestrial surfaces under the influence of wind. Sediment transport due only to gravity can occur on sloping surfaces in general, including hillslopes, scarps, cliffs, and the continental shelf—continental slope boundary.
Resonance fluorescence is the process in which a two-level atom system interacts with the quantum electromagnetic field if the field is driven at a frequency near to the natural frequency of the atom.

Stream power, originally derived by R. A. Bagnold in the 1960s, is the amount of energy the water in a river or stream is exerting on the sides and bottom of the river. Stream power is the result of multiplying the density of the water, the acceleration of the water due to gravity, the volume of water flowing through the river, and the slope of that water. There are many forms of the stream power formula with varying utilities, such as comparing rivers of various widths or quantifying the energy required to move sediment of a certain size. Stream power is closely related to other criteria such as stream competency and shear stress. Stream power is a valuable measurement for hydrologists and geomorphologists tackling sediment transport issues as well as for civil engineers, who use it in the planning and construction of roads, bridges, dams, and culverts.
Phonons can scatter through several mechanisms as they travel through the material. These scattering mechanisms are: Umklapp phonon-phonon scattering, phonon-impurity scattering, phonon-electron scattering, and phonon-boundary scattering. Each scattering mechanism can be characterised by a relaxation rate 1/ which is the inverse of the corresponding relaxation time.
Belt friction is a term describing the friction forces between a belt and a surface, such as a belt wrapped around a bollard. When a force applies a tension to one end of a belt or rope wrapped around a curved surface, the frictional force between the two surfaces increases with the amount of wrap about the curved surface, and only part of that force is transmitted to the other end of the belt or rope. Belt friction can be modeled by the Belt friction equation.

In hydrology stream competency, also known as stream competence, is a measure of the maximum size of particles a stream can transport. The particles are made up of grain sizes ranging from large to small and include boulders, rocks, pebbles, sand, silt, and clay. These particles make up the bed load of the stream. Stream competence was originally simplified by the “sixth-power-law,” which states the mass of a particle that can be moved is proportional to the velocity of the river raised to the sixth power. This refers to the stream bed velocity which is difficult to measure or estimate due to the many factors that cause slight variances in stream velocities.
The jet erosion test (JET), or jet index test, is a method used in geotechnical engineering to quantify the resistance of a soil to erosion. The test can be applied in-situ after preparing a field site, or it can be applied in a laboratory on either an intact or a remolded soil sample. A quantitative measure of erodibility allows for the prediction of erosion, assisting with the design of structures such as vegetated channels, road embankments, dams, levees, and spillways.



















