Esscher transform

Last updated March 30, 2019

In actuarial science, the Esscher transform( Gerber & Shiu 1994 ) is a transform that takes a probability density f(x) and transforms it to a new probability density f(x; h) with a parameter h. It was introduced by F. Esscher in 1932 ( Esscher 1932 ).

Actuarial science is the discipline that applies mathematical and statistical methods to assess risk in insurance, finance and other industries and professions. Actuaries are professionals trained in this discipline. In many countries, actuaries must demonstrate their competence by passing a series of rigorous professional examinations.

In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would equal that sample. In other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0, the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would equal one sample compared to the other sample.

Definition

Let f(x) be a probability density. Its Esscher transform is defined as

f(x;h)={\frac {e^{hx}f(x)}{\int _{-\infty }^{\infty }e^{hx}f(x)dx}}.\,

More generally, if μ is a probability measure, the Esscher transform of μ is a new probability measure E_h(μ) which has density

Probability measure Measure of total value one, generalizing probability distributions

In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity. The difference between a probability measure and the more general notion of measure is that a probability measure must assign value 1 to the entire probability space.

{\frac {e^{hx}}{\int _{-\infty }^{\infty }e^{hx}d\mu (x)}}

with respect to μ.

Basic properties

Combination

The Esscher transform of an Esscher transform is again an Esscher transform: E_h_₁ E_h_₂ = E_h_₁ + h₂.

Inverse

The inverse of the Esscher transform is the Esscher transform with negative parameter: E⁻¹
_h = E_−h

Mean move

The effect of the Esscher transform on the normal distribution is moving the mean:

E_{h}({\mathcal {N}}(\mu ,\,\sigma ^{2}))={\mathcal {N}}(\mu +h\sigma ^{2},\,\sigma ^{2}).\,

Examples

Distribution	Esscher transform
Bernoulli Bernoulli(p)	$\,{\frac {e^{hk}p^{k}(1-p)^{n-k}}{1-p+pe^{h}}}$
Binomial B(n, p)	$\,{\frac {{n \choose k}e^{hk}p^{k}(1-p)^{n-k}}{(1-p+pe^{h})^{n}}}$
Normal N(μ, σ²)	$\,{\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu -\sigma ^{2}h)^{2}}{2\sigma ^{2}}}}$
Poisson Pois(λ)	$\,{\frac {e^{hk-\lambda e^{h}}\lambda ^{k}}{k!}}$

Related Research Articles

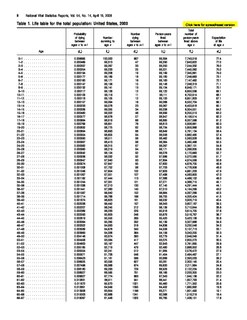
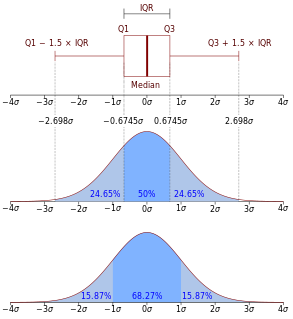
In probability theory, the normaldistribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. A random variable with a Gaussian distribution is said to be normally distributed and is called a normal deviate.

In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value.

The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto, is a power-law probability distribution that is used in description of social, scientific, geophysical, actuarial, and many other types of observable phenomena. Originally applied to describing the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population, the Pareto distribution has colloquially become known and referred to as the Pareto principle, or "80-20 rule", and is sometimes called the "Matthew principle". This rule states that, for example, 80% of the wealth of a society is held by 20% of its population. However, one should not conflate the Pareto distribution for the Pareto Principle as the former only produces this result for a particular power value, $(α = log 4 5 \approx 1.16). While is variable, empirical observation has found the 80-20 distribution to fit a wide range of cases, including natural phenomena and human activities.$

In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of $L p$ spaces.

In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the form:

In probability theory and statistics, the Rayleigh distribution is a continuous probability distribution for nonnegative-valued random variables. It is essentially a chi distribution with two degrees of freedom.

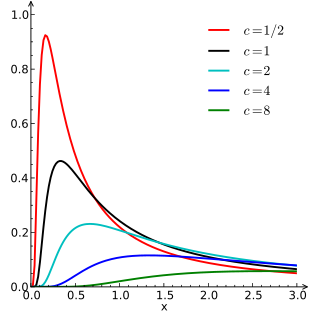
In probability theory and statistics, the Lévy distribution, named after Paul Lévy, is a continuous probability distribution for a non-negative random variable. In spectroscopy, this distribution, with frequency as the dependent variable, is known as a van der Waals profile. It is a special case of the inverse-gamma distribution. It is a stable distribution.

The scaled inverse chi-squared distribution is the distribution for x = 1/s², where s² is a sample mean of the squares of ν independent normal random variables that have mean 0 and inverse variance 1/σ² = τ². The distribution is therefore parametrised by the two quantities ν and τ², referred to as the number of chi-squared degrees of freedom and the scaling parameter, respectively.

In Bayesian probability, the Jeffreys prior, named after Sir Harold Jeffreys, is a non-informative (objective) prior distribution for a parameter space; it is proportional to the square root of the determinant of the Fisher information matrix:

In probability theory, calculation of the sum of normally distributed random variables is an instance of the arithmetic of random variables, which can be quite complex based on the probability distributions of the random variables involved and their relationships.

Differential entropy is a concept in information theory that began as an attempt by Shannon to extend the idea of (Shannon) entropy, a measure of average surprisal of a random variable, to continuous probability distributions. Unfortunately, Shannon did not derive this formula, and rather just assumed it was the correct continuous analogue of discrete entropy, but it is not. The actual continuous version of discrete entropy is the limiting density of discrete points (LDDP). Differential entropy is commonly encountered in the literature, but it is a limiting case of the LDDP, and one that loses its fundamental association with discrete entropy.

A probabilistic metric space is a generalization of metric spaces where the distance has no longer values in non-negative real numbers, but in distribution functions.

In probability and statistics, the truncated normal distribution is the probability distribution derived from that of a normally distributed random variable by bounding the random variable from either below or above. The truncated normal distribution has wide applications in statistics and econometrics. For example, it is used to model the probabilities of the binary outcomes in the probit model and to model censored data in the Tobit model.

In probability and statistics, the class of exponential dispersion models (EDM) is a set of probability distributions that represents a generalisation of the natural exponential family. Exponential dispersion models play an important role in statistical theory, in particular in generalized linear models because they have a special structure which enables deductions to be made about appropriate statistical inference.

In probability theory, the Mills ratio of a continuous random variable $is the function$

In probability theory and statistics, the normal-exponential-gamma distribution is a three-parameter family of continuous probability distributions. It has a location parameter $, scale parameter and a shape parameter .$

A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product

In probability theory, a logit-normal distribution is a probability distribution of a random variable whose logit has a normal distribution. If Y is a random variable with a normal distribution, and P is the standard logistic function, then X = P(Y) has a logit-normal distribution; likewise, if X is logit-normally distributed, then Y = logit(X)= log is normally distributed. It is also known as the logistic normal distribution, which often refers to a multinomial logit version (e.g.).

In probability theory, the rectified Gaussian distribution is a modification of the Gaussian distribution when its negative elements are reset to 0. It is essentially a mixture of a discrete distribution and a continuous distribution as a result of censoring.

References

Gerber, Hans U.; Shiu, Elias S. W. (1994). "Option Pricing by Esscher Transforms" (PDF). Transactions of the Society of Actuaries. 46: 99–191.

Esscher, F. (1932). "On the Probability Function in the Collective Theory of Risk". Skandinavisk Aktuarietidskrift. 15 (3): 175–195. doi:10.1080/03461238.1932.10405883.

In computing, a Digital Object Identifier or DOI is a persistent identifier or handle used to uniquely identify objects, standardized by the International Organization for Standardization (ISO). An implementation of the Handle System, DOIs are in wide use mainly to identify academic, professional, and government information, such as journal articles, research reports and data sets, and official publications though they also have been used to identify other types of information resources, such as commercial videos.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.