
In statistics, cluster sampling is a sampling plan used when mutually homogeneous yet internally heterogeneous groupings are evident in a statistical population. It is often used in marketing research.
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule, the quantity of interest and its result are distinguished. For example, the sample mean is a commonly used estimator of the population mean.
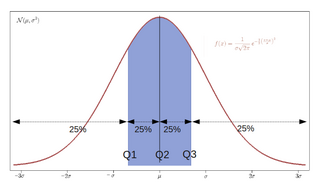
In statistics and probability, quantiles are cut points dividing the range of a probability distribution into continuous intervals with equal probabilities, or dividing the observations in a sample in the same way. There is one fewer quantile than the number of groups created. Common quantiles have special names, such as quartiles, deciles, and percentiles. The groups created are termed halves, thirds, quarters, etc., though sometimes the terms for the quantile are used for the groups created, rather than for the cut points.

In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its mean. A low standard deviation indicates that the values tend to be close to the mean of the set, while a high standard deviation indicates that the values are spread out over a wider range. The standard deviation is commonly used in the determination of what constitutes an outlier and what does not. Standard deviation may be abbreviated SD or std dev, and is most commonly represented in mathematical texts and equations by the lowercase Greek letter σ (sigma), for the population standard deviation, or the Latin letter s, for the sample standard deviation.
In statistics, point estimation involves the use of sample data to calculate a single value which is to serve as a "best guess" or "best estimate" of an unknown population parameter. More formally, it is the application of a point estimator to the data to obtain a point estimate.
Statistical bias, in the mathematical field of statistics, is a systematic tendency in which the methods used to gather data and generate statistics present an inaccurate, skewed or biased depiction of reality. Statistical bias exists in numerous stages of the data collection and analysis process, including: the source of the data, the methods used to collect the data, the estimator chosen, and the methods used to analyze the data. Data analysts can take various measures at each stage of the process to reduce the impact of statistical bias in their work. Understanding the source of statistical bias can help to assess whether the observed results are close to actuality. Issues of statistical bias has been argued to be closely linked to issues of statistical validity.
A Fermi problem, also known as an order-of-magnitude problem, is an estimation problem in physics or engineering education, designed to teach dimensional analysis or approximation of extreme scientific calculations. Fermi problems are usually back-of-the-envelope calculations. Fermi problems typically involve making justified guesses about quantities and their variance or lower and upper bounds. In some cases, order-of-magnitude estimates can also be derived using dimensional analysis. A Fermi estimate is an estimate of an extreme scientific calculation.

The standard error (SE) of a statistic is the standard deviation of its sampling distribution or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean (SEM). The standard error is a key ingredient in producing confidence intervals.
Estimation theory is a branch of statistics that deals with estimating the values of parameters based on measured empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the measured data. An estimator attempts to approximate the unknown parameters using the measurements. In estimation theory, two approaches are generally considered:
Sample size determination or estimation is the act of choosing the number of observations or replicates to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample. In practice, the sample size used in a study is usually determined based on the cost, time, or convenience of collecting the data, and the need for it to offer sufficient statistical power. In complex studies, different sample sizes may be allocated, such as in stratified surveys or experimental designs with multiple treatment groups. In a census, data is sought for an entire population, hence the intended sample size is equal to the population. In experimental design, where a study may be divided into different treatment groups, there may be different sample sizes for each group.
Robust statistics are statistics that maintain their properties even if the underlying distributional assumptions are incorrect. Robust statistical methods have been developed for many common problems, such as estimating location, scale, and regression parameters. One motivation is to produce statistical methods that are not unduly affected by outliers. Another motivation is to provide methods with good performance when there are small departures from a parametric distribution. For example, robust methods work well for mixtures of two normal distributions with different standard deviations; under this model, non-robust methods like a t-test work poorly.
In statistics, resampling is the creation of new samples based on one observed sample. Resampling methods are:
- Permutation tests
- Bootstrapping
- Cross validation
- Jackknife
A cost estimate is the approximation of the cost of a program, project, or operation. The cost estimate is the product of the cost estimating process. The cost estimate has a single total value and may have identifiable component values.
Bootstrapping is a procedure for estimating the distribution of an estimator by resampling one's data or a model estimated from the data. Bootstrapping assigns measures of accuracy to sample estimates. This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods.
In statistics, shrinkage is the reduction in the effects of sampling variation. In regression analysis, a fitted relationship appears to perform less well on a new data set than on the data set used for fitting. In particular the value of the coefficient of determination 'shrinks'. This idea is complementary to overfitting and, separately, to the standard adjustment made in the coefficient of determination to compensate for the subjective effects of further sampling, like controlling for the potential of new explanatory terms improving the model by chance: that is, the adjustment formula itself provides "shrinkage." But the adjustment formula yields an artificial shrinkage.
In statistics, the bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. In statistics, "bias" is an objective property of an estimator. Bias is a distinct concept from consistency: consistent estimators converge in probability to the true value of the parameter, but may be biased or unbiased.
In statistics and in particular statistical theory, unbiased estimation of a standard deviation is the calculation from a statistical sample of an estimated value of the standard deviation of a population of values, in such a way that the expected value of the calculation equals the true value. Except in some important situations, outlined later, the task has little relevance to applications of statistics since its need is avoided by standard procedures, such as the use of significance tests and confidence intervals, or by using Bayesian analysis.
In statistical signal processing, the goal of spectral density estimation (SDE) or simply spectral estimation is to estimate the spectral density of a signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal. One purpose of estimating the spectral density is to detect any periodicities in the data, by observing peaks at the frequencies corresponding to these periodicities.
In various science/engineering applications, such as independent component analysis, image analysis, genetic analysis, speech recognition, manifold learning, and time delay estimation it is useful to estimate the differential entropy of a system or process, given some observations.
In statistics, the mean signed difference (MSD), also known as mean signed deviation, mean signed error, or mean bias error is a sample statistic that summarizes how well a set of estimates match the quantities that they are supposed to estimate. It is one of a number of statistics that can be used to assess an estimation procedure, and it would often be used in conjunction with a sample version of the mean square error.



