
Topography is the study of the forms and features of land surfaces. The topography of an area may refer to the land forms and features themselves, or a description or depiction in maps.
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to a laminar flow, which occurs when a fluid flows in parallel layers, with no disruption between those layers.

Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests.
Modular programming is a software design technique that emphasizes separating the functionality of a program into independent, interchangeable modules, such that each contains everything necessary to execute only one aspect of the desired functionality.
Particle image velocimetry (PIV) is an optical method of flow visualization used in education and research. It is used to obtain instantaneous velocity measurements and related properties in fluids. The fluid is seeded with tracer particles which, for sufficiently small particles, are assumed to faithfully follow the flow dynamics. The fluid with entrained particles is illuminated so that particles are visible. The motion of the seeding particles is used to calculate speed and direction of the flow being studied.

Crystallization is the process by which solid forms, where the atoms or molecules are highly organized into a structure known as a crystal. Some ways by which crystals form are precipitating from a solution, freezing, or more rarely deposition directly from a gas. Attributes of the resulting crystal depend largely on factors such as temperature, air pressure, and in the case of liquid crystals, time of fluid evaporation.

Velocimetry is the measurement of the velocity of fluids. This is a task often taken for granted, and involves far more complex processes than one might expect. It is often used to solve fluid dynamics problems, study fluid networks, in industrial and process control applications, as well as in the creation of new kinds of fluid flow sensors. Methods of velocimetry include particle image velocimetry and particle tracking velocimetry, Molecular tagging velocimetry, laser-based interferometry, ultrasonic Doppler methods, Doppler sensors, and new signal processing methodologies.
The hyporheic zone is the region of sediment and porous space beneath and alongside a stream bed, where there is mixing of shallow groundwater and surface water. The flow dynamics and behavior in this zone is recognized to be important for surface water/groundwater interactions, as well as fish spawning, among other processes. As an innovative urban water management practice, the hyporheic zone can be designed by engineers and actively managed for improvements in both water quality and riparian habitat.

Particle tracking velocimetry (PTV) is a velocimetry method i.e. a technique to measure velocities and trajectories of moving objects. In fluid mechanics research these objects are neutrally buoyant particles that are suspended in fluid flow. As the name suggests, individual particles are tracked, so this technique is a Lagrangian approach, in contrast to particle image velocimetry (PIV), which is an Eulerian method that measures the velocity of the fluid as it passes the observation point, that is fixed in space. There are two experimental PTV methods:

In fluid dynamics, eddy diffusion, eddy dispersion, or turbulent diffusion is a process by which fluid substances mix together due to eddy motion. These eddies can vary widely in size, from subtropical ocean gyres down to the small Kolmogorov microscales, and occur as a result of turbulence. The theory of eddy diffusion was first developed by Sir Geoffrey Ingram Taylor.

Geodynamics is a subfield of geophysics dealing with dynamics of the Earth. It applies physics, chemistry and mathematics to the understanding of how mantle convection leads to plate tectonics and geologic phenomena such as seafloor spreading, mountain building, volcanoes, earthquakes, faulting. It also attempts to probe the internal activity by measuring magnetic fields, gravity, and seismic waves, as well as the mineralogy of rocks and their isotopic composition. Methods of geodynamics are also applied to exploration of other planets.

A flow tracer is any fluid property used to track the flow velocity and circulation patterns. Tracers can be chemical properties, such as radioactive material, or chemical compounds, physical properties, such as density, temperature, salinity, or dyes, and can be natural or artificially induced. Flow tracers are used in many fields, such as physics, hydrology, limnology, oceanography, environmental studies and atmospheric studies.

The interaction between erosion and tectonics has been a topic of debate since the early 1990s. While the tectonic effects on surface processes such as erosion have long been recognized, the opposite has only recently been addressed. The primary questions surrounding this topic are what types of interactions exist between erosion and tectonics and what are the implications of these interactions. While this is still a matter of debate, one thing is clear, Earth's landscape is a product of two factors: tectonics, which can create topography and maintain relief through surface and rock uplift, and climate, which mediates the erosional processes that wear away upland areas over time. The interaction of these processes can form, modify, or destroy geomorphic features on Earth's surface.

A bedform is a geological feature that develops at the interface of fluid and a moveable bed, the result of bed material being moved by fluid flow. Examples include ripples and dunes on the bed of a river. Bedforms are often preserved in the rock record as a result of being present in a depositional setting. Bedforms are often characteristic to the flow parameters, and may be used to infer flow depth and velocity, and therefore the Froude number.

Lagrangian coherent structures (LCSs) are distinguished surfaces of trajectories in a dynamical system that exert a major influence on nearby trajectories over a time interval of interest. The type of this influence may vary, but it invariably creates a coherent trajectory pattern for which the underlying LCS serves as a theoretical centerpiece. In observations of tracer patterns in nature, one readily identifies coherent features, but it is often the underlying structure creating these features that is of interest.

In chaos theory and fluid dynamics, chaotic mixing is a process by which flow tracers develop into complex fractals under the action of a fluid flow. The flow is characterized by an exponential growth of fluid filaments. Even very simple flows, such as the blinking vortex, or finitely resolved wind fields can generate exceptionally complex patterns from initially simple tracer fields.
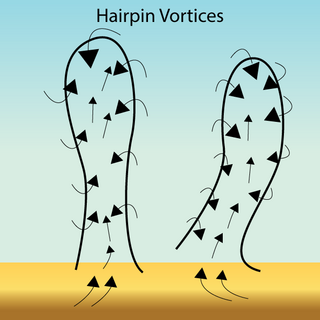
Turbulent flows are complex multi-scale and chaotic motions that need to be classified into more elementary components, referred to coherent turbulent structures. Such a structure must have temporal coherence, i.e. it must persist in its form for long enough periods that the methods of time-averaged statistics can be applied. Coherent structures are typically studied on very large scales, but can be broken down into more elementary structures with coherent properties of their own, such examples include hairpin vortices. Hairpins and coherent structures have been studied and noticed in data since the 1930s, and have been since cited in thousands of scientific papers and reviews.
Lagrangian ocean analysis is a way of analysing ocean dynamics by computing the trajectories of virtual fluid particles, following the Lagrangian perspective of fluid flow, from a specified velocity field. Often, the Eulerian velocity field used as an input for Lagrangian ocean analysis has been computed using an ocean general circulation model (OGCM). Lagrangian techniques can be employed on a range of scales, from modelling the dispersal of biological matter within the Great Barrier Reef to global scales. Lagrangian ocean analysis has numerous applications, from modelling the diffusion of tracers, through the dispersal of aircraft debris and plastics, to determining the biological connectivity of ocean regions.
OceanParcels, “Probably A Really Computationally Efficient Lagrangian Simulator”, is a set of python classes and methods that is used to track particles like water, plankton and plastics. It uses the output of Ocean General Circulation Models (OGCM's). OceanParcels main goal is to process the increasingly large amounts of data that is governed by OGCM's. The flow dynamics are simulated using Lagrangian modelling and the geophysical fluid dynamics are simulated with Eulerian modelling or provided through experimental data. OceanParcels is dependent on two principles, namely the ability to read external data sets from different formats and customizable kernels to define particle dynamics.











