F26A graph

F26A graph
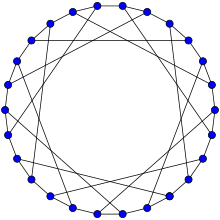	The F26A graph is Hamiltonian.
Vertices	26
Edges	39
Radius	5
Diameter	5
Girth	6
Automorphisms	78 (C13⋊C6)
Chromatic number	2
Chromatic index	3
Properties	Cayley graph ; Symmetric ; Cubic ; Hamiltonian [1]
	Table of graphs and parameters

Last updated August 25, 2019

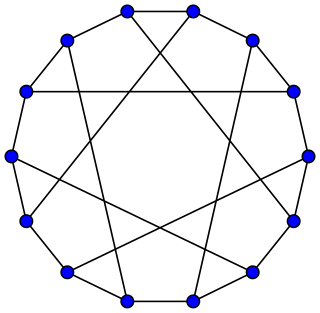
In the mathematical field of graph theory, the F26A graph is a symmetric bipartite cubic graph with 26 vertices and 39 edges.^[1]

Mathematics Field of study concerning quantity, patterns and change

Mathematics includes the study of such topics as quantity, structure (algebra), space (geometry), and change. It has no generally accepted definition.

Graph theory Area of discrete mathematics

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically; see Graph for more detailed definitions and for other variations in the types of graph that are commonly considered. Graphs are one of the prime objects of study in discrete mathematics.

In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u₁—v₁ and u₂—v₂ of G, there is an automorphism

In graph theory, the girth of a graph is the length of a shortest cycle contained in the graph. If the graph does not contain any cycles, its girth is defined to be infinity. For example, a 4-cycle (square) has girth 4. A grid has girth 4 as well, and a triangular mesh has girth 3. A graph with girth four or more is triangle-free.

In graph theory, a connected graph G is said to be k-vertex-connected if it has more than k vertices and remains connected whenever fewer than k vertices are removed.

In graph theory, a connected graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.

The F26A graph is Hamiltonian and can be described by the LCF notation [−7, 7]¹³.

In combinatorial mathematics, LCF notation or LCF code is a notation devised by Joshua Lederberg, and extended by H. S. M. Coxeter and Robert Frucht, for the representation of cubic graphs that contain a Hamiltonian cycle. The cycle itself includes two out of the three adjacencies for each vertex, and the LCF notation specifies how far along the cycle each vertex's third neighbor is. A single graph may have multiple different representations in LCF notation.

Algebraic properties

The automorphism group of the F26A graph is a group of order 78.^[3] It acts transitively on the vertices, on the edges, and on the arcs of the graph. Therefore, the F26A graph is a symmetric graph (though not distance transitive). It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the F26A graph is the only cubic symmetric graph on 26 vertices.^[2] It is also a Cayley graph for the dihedral group D₂₆, generated by a, ab, and ab⁴, where:^[4]

In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity.

In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y. Distance-transitive graphs were first defined in 1971 by Norman L. Biggs and D. H. Smith.

In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group. It is a central tool in combinatorial and geometric group theory.

D_{26}=\langle a,b|a^{2}=b^{13}=1,aba=b^{-1}\rangle .

The F26A graph is the smallest cubic graph where the automorphism group acts regularly on arcs (that is, on edges considered as having a direction).^[5]

The characteristic polynomial of the F26A graph is equal to

In linear algebra, the characteristic polynomial of a square matrix is a polynomial which is invariant under matrix similarity and has the eigenvalues as roots. It has the determinant and the trace of the matrix as coefficients. The characteristic polynomial of an endomorphism of vector spaces of finite dimension is the characteristic polynomial of the matrix of the endomorphism over any base; it does not depend on the choice of a basis. The characteristic equation is the equation obtained by equating to zero the characteristic polynomial.

(x-3)(x+3)(x^{4}-5x^{2}+3)^{6}.\,

Other properties

The F26A graph can be embedded as a chiral regular map in the torus, with 13 hexagonal faces. The dual graph for this embedding is isomorphic to the Paley graph of order 13.

Gallery

The chromatic number of the F26A graph is 2.
The chromatic index of the F26A graph is 3.
Alternative drawing of the F26A graph.
F26A graph embedded in the torus.

Related Research Articles

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v₁ and v₂ of G, there is some automorphism

In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.

In the mathematical field of graph theory, a semi-symmetric graph is an undirected graph that is edge-transitive and regular, but not vertex-transitive. In other words, a graph is semi-symmetric if each vertex has the same number of incident edges, and there is a symmetry taking any of the graph's edges to any other of its edges, but there is some pair of vertices such that no symmetry maps the first into the second.

In the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 (unpublished), then discovered independently by Bouwer 1968 in reply to a question posed by Jon Folkman 1967. The Gray graph is interesting as the first known example of a cubic graph having the algebraic property of being edge but not vertex transitive.

In the mathematical field of graph theory, the Coxeter graph is a 3-regular graph with 28 vertices and 42 edges. It is one of the 13 cubic distance-regular graphs are known. It is named after Harold Scott MacDonald Coxeter.

In the mathematical field of graph theory, the Pappus graph is a bipartite 3-regular undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is named after Pappus of Alexandria, an ancient Greek mathematician who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the cubic distance-regular graphs are known; the Pappus graph is one of the 13 such graphs.

In the mathematical field of graph theory, the Foster graph is a bipartite 3-regular graph with 90 vertices and 135 edges.

In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor. It can be defined as the generalized Petersen graph G(8,3): that is, it is formed by the vertices of an octagon, connected to the vertices of an eight-point star in which each point of the star is connected to the points three steps away from it.

In the mathematical field of graph theory, the Shrikhande graph is a named graph discovered by S. S. Shrikhande in 1959. It is a strongly regular graph with 16 vertices and 48 edges, with each vertex having degree 6. Every pair of nodes has exactly two other neighbors in common, whether the pair of nodes is connected or not.

In the mathematical field of graph theory, the Franklin graph a 3-regular graph with 12 vertices and 18 edges.

In the mathematical field of graph theory, the Folkman graph, named after Jon Folkman, is a bipartite 4-regular graph with 20 vertices and 40 edges.

In the mathematical field of graph theory, the Biggs–Smith graph is a 3-regular graph with 102 vertices and 153 edges.

In the mathematical field of graph theory, the Dyck graph is a 3-regular graph with 32 vertices and 48 edges, named after Walther von Dyck.

In the mathematical field of graph theory, the Nauru graph is a symmetric bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.

In the mathematical field of graph theory, the Ljubljana graph is an undirected bipartite graph with 112 vertices and 168 edges.

In the mathematical field of graph theory, the Tutte 12-cage or Benson graph is a 3-regular graph with 126 vertices and 189 edges named after W. T. Tutte.

In the mathematical field of graph theory, the Klein graphs are two different but related regular graphs, each with 84 edges. Each can be embedded in the orientable surface of genus 3, in which they form dual graphs.

The 110-vertex Iofinova-Ivanov graph is, in graph theory, a semi-symmetric cubic graph with 110 vertices and 165 edges.

References

1 2 Weisstein, Eric W. "Cubic Symmetric Graph". MathWorld .
1 2 Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41–63, 2002.
↑ Royle, G. F026A data
↑ "Yan-Quan Feng and Jin Ho Kwak, Cubic s-Regular Graphs, p. 67" (PDF). Archived from the original (PDF) on 2006-08-26. Retrieved 2010-03-12.
↑ Yan-Quan Feng and Jin Ho Kwak, "One-regular cubic graphs of order a small number times a prime or a prime square," J. Aust. Math. Soc. 76 (2004), 345-356 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Mathworld-1] 1 2 Weisstein, Eric W. "Cubic Symmetric Graph". MathWorld .

[COND-2] 1 2 Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41–63, 2002.

[3] Royle, G. F026A data

[4] "Yan-Quan Feng and Jin Ho Kwak, Cubic s-Regular Graphs, p. 67" (PDF). Archived from the original (PDF) on 2006-08-26. Retrieved 2010-03-12.

[5] Yan-Quan Feng and Jin Ho Kwak, "One-regular cubic graphs of order a small number times a prime or a prime square," J. Aust. Math. Soc. 76 (2004), 345-356 .