In computational mathematics, an iterative method is a mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the n-th approximation is derived from the previous ones.

The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves or electromagnetic waves. It arises in fields like acoustics, electromagnetism, and fluid dynamics.

The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In mathematics, an eigenfunction of a linear operator D defined on some function space is any non-zero function in that space that, when acted upon by D, is only multiplied by some scaling factor called an eigenvalue. As an equation, this condition can be written as
In numerical linear algebra, the method of successive over-relaxation (SOR) is a variant of the Gauss–Seidel method for solving a linear system of equations, resulting in faster convergence. A similar method can be used for any slowly converging iterative process.
An eikonal equation is a non-linear first-order partial differential equation that is encountered in problems of wave propagation.
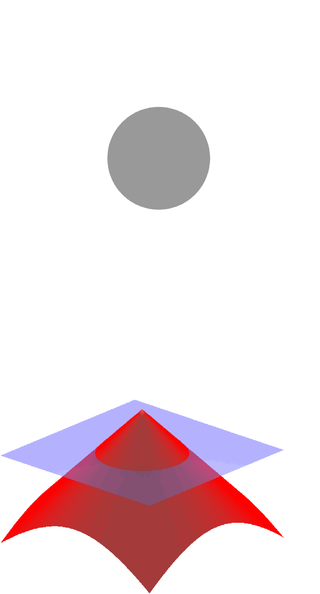
In mathematics and its applications, the signed distance function is the orthogonal distance of a given point x to the boundary of a set Ω in a metric space, with the sign determined by whether or not x is in the interior of Ω. The function has positive values at points x inside Ω, it decreases in value as x approaches the boundary of Ω where the signed distance function is zero, and it takes negative values outside of Ω. However, the alternative convention is also sometimes taken instead.

The Navier–Stokes existence and smoothness problem concerns the mathematical properties of solutions to the Navier–Stokes equations, a system of partial differential equations that describe the motion of a fluid in space. Solutions to the Navier–Stokes equations are used in many practical applications. However, theoretical understanding of the solutions to these equations is incomplete. In particular, solutions of the Navier–Stokes equations often include turbulence, which remains one of the greatest unsolved problems in physics, despite its immense importance in science and engineering.
The fast marching method is a numerical method created by James Sethian for solving boundary value problems of the Eikonal equation:
Numerical continuation is a method of computing approximate solutions of a system of parameterized nonlinear equations,
In applied mathematics, discontinuous Galerkin methods (DG methods) form a class of numerical methods for solving differential equations. They combine features of the finite element and the finite volume framework and have been successfully applied to hyperbolic, elliptic, parabolic and mixed form problems arising from a wide range of applications. DG methods have in particular received considerable interest for problems with a dominant first-order part, e.g. in electrodynamics, fluid mechanics and plasma physics.
In mathematics, Neumann–Neumann methods are domain decomposition preconditioners named so because they solve a Neumann problem on each subdomain on both sides of the interface between the subdomains. Just like all domain decomposition methods, so that the number of iterations does not grow with the number of subdomains, Neumann–Neumann methods require the solution of a coarse problem to provide global communication. The balancing domain decomposition is a Neumann–Neumann method with a special kind of coarse problem.

The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential.
In fluid dynamics, The projection method is an effective means of numerically solving time-dependent incompressible fluid-flow problems. It was originally introduced by Alexandre Chorin in 1967 as an efficient means of solving the incompressible Navier-Stokes equations. The key advantage of the projection method is that the computations of the velocity and the pressure fields are decoupled.
In the finite element method for the numerical solution of elliptic partial differential equations, the stiffness matrix is a matrix that represents the system of linear equations that must be solved in order to ascertain an approximate solution to the differential equation.
In scientific computation and simulation, the method of fundamental solutions (MFS) is a technique for solving partial differential equations based on using the fundamental solution as a basis function. The MFS was developed to overcome the major drawbacks in the boundary element method (BEM) which also uses the fundamental solution to satisfy the governing equation. Consequently, both the MFS and the BEM are of a boundary discretization numerical technique and reduce the computational complexity by one dimensionality and have particular edge over the domain-type numerical techniques such as the finite element and finite volume methods on the solution of infinite domain, thin-walled structures, and inverse problems.
In numerical mathematics, the boundary knot method (BKM) is proposed as an alternative boundary-type meshfree distance function collocation scheme.
The Kansa method is a computer method used to solve partial differential equations. Its main advantage is it is very easy to understand and program on a computer. It is much less complicated than the finite element method. Another advantage is it works well on multi variable problems. The finite element method is complicated when working with more than 3 space variables and time.
Hongkai Zhao is a Chinese mathematician and Ruth F. DeVarney Distinguished Professor of Mathematics at Duke University. He was formerly the Chancellor's Professor in the Department of Mathematics at the University of California, Irvine. He is known for his work in scientific computing, imaging and numerical analysis, such as the fast sweeping method for Hamilton-Jacobi equation and numerical methods for moving interface problems.

The forward problem of electrocardiology is a computational and mathematical approach to study the electrical activity of the heart through the body surface. The principal aim of this study is to computationally reproduce an electrocardiogram (ECG), which has important clinical relevance to define cardiac pathologies such as ischemia and infarction, or to test pharmaceutical intervention. Given their important functionalities and the relative small invasiveness, the electrocardiography techniques are used quite often as clinical diagnostic tests. Thus, it is natural to proceed to computationally reproduce an ECG, which means to mathematically model the cardiac behaviour inside the body.














