This article needs additional citations for verification .(June 2023) |
The Fermi motion is the quantum motion of nucleons bound inside a nucleus. [1] It was once posited as an explanation for the EMC effect.
This article needs additional citations for verification .(June 2023) |
The Fermi motion is the quantum motion of nucleons bound inside a nucleus. [1] It was once posited as an explanation for the EMC effect.

Enrico Fermi was an Italian and later naturalized American physicist, renowned for being the creator of the world's first nuclear reactor, the Chicago Pile-1, and a member of the Manhattan Project. He has been called the "architect of the nuclear age" and the "architect of the atomic bomb". He was one of very few physicists to excel in both theoretical physics and experimental physics. Fermi was awarded the 1938 Nobel Prize in Physics for his work on induced radioactivity by neutron bombardment and for the discovery of transuranium elements. With his colleagues, Fermi filed several patents related to the use of nuclear power, all of which were taken over by the US government. He made significant contributions to the development of statistical mechanics, quantum theory, and nuclear and particle physics.

The Enrico Fermi Award is a scientific award conferred by the President of the United States. It is awarded to honor scientists of international stature for their lifetime achievement in the development, use, or production of energy. It was established in 1956 by the United States Department of Energy in memorial of Italian physicist Enrico Fermi and his work in the development of nuclear power. The recipient of the award receives $100,000, a certificate signed by the President and the Secretary of Energy, and a gold medal featuring the likeness of Enrico Fermi.
The Fermi level of a solid-state body is the thermodynamic work required to add one electron to the body. It is a thermodynamic quantity usually denoted by µ or EF for brevity. The Fermi level does not include the work required to remove the electron from wherever it came from. A precise understanding of the Fermi level—how it relates to electronic band structure in determining electronic properties; how it relates to the voltage and flow of charge in an electronic circuit—is essential to an understanding of solid-state physics.
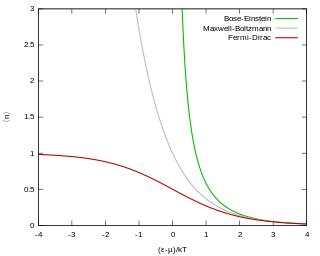
Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926. Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics.
The Fermi energy is a concept in quantum mechanics usually referring to the energy difference between the highest and lowest occupied single-particle states in a quantum system of non-interacting fermions at absolute zero temperature. In a Fermi gas, the lowest occupied state is taken to have zero kinetic energy, whereas in a metal, the lowest occupied state is typically taken to mean the bottom of the conduction band.

A Fermi gas is an idealized model, an ensemble of many non-interacting fermions. Fermions are particles that obey Fermi–Dirac statistics, like electrons, protons, and neutrons, and, in general, particles with half-integer spin. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density, temperature, and the set of available energy states. The model is named after the Italian physicist Enrico Fermi.

Fermi liquid theory is a theoretical model of interacting fermions that describes the normal state of most metals at sufficiently low temperatures. The interactions among the particles of the many-body system do not need to be small. The phenomenological theory of Fermi liquids was introduced by the Soviet physicist Lev Davidovich Landau in 1956, and later developed by Alexei Abrikosov and Isaak Khalatnikov using diagrammatic perturbation theory. The theory explains why some of the properties of an interacting fermion system are very similar to those of the ideal Fermi gas, and why other properties differ.
In physics, screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases, electrolytes, and charge carriers in electronic conductors . In a fluid, with a given permittivity ε, composed of electrically charged constituent particles, each pair of particles interact through the Coulomb force as

Emilio Gino Segrè was an Italian-born American physicist and Nobel laureate, who discovered the elements technetium and astatine, and the antiproton, a subatomic antiparticle, for which he was awarded the Nobel Prize in Physics in 1959 along with Owen Chamberlain.

The Fermi Gamma-ray Space Telescope, formerly called the Gamma-ray Large Area Space Telescope (GLAST), is a space observatory being used to perform gamma-ray astronomy observations from low Earth orbit. Its main instrument is the Large Area Telescope (LAT), with which astronomers mostly intend to perform an all-sky survey studying astrophysical and cosmological phenomena such as active galactic nuclei, pulsars, other high-energy sources and dark matter. Another instrument aboard Fermi, the Gamma-ray Burst Monitor, is being used to study gamma-ray bursts and solar flares.
In solid-state physics, the free electron model is a quantum mechanical model for the behaviour of charge carriers in a metallic solid. It was developed in 1927, principally by Arnold Sommerfeld, who combined the classical Drude model with quantum mechanical Fermi–Dirac statistics and hence it is also known as the Drude–Sommerfeld model.

Chicago Pile-1 (CP-1) was the world's first artificial nuclear reactor. On 2 December 1942, the first human-made self-sustaining nuclear chain reaction was initiated in CP-1 during an experiment led by Enrico Fermi. The secret development of the reactor was the first major technical achievement for the Manhattan Project, the Allied effort to create nuclear weapons during World War II. Developed by the Metallurgical Laboratory at the University of Chicago, CP-1 was built under the west viewing stands of the original Stagg Field. Although the project's civilian and military leaders had misgivings about the possibility of a disastrous runaway reaction, they trusted Fermi's safety calculations and decided they could carry out the experiment in a densely populated area. Fermi described the reactor as "a crude pile of black bricks and wooden timbers".
In physics, the Fermi–Pasta–Ulam–Tsingou (FPUT) problem or formerly the Fermi–Pasta–Ulam problem was the apparent paradox in chaos theory that many complicated enough physical systems exhibited almost exactly periodic behavior – called Fermi–Pasta–Ulam–Tsingou recurrence – instead of the expected ergodic behavior. This came as a surprise, as Enrico Fermi, certainly, expected the system to thermalize in a fairly short time. That is, it was expected for all vibrational modes to eventually appear with equal strength, as per the equipartition theorem, or, more generally, the ergodic hypothesis. Yet here was a system that appeared to evade the ergodic hypothesis. Although the recurrence is easily observed, it eventually became apparent that over much, much longer time periods, the system does eventually thermalize. Multiple competing theories have been proposed to explain the behavior of the system, and it remains a topic of active research.

Orso Mario Corbino was an Italian physicist and politician. He is noted for his studies of the influence of external magnetic fields on the motion of electrons in metals and he discovered the Corbino effect. He served as the minister for education in 1921 and as the Minister for National Economy in 1921. He also served as professor of the University of Messina (1905) and of the University of Rome (1908).

In solid-state physics of semiconductors, a band diagram is a diagram plotting various key electron energy levels as a function of some spatial dimension, which is often denoted x. These diagrams help to explain the operation of many kinds of semiconductor devices and to visualize how bands change with position. The bands may be coloured to distinguish level filling.
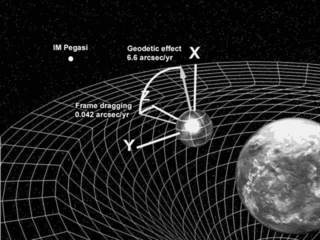
The geodetic effect represents the effect of the curvature of spacetime, predicted by general relativity, on a vector carried along with an orbiting body. For example, the vector could be the angular momentum of a gyroscope orbiting the Earth, as carried out by the Gravity Probe B experiment. The geodetic effect was first predicted by Willem de Sitter in 1916, who provided relativistic corrections to the Earth–Moon system's motion. De Sitter's work was extended in 1918 by Jan Schouten and in 1920 by Adriaan Fokker. It can also be applied to a particular secular precession of astronomical orbits, equivalent to the rotation of the Laplace–Runge–Lenz vector.
In the mathematical theory of Riemannian geometry, there are two uses of the term Fermi coordinates. In one use they are local coordinates that are adapted to a geodesic. In a second, more general one, they are local coordinates that are adapted to any world line, even not geodesical.
The Thomas–Fermi (TF) model, named after Llewellyn Thomas and Enrico Fermi, is a quantum mechanical theory for the electronic structure of many-body systems developed semiclassically shortly after the introduction of the Schrödinger equation. It stands separate from wave function theory as being formulated in terms of the electronic density alone and as such is viewed as a precursor to modern density functional theory. The Thomas–Fermi model is correct only in the limit of an infinite nuclear charge. Using the approximation for realistic systems yields poor quantitative predictions, even failing to reproduce some general features of the density such as shell structure in atoms and Friedel oscillations in solids. It has, however, found modern applications in many fields through the ability to extract qualitative trends analytically and with the ease at which the model can be solved. The kinetic energy expression of Thomas–Fermi theory is also used as a component in more sophisticated density approximation to the kinetic energy within modern orbital-free density functional theory.
A proper reference frame in the theory of relativity is a particular form of accelerated reference frame, that is, a reference frame in which an accelerated observer can be considered as being at rest. It can describe phenomena in curved spacetime, as well as in "flat" Minkowski spacetime in which the spacetime curvature caused by the energy–momentum tensor can be disregarded. Since this article considers only flat spacetime—and uses the definition that special relativity is the theory of flat spacetime while general relativity is a theory of gravitation in terms of curved spacetime—it is consequently concerned with accelerated frames in special relativity.