Related Research Articles

Rendering or image synthesis is the process of generating a photorealistic or non-photorealistic image from a 2D or 3D model by means of a computer program. The resulting image is referred to as the render. Multiple models can be defined in a scene file containing objects in a strictly defined language or data structure. The scene file contains geometry, viewpoint, texture, lighting, and shading information describing the virtual scene. The data contained in the scene file is then passed to a rendering program to be processed and output to a digital image or raster graphics image file. The term "rendering" is analogous to the concept of an artist's impression of a scene. The term "rendering" is also used to describe the process of calculating effects in a video editing program to produce the final video output.
A discrete element method (DEM), also called a distinct element method, is any of a family of numerical methods for computing the motion and effect of a large number of small particles. Though DEM is very closely related to molecular dynamics, the method is generally distinguished by its inclusion of rotational degrees-of-freedom as well as stateful contact and often complicated geometries. With advances in computing power and numerical algorithms for nearest neighbor sorting, it has become possible to numerically simulate millions of particles on a single processor. Today DEM is becoming widely accepted as an effective method of addressing engineering problems in granular and discontinuous materials, especially in granular flows, powder mechanics, and rock mechanics. DEM has been extended into the Extended Discrete Element Method taking heat transfer, chemical reaction and coupling to CFD and FEM into account.

Computational physics is the study and implementation of numerical analysis to solve problems in physics for which a quantitative theory already exists. Historically, computational physics was the first application of modern computers in science, and is now a subset of computational science. It is sometimes regarded as a subdiscipline of theoretical physics, but others consider it an intermediate branch between theoretical and experimental physics - an area of study which supplements both theory and experiment.

Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamic "evolution" of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton's equations of motion for a system of interacting particles, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanics force fields. The method is applied mostly in chemical physics, materials science, and biophysics.

A particle system is a technique in game physics, motion graphics, and computer graphics that uses many minute sprites, 3D models, or other graphic objects to simulate certain kinds of "fuzzy" phenomena, which are otherwise very hard to reproduce with conventional rendering techniques – usually highly chaotic systems, natural phenomena, or processes caused by chemical reactions.
Dynamical simulation, in computational physics, is the simulation of systems of objects that are free to move, usually in three dimensions according to Newton's laws of dynamics, or approximations thereof. Dynamical simulation is used in computer animation to assist animators to produce realistic motion, in industrial design, and in video games. Body movement is calculated using time integration methods.

Crowd simulation is the process of simulating the movement of a large number of entities or characters. It is commonly used to create virtual scenes for visual media like films and video games, and is also used in crisis training, architecture and urban planning, and evacuation simulation.

A physics engine is computer software that provides an approximate simulation of certain physical systems, such as rigid body dynamics, soft body dynamics, and fluid dynamics, of use in the domains of computer graphics, video games and film (CGI). Their main uses are in video games, in which case the simulations are in real-time. The term is sometimes used more generally to describe any software system for simulating physical phenomena, such as high-performance scientific simulation.

In the context of chemistry and molecular modelling, a force field is a computational method that is used to estimate the forces between atoms within molecules and also between molecules. More precisely, the force field refers to the functional form and parameter sets used to calculate the potential energy of a system of atoms or coarse-grained particles in molecular mechanics, molecular dynamics, or Monte Carlo simulations. The parameters for a chosen energy function may be derived from experiments in physics and chemistry, calculations in quantum mechanics, or both. Force fields are interatomic potentials and utilize the same concept as force fields in classical physics, with the difference that the force field parameters in chemistry describe the energy landscape, from which the acting forces on every particle are derived as a gradient of the potential energy with respect to the particle coordinates.

Soft-body dynamics is a field of computer graphics that focuses on visually realistic physical simulations of the motion and properties of deformable objects. The applications are mostly in video games and films. Unlike in simulation of rigid bodies, the shape of soft bodies can change, meaning that the relative distance of two points on the object is not fixed. While the relative distances of points are not fixed, the body is expected to retain its shape to some degree. The scope of soft body dynamics is quite broad, including simulation of soft organic materials such as muscle, fat, hair and vegetation, as well as other deformable materials such as clothing and fabric. Generally, these methods only provide visually plausible emulations rather than accurate scientific/engineering simulations, though there is some crossover with scientific methods, particularly in the case of finite element simulations. Several physics engines currently provide software for soft-body simulation.

Fluid–structure interaction (FSI) is the interaction of some movable or deformable structure with an internal or surrounding fluid flow. Fluid–structure interactions can be stable or oscillatory. In oscillatory interactions, the strain induced in the solid structure causes it to move such that the source of strain is reduced, and the structure returns to its former state only for the process to repeat.

In computational chemistry, a water model is used to simulate and thermodynamically calculate water clusters, liquid water, and aqueous solutions with explicit solvent. The models are determined from quantum mechanics, molecular mechanics, experimental results, and these combinations. To imitate a specific nature of molecules, many types of models have been developed. In general, these can be classified by the following three points; (i) the number of interaction points called site, (ii) whether the model is rigid or flexible, (iii) whether the model includes polarization effects.
Stokesian dynamics is a solution technique for the Langevin equation, which is the relevant form of Newton's 2nd law for a Brownian particle. The method treats the suspended particles in a discrete sense while the continuum approximation remains valid for the surrounding fluid, i.e., the suspended particles are generally assumed to be significantly larger than the molecules of the solvent. The particles then interact through hydrodynamic forces transmitted via the continuum fluid, and when the particle Reynolds number is small, these forces are determined through the linear Stokes equations. In addition, the method can also resolve non-hydrodynamic forces, such as Brownian forces, arising from the fluctuating motion of the fluid, and interparticle or external forces. Stokesian Dynamics can thus be applied to a variety of problems, including sedimentation, diffusion and rheology, and it aims to provide the same level of understanding for multiphase particulate systems as molecular dynamics does for statistical properties of matter. For rigid particles of radius suspended in an incompressible Newtonian fluid of viscosity and density , the motion of the fluid is governed by the Navier–Stokes equations, while the motion of the particles is described by the coupled equation of motion:
In computational chemistry, a constraint algorithm is a method for satisfying the Newtonian motion of a rigid body which consists of mass points. A restraint algorithm is used to ensure that the distance between mass points is maintained. The general steps involved are: (i) choose novel unconstrained coordinates, (ii) introduce explicit constraint forces, (iii) minimize constraint forces implicitly by the technique of Lagrange multipliers or projection methods.
Dissipative particle dynamics (DPD) is a stochastic simulation technique for simulating the dynamic and rheological properties of simple and complex fluids. It was initially devised by Hoogerbrugge and Koelman to avoid the lattice artifacts of the so-called lattice gas automata and to tackle hydrodynamic time and space scales beyond those available with molecular dynamics (MD). It was subsequently reformulated and slightly modified by P. Español to ensure the proper thermal equilibrium state. A series of new DPD algorithms with reduced computational complexity and better control of transport properties are presented. The algorithms presented in this article choose randomly a pair particle for applying DPD thermostating thus reducing the computational complexity.
The material point method (MPM) is a numerical technique used to simulate the behavior of solids, liquids, gases, and any other continuum material. Especially, it is a robust spatial discretization method for simulating multi-phase (solid-fluid-gas) interactions. In the MPM, a continuum body is described by a number of small Lagrangian elements referred to as 'material points'. These material points are surrounded by a background mesh/grid that is used only to calculate gradient terms such as the deformation gradient. Unlike other mesh-based methods like the finite element method, finite volume method or finite difference method, the MPM is not a mesh based method and is instead categorized as a meshless/meshfree or continuum-based particle method, examples of which are smoothed particle hydrodynamics and peridynamics. Despite the presence of a background mesh, the MPM does not encounter the drawbacks of mesh-based methods which makes it a promising and powerful tool in computational mechanics.

In physics, the n-body problem is the problem of predicting the individual motions of a group of celestial objects interacting with each other gravitationally. Solving this problem has been motivated by the desire to understand the motions of the Sun, Moon, planets, and visible stars. In the 20th century, understanding the dynamics of globular cluster star systems became an important n-body problem. The n-body problem in general relativity is considerably more difficult to solve due to additional factors like time and space distortions.
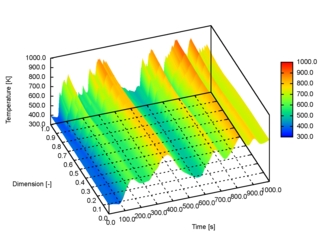
The extended discrete element method (XDEM) is a numerical technique that extends the dynamics of granular material or particles as described through the classical discrete element method (DEM) by additional properties such as the thermodynamic state, stress/strain or electro-magnetic field for each particle. Contrary to a continuum mechanics concept, the XDEM aims at resolving the particulate phase with its various processes attached to the particles. While the discrete element method predicts position and orientation in space and time for each particle, the extended discrete element method additionally estimates properties such as internal temperature and/or species distribution or mechanical impact with structures.
Physically based animation is an area of interest within computer graphics concerned with the simulation of physically plausible behaviors at interactive rates. Advances in physically based animation are often motivated by the need to include complex, physically inspired behaviors in video games, interactive simulations, and movies. Although off-line simulation methods exist to solve most all of the problems studied in physically-based animation, these methods are intended for applications that necessitate physical accuracy and slow, detailed computations. In contrast to methods common in offline simulation, techniques in physically based animation are concerned with physical plausibility, numerical stability, and visual appeal over physical accuracy. Physically based animation is often limited to loose approximations of physical behaviors because of the strict time constraints imposed by interactive applications. The target frame rate for interactive applications such as games and simulations is often 25-60 hertz, with only a small fraction of the time allotted to an individual frame remaining for physical simulation. Simplified models of physical behaviors are generally preferred if they are more efficient, easier to accelerate, or satisfy desirable mathematical properties. Fine details are not important when the overriding goal of a visualization is aesthetic appeal or the maintenance of player immersion since these details are often difficult for humans to notice or are otherwise impossible to distinguish at human scales.
Computational materials science and engineering uses modeling, simulation, theory, and informatics to understand materials. The main goals include discovering new materials, determining material behavior and mechanisms, explaining experiments, and exploring materials theories. It is analogous to computational chemistry and computational biology as an increasingly important subfield of materials science.
References
- ↑ Stockie, John M.; Green, Sheldon I. (1998). "Simulating the Motion of Flexible Pulp Fibres Using the Immersed Boundary Method". Journal of Computational Physics. 147 (1): 147–165. CiteSeerX 10.1.1.33.2125 . doi:10.1006/jcph.1998.6086.
- ↑ Dastan, Alireza; Abouali, Omid; Ahmadi, Goodarz (2014). "CFD simulation of total and regional fiber deposition in human nasal cavities". Journal of Aerosol Science. 69: 132–149. doi:10.1016/j.jaerosci.2013.12.008.
- ↑ Ward, Kelly; Bertails, Florence; Kim, Tae-yong; Marschner, Stephen R.; Cani, Marie-paule; Lin, Ming C. (2007). "A Survey on Hair Modeling: Styling, Simulation, and Rendering". IEEE Transactions on Visualization and Computer Graphics. 13 (2): 213–234. CiteSeerX 10.1.1.132.1734 . doi:10.1109/TVCG.2007.30.
- ↑ Antman, Stuart S. (2005). Nonlinear Problems of Elasticity. Applied Mathematical Sciences. Springer. ISBN 978-0-387-27649-6.