Numerical methods for partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations (PDEs).
The boundary element method (BEM) is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations, including fluid mechanics, acoustics, electromagnetics, fracture mechanics, and contact mechanics.

Finite-difference time-domain (FDTD) or Yee's method is a numerical analysis technique used for modeling computational electrodynamics. Since it is a time-domain method, FDTD solutions can cover a wide frequency range with a single simulation run, and treat nonlinear material properties in a natural way.
Harmonic balance is a method used to calculate the steady-state response of nonlinear differential equations, and is mostly applied to nonlinear electrical circuits. It is a frequency domain method for calculating the steady state, as opposed to the various time-domain steady-state methods. The name "harmonic balance" is descriptive of the method, which starts with Kirchhoff's Current Law written in the frequency domain and a chosen number of harmonics. A sinusoidal signal applied to a nonlinear component in a system will generate harmonics of the fundamental frequency. Effectively the method assumes a linear combination of sinusoids can represent the solution, then balances current and voltage sinusoids to satisfy Kirchhoff's law. The method is commonly used to simulate circuits which include nonlinear elements, and is most applicable to systems with feedback in which limit cycles occur.

Computational electromagnetics (CEM), computational electrodynamics or electromagnetic modeling is the process of modeling the interaction of electromagnetic fields with physical objects and the environment using computers.
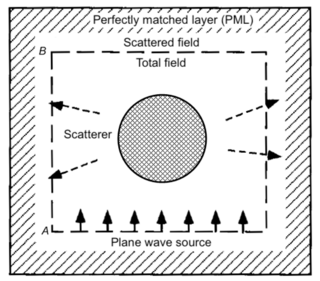
A perfectly matched layer (PML) is an artificial absorbing layer for wave equations, commonly used to truncate computational regions in numerical methods to simulate problems with open boundaries, especially in the FDTD and FE methods. The key property of a PML that distinguishes it from an ordinary absorbing material is that it is designed so that waves incident upon the PML from a non-PML medium do not reflect at the interface—this property allows the PML to strongly absorb outgoing waves from the interior of a computational region without reflecting them back into the interior.
Electromagnetic field solvers are specialized programs that solve Maxwell's equations directly. They form a part of the field of electronic design automation, or EDA, and are commonly used in the design of integrated circuits and printed circuit boards. They are used when a solution from first principles or the highest accuracy is required.
In numerical analysis, finite-difference methods (FDM) are a class of numerical techniques for solving differential equations by approximating derivatives with finite differences. Both the spatial domain and time domain are discretized, or broken into a finite number of intervals, and the values of the solution at the end points of the intervals are approximated by solving algebraic equations containing finite differences and values from nearby points.
Light scattering by particles is the process by which small particles scatter light causing optical phenomena such as the blue color of the sky, and halos.
In computational electromagnetics, the scattering-matrix method (SMM) is a numerical method used to solve Maxwell's equations, related to the transfer-matrix method.
Plane wave expansion method (PWE) refers to a computational technique in electromagnetics to solve the Maxwell's equations by formulating an eigenvalue problem out of the equation. This method is popular among the photonic crystal community as a method of solving for the band structure of specific photonic crystal geometries. PWE is traceable to the analytical formulations, and is useful in calculating modal solutions of Maxwell's equations over an inhomogeneous or periodic geometry. It is specifically tuned to solve problems in a time-harmonic forms, with non-dispersive media.

Finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. Computers are usually used to perform the calculations required. With high-speed supercomputers, better solutions can be achieved and are often required to solve the largest and most complex problems.
In the finite element method for the numerical solution of elliptic partial differential equations, the stiffness matrix is a matrix that represents the system of linear equations that must be solved in order to ascertain an approximate solution to the differential equation.
Miniaturizing components has always been a primary goal in the semiconductor industry because it cuts production cost and lets companies build smaller computers and other devices. Miniaturization, however, has increased dissipated power per unit area and made it a key limiting factor in integrated circuit performance. Temperature increase becomes relevant for relatively small-cross-sections wires, where it may affect normal semiconductor behavior. Besides, since the generation of heat is proportional to the frequency of operation for switching circuits, fast computers have larger heat generation than slow ones, an undesired effect for chips manufacturers. This article summaries physical concepts that describe the generation and conduction of heat in an integrated circuit, and presents numerical methods that model heat transfer from a macroscopic point of view.
Eigenmode expansion (EME) is a computational electrodynamics modelling technique. It is also referred to as the mode matching technique or the bidirectional eigenmode propagation method. Eigenmode expansion is a linear frequency-domain method.
In numerical mathematics, the boundary knot method (BKM) is proposed as an alternative boundary-type meshfree distance function collocation scheme.
The Kansa method is a computer method used to solve partial differential equations. Its main advantage is it is very easy to understand and program on a computer. It is much less complicated than the finite element method. Another advantage is it works well on multi variable problems. The finite element method is complicated when working with more than 3 space variables and time.

A frequency-selective surface (FSS) is any thin, repetitive surface designed to reflect, transmit or absorb electromagnetic fields based on the frequency of the field. In this sense, an FSS is a type of optical filter or metal-mesh optical filters in which the filtering is accomplished by virtue of the regular, periodic pattern on the surface of the FSS. Though not explicitly mentioned in the name, FSSs also have properties which vary with incidence angle and polarization as well; these are unavoidable consequences of the way in which FSSs are constructed. Frequency-selective surfaces have been most commonly used in the radio signals of the electromagnetic spectrum and find use in applications as diverse as the aforementioned microwave oven, antenna radomes and modern metamaterials. Sometimes frequency selective surfaces are referred to simply as periodic surfaces and are a 2-dimensional analog of the new periodic volumes known as photonic crystals.
Kane Shee-Gong Yee is a Chinese-American electrical engineer and mathematician. He is best known for introducing the finite-difference time-domain method (FDTD) in 1966.

The method of moments (MoM), also known as the moment method and method of weighted residuals, is a numerical method in computational electromagnetics. It is used in computer programs that simulate the interaction of electromagnetic fields such as radio waves with matter, for example antenna simulation programs like NEC that calculate the radiation pattern of an antenna. Generally being a frequency-domain method, it involves the projection of an integral equation into a system of linear equations by the application of appropriate boundary conditions. This is done by using discrete meshes as in finite difference and finite element methods, often for the surface. The solutions are represented with the linear combination of pre-defined basis functions; generally, the coefficients of these basis functions are the sought unknowns. Green's functions and Galerkin method play a central role in the method of moments.









