
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced samples of a function into a same-length sequence of equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a complex-valued function of frequency. The interval at which the DTFT is sampled is the reciprocal of the duration of the input sequence. An inverse DFT (IDFT) is a Fourier series, using the DTFT samples as coefficients of complex sinusoids at the corresponding DTFT frequencies. It has the same sample-values as the original input sequence. The DFT is therefore said to be a frequency domain representation of the original input sequence. If the original sequence spans all the non-zero values of a function, its DTFT is continuous, and the DFT provides discrete samples of one cycle. If the original sequence is one cycle of a periodic function, the DFT provides all the non-zero values of one DTFT cycle.

In mathematics, Fourier analysis is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer.
In signal processing, group delay and phase delay are functions that describe in different ways the delay times experienced by a signal’s various sinuoidal frequency components as they pass through a linear time-invariant (LTI) system.

A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing.

In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input and outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term Fourier transform refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches.

In mathematics, Legendre polynomials, named after Adrien-Marie Legendre (1782), are a system of complete and orthogonal polynomials with a wide number of mathematical properties and numerous applications. They can be defined in many ways, and the various definitions highlight different aspects as well as suggest generalizations and connections to different mathematical structures and physical and numerical applications.

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields. The table of spherical harmonics contains a list of common spherical harmonics.
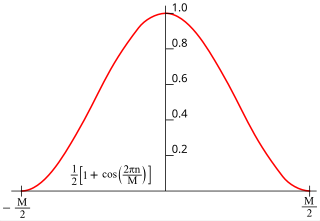
In signal processing and statistics, a window function is a mathematical function that is zero-valued outside of some chosen interval. Typically, window functions are symmetric around the middle of the interval, approach a maximum in the middle, and taper away from the middle. Mathematically, when another function or waveform/data-sequence is "multiplied" by a window function, the product is also zero-valued outside the interval: all that is left is the part where they overlap, the "view through the window". Equivalently, and in actual practice, the segment of data within the window is first isolated, and then only that data is multiplied by the window function values. Thus, tapering, not segmentation, is the main purpose of window functions.
In mathematics, orthogonal functions belong to a function space that is a vector space equipped with a bilinear form. When the function space has an interval as the domain, the bilinear form may be the integral of the product of functions over the interval:
The Daubechies wavelets, based on the work of Ingrid Daubechies, are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments for some given support. With each wavelet type of this class, there is a scaling function which generates an orthogonal multiresolution analysis.

In numerical analysis, Chebyshev nodes are a set of specific real algebraic numbers, used as nodes for polynomial interpolation. They are the projection of equispaced points on the unit circle onto the real interval the diameter of the circle.
In mathematics, the discrete-time Fourier transform (DTFT) is a form of Fourier analysis that is applicable to a sequence of discrete values.
In mathematics, Gegenbauer polynomials or ultraspherical polynomialsC(α)
n(x) are orthogonal polynomials on the interval [−1,1] with respect to the weight function (1 − x2)α–1/2. They generalize Legendre polynomials and Chebyshev polynomials, and are special cases of Jacobi polynomials. They are named after Leopold Gegenbauer.
In electronic music, waveshaping is a type of distortion synthesis in which complex spectra are produced from simple tones by altering the shape of the waveforms.
Clenshaw–Curtis quadrature and Fejér quadrature are methods for numerical integration, or "quadrature", that are based on an expansion of the integrand in terms of Chebyshev polynomials. Equivalently, they employ a change of variables and use a discrete cosine transform (DCT) approximation for the cosine series. Besides having fast-converging accuracy comparable to Gaussian quadrature rules, Clenshaw–Curtis quadrature naturally leads to nested quadrature rules, which is important for both adaptive quadrature and multidimensional quadrature (cubature).
In functional analysis, compactly supported wavelets derived from Legendre polynomials are termed Legendre wavelets or spherical harmonic wavelets. Legendre functions have widespread applications in which spherical coordinate system is appropriate. As with many wavelets there is no nice analytical formula for describing these harmonic spherical wavelets. The low-pass filter associated to Legendre multiresolution analysis is a finite impulse response (FIR) filter.
In mathematics, the discrete Fourier transform over a ring generalizes the discrete Fourier transform (DFT), of a function whose values are commonly complex numbers, over an arbitrary ring.










