Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after L. E. J. (Bertus) Brouwer. It states that for any continuous function mapping a nonempty compact convex set to itself, there is a point such that . The simplest forms of Brouwer's theorem are for continuous functions from a closed interval in the real numbers to itself or from a closed disk to itself. A more general form than the latter is for continuous functions from a nonempty convex compact subset of Euclidean space to itself.

In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space Cn. The existence of a complex derivative in a neighbourhood is a very strong condition: it implies that a holomorphic function is infinitely differentiable and locally equal to its own Taylor series (analytic). Holomorphic functions are the central objects of study in complex analysis.

In complex analysis, the Riemann mapping theorem states that if is a non-empty simply connected open subset of the complex number plane which is not all of , then there exists a biholomorphic mapping from onto the open unit disk

In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally hold for real analytic functions. A function is analytic if and only if its Taylor series about converges to the function in some neighborhood for every in its domain. It is important to note that it is a neighborhood and not just at some point , since every differentiable function has at least a tangent line at every point, which is its Taylor series of order 1. So just having a polynomial expansion at singular points is not enough, and the Taylor series must also converge to the function on points adjacent to to be considered an analytic function. As a counterexample see the Weierstrass function or the Fabius function.

In the mathematical field of complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all of Dexcept for a set of isolated points, which are poles of the function. The term comes from the Greek meros, meaning "part".

In complex analysis, a pole is a certain type of singularity of a complex-valued function of a complex variable. It is the simplest type of non-removable singularity of such a function. Technically, a point z0 is a pole of a function f if it is a zero of the function 1/f and 1/f is holomorphic in some neighbourhood of z0.
In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form
In the mathematical field of complex analysis, a branch point of a multi-valued function is a point such that if the function is n-valued at that point, all of its neighborhoods contain a point that has more than n values. Multi-valued functions are rigorously studied using Riemann surfaces, and the formal definition of branch points employs this concept.
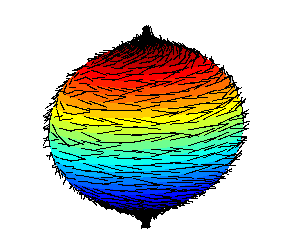
The hairy ball theorem of algebraic topology (sometimes called the hedgehog theorem in Europe) states that there is no nonvanishing continuous tangent vector field on even-dimensional n-spheres. For the ordinary sphere, or 2‑sphere, if f is a continuous function that assigns a vector in R3 to every point p on a sphere such that f(p) is always tangent to the sphere at p, then there is at least one pole, a point where the field vanishes (a p such that f(p) = 0).
In mathematics, the Lefschetz fixed-point theorem is a formula that counts the fixed points of a continuous mapping from a compact topological space to itself by means of traces of the induced mappings on the homology groups of . It is named after Solomon Lefschetz, who first stated it in 1926.
In mathematics, algebraic geometry and analytic geometry are two closely related subjects. While algebraic geometry studies algebraic varieties, analytic geometry deals with complex manifolds and the more general analytic spaces defined locally by the vanishing of analytic functions of several complex variables. The deep relation between these subjects has numerous applications in which algebraic techniques are applied to analytic spaces and analytic techniques to algebraic varieties.
In mathematics, the Atiyah–Bott fixed-point theorem, proven by Michael Atiyah and Raoul Bott in the 1960s, is a general form of the Lefschetz fixed-point theorem for smooth manifolds M, which uses an elliptic complex on M. This is a system of elliptic differential operators on vector bundles, generalizing the de Rham complex constructed from smooth differential forms which appears in the original Lefschetz fixed-point theorem.
Geometric function theory is the study of geometric properties of analytic functions. A fundamental result in the theory is the Riemann mapping theorem.
In mathematics, in the field of algebraic geometry, the period mapping relates families of Kähler manifolds to families of Hodge structures.
In complex analysis, the open mapping theorem states that if U is a domain of the complex plane C and f : U → C is a non-constant holomorphic function, then f is an open map.
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial has a root at a given point is the multiplicity of that root.
In mathematics and in particular the field of complex analysis, Hurwitz's theorem is a theorem associating the zeroes of a sequence of holomorphic, compact locally uniformly convergent functions with that of their corresponding limit. The theorem is named after Adolf Hurwitz.
In mathematics, the Earle–Hamilton fixed point theorem is a result in geometric function theory giving sufficient conditions for a holomorphic mapping of an open domain in a complex Banach space into itself to have a fixed point. The result was proved in 1968 by Clifford Earle and Richard S. Hamilton by showing that, with respect to the Carathéodory metric on the domain, the holomorphic mapping becomes a contraction mapping to which the Banach fixed-point theorem can be applied.
This is a glossary of properties and concepts in algebraic topology in mathematics.
In mathematics, a planar Riemann surface is a Riemann surface sharing the topological properties of a connected open subset of the Riemann sphere. They are characterized by the topological property that the complement of every closed Jordan curve in the Riemann surface has two connected components. An equivalent characterization is the differential geometric property that every closed differential 1-form of compact support is exact. Every simply connected Riemann surface is planar. The class of planar Riemann surfaces was studied by Koebe who proved in 1910, as a generalization of the uniformization theorem, that every such surface is conformally equivalent to either the Riemann sphere or the complex plane with slits parallel to the real axis removed.



