
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity , a number ranging from to .

In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that:
- The orbit of a planet is an ellipse with the Sun at one of the two foci.
- A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.
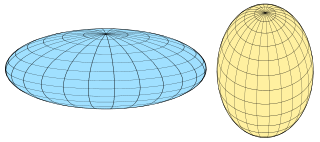
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry.

The orbital period is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. It may also refer to the time it takes a satellite orbiting a planet or moon to complete one orbit.

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
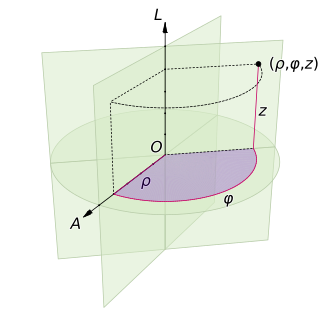
A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions by the distance from a chosen reference axis (axis L in the image opposite), the direction from the axis relative to a chosen reference direction (axis A), and the distance from a chosen reference plane perpendicular to the axis (plane containing the purple section). The latter distance is given as a positive or negative number depending on which side of the reference plane faces the point.

In gravitationally bound systems, the orbital speed of an astronomical body or object is the speed at which it orbits around either the barycenter or, if one body is much more massive than the other bodies of the system combined, its speed relative to the center of mass of the most massive body.

The Gaussian gravitational constant is a parameter used in the orbital mechanics of the Solar System. It relates the orbital period to the orbit's semi-major axis and the mass of the orbiting body in Solar masses.
The Plummer model or Plummer sphere is a density law that was first used by H. C. Plummer to fit observations of globular clusters. It is now often used as toy model in N-body simulations of stellar systems.

In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1. In a wider sense, it is a Kepler orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1.
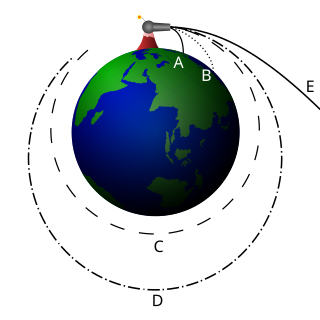
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle. In this case, not only the distance, but also the speed, angular speed, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no radial version.

The Friedmann equations are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity. They were first derived by Alexander Friedmann in 1922 from Einstein's field equations of gravitation for the Friedmann–Lemaître–Robertson–Walker metric and a perfect fluid with a given mass density ρ and pressure p. The equations for negative spatial curvature were given by Friedmann in 1924.
In orbital mechanics, mean motion is the angular speed required for a body to complete one orbit, assuming constant speed in a circular orbit which completes in the same time as the variable speed, elliptical orbit of the actual body. The concept applies equally well to a small body revolving about a large, massive primary body or to two relatively same-sized bodies revolving about a common center of mass. While nominally a mean, and theoretically so in the case of two-body motion, in practice the mean motion is not typically an average over time for the orbits of real bodies, which only approximate the two-body assumption. It is rather the instantaneous value which satisfies the above conditions as calculated from the current gravitational and geometric circumstances of the body's constantly-changing, perturbed orbit.

A gravity train is a theoretical means of transportation for purposes of commuting between two points on the surface of a sphere, by following a straight tunnel connecting the two points through the interior of the sphere.
In physics, the acoustic wave equation is a second-order partial differential equation that governs the propagation of acoustic waves through a material medium resp. a standing wavefield. The equation describes the evolution of acoustic pressure p or particle velocity u as a function of position x and time t. A simplified (scalar) form of the equation describes acoustic waves in only one spatial dimension, while a more general form describes waves in three dimensions. Propagating waves in a pre-defined direction can also be calculated using first order one-way wave equation.

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z). Integrals of a function of two variables over a region in (the real-number plane) are called double integrals, and integrals of a function of three variables over a region in (real-number 3D space) are called triple integrals. For multiple integrals of a single-variable function, see the Cauchy formula for repeated integration.

In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle.

The Sitnikov problem is a restricted version of the three-body problem named after Russian mathematician Kirill Alexandrovitch Sitnikov that attempts to describe the movement of three celestial bodies due to their mutual gravitational attraction. A special case of the Sitnikov problem was first discovered by the American scientist William Duncan MacMillan in 1911, but the problem as it currently stands wasn't discovered until 1961 by Sitnikov.
The Ellis drainhole is the earliest-known complete mathematical model of a traversable wormhole. It is a static, spherically symmetric solution of the Einstein vacuum field equations augmented by inclusion of a scalar field minimally coupled to the geometry of space-time with coupling polarity opposite to the orthodox polarity :
In Einstein's theory of general relativity, the interior Schwarzschild metric is an exact solution for the gravitational field in the interior of a non-rotating spherical body which consists of an incompressible fluid and has zero pressure at the surface. This is a static solution, meaning that it does not change over time. It was discovered by Karl Schwarzschild in 1916, who earlier had found the exterior Schwarzschild metric.




























