Computational chemistry is a branch of chemistry that uses computer simulation to assist in solving chemical problems. It uses methods of theoretical chemistry, incorporated into computer programs, to calculate the structures and properties of molecules, groups of molecules, and solids. It is essential because, apart from relatively recent results concerning the hydrogen molecular ion, the quantum many-body problem cannot be solved analytically, much less in closed form. While computational results normally complement the information obtained by chemical experiments, it can in some cases predict hitherto unobserved chemical phenomena. It is widely used in the design of new drugs and materials.

Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamic "evolution" of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton's equations of motion for a system of interacting particles, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanical force fields. The method is applied mostly in chemical physics, materials science, and biophysics.
Density-functional theory (DFT) is a computational quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using functionals, i.e. functions of another function. In the case of DFT, these are functionals of the spatially dependent electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry.
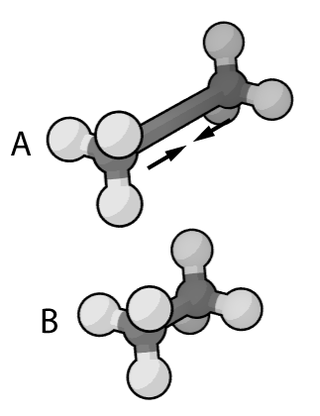
Molecular mechanics uses classical mechanics to model molecular systems. The Born–Oppenheimer approximation is assumed valid and the potential energy of all systems is calculated as a function of the nuclear coordinates using force fields. Molecular mechanics can be used to study molecule systems ranging in size and complexity from small to large biological systems or material assemblies with many thousands to millions of atoms.

Molecular modelling encompasses all methods, theoretical and computational, used to model or mimic the behaviour of molecules. The methods are used in the fields of computational chemistry, drug design, computational biology and materials science to study molecular systems ranging from small chemical systems to large biological molecules and material assemblies. The simplest calculations can be performed by hand, but inevitably computers are required to perform molecular modelling of any reasonably sized system. The common feature of molecular modelling methods is the atomistic level description of the molecular systems. This may include treating atoms as the smallest individual unit, or explicitly modelling protons and neutrons with its quarks, anti-quarks and gluons and electrons with its photons.
Tinker, previously stylized as TINKER, is a suite of computer software applications for molecular dynamics simulation. The codes provide a complete and general set of tools for molecular mechanics and molecular dynamics, with some special features for biomolecules. The core of the software is a modular set of callable routines which allow manipulating coordinates and evaluating potential energy and derivatives via straightforward means.
Car–Parrinello molecular dynamics or CPMD refers to either a method used in molecular dynamics or the computational chemistry software package used to implement this method.
In computational chemistry, a constraint algorithm is a method for satisfying the Newtonian motion of a rigid body which consists of mass points. A restraint algorithm is used to ensure that the distance between mass points is maintained. The general steps involved are: (i) choose novel unconstrained coordinates, (ii) introduce explicit constraint forces, (iii) minimize constraint forces implicitly by the technique of Lagrange multipliers or projection methods.

Umbrella sampling is a technique in computational physics and chemistry, used to improve sampling of a system where ergodicity is hindered by the form of the system's energy landscape. It was first suggested by Torrie and Valleau in 1977. It is a particular physical application of the more general importance sampling in statistics.
The hybrid QM/MM approach is a molecular simulation method that combines the strengths of ab initio QM calculations (accuracy) and MM (speed) approaches, thus allowing for the study of chemical processes in solution and in proteins. The QM/MM approach was introduced in the 1976 paper of Warshel and Levitt. They, along with Martin Karplus, won the 2013 Nobel Prize in Chemistry for "the development of multiscale models for complex chemical systems".
In the field of computational chemistry, energy minimization is the process of finding an arrangement in space of a collection of atoms where, according to some computational model of chemical bonding, the net inter-atomic force on each atom is acceptably close to zero and the position on the potential energy surface (PES) is a stationary point. The collection of atoms might be a single molecule, an ion, a condensed phase, a transition state or even a collection of any of these. The computational model of chemical bonding might, for example, be quantum mechanics.
Thermodynamic integration is a method used to compare the difference in free energy between two given states whose potential energies and have different dependences on the spatial coordinates. Because the free energy of a system is not simply a function of the phase space coordinates of the system, but is instead a function of the Boltzmann-weighted integral over phase space, the free energy difference between two states cannot be calculated directly from the potential energy of just two coordinate sets. In thermodynamic integration, the free energy difference is calculated by defining a thermodynamic path between the states and integrating over ensemble-averaged enthalpy changes along the path. Such paths can either be real chemical processes or alchemical processes. An example alchemical process is the Kirkwood's coupling parameter method.
Desmond is a software package developed at D. E. Shaw Research to perform high-speed molecular dynamics simulations of biological systems on conventional computer clusters. The code uses novel parallel algorithms and numerical methods to achieve high performance on platforms containing multiple processors, but may also be executed on a single computer.
Biochemical and Organic Simulation System (BOSS) is a general-purpose molecular modeling program that performs molecular mechanics calculations, Metropolis Monte Carlo statistical mechanics simulations, and semiempirical Austin Model 1 (AM1), PM3, and PDDG/PM3 quantum mechanics calculations. The molecular mechanics calculations cover energy minimizations, normal mode analysis and conformational searching with the Optimized Potentials for Liquid Simulations (OPLS) force fields. BOSS is developed by Prof. William L. Jorgensen at Yale University, and distributed commercially by Cemcomco, LLC and Schrödinger, Inc.
Local elevation is a technique used in computational chemistry or physics, mainly in the field of molecular simulation. It was developed in 1994 by Huber, Torda and van Gunsteren to enhance the searching of conformational space in molecular dynamics simulations and is available in the GROMOS software for molecular dynamics simulation. The method was, together with the conformational flooding method, the first to introduce memory dependence into molecular simulations. Many recent methods build on the principles of the local elevation technique, including the Engkvist-Karlström, adaptive biasing force, Wang–Landau, metadynamics, adaptively biased molecular dynamics, adaptive reaction coordinate forces, and local elevation umbrella sampling methods. The basic principle of the method is to add a memory-dependent potential energy term in the simulation so as to prevent the simulation to revisit already sampled configurations, which leads to the increased probability of discovering new configurations. The method can be seen as a continuous variant of the Tabu search method.

Newton-X is a general program for molecular dynamics simulations beyond the Born-Oppenheimer approximation. It has been primarily used for simulations of ultrafast processes in photoexcited molecules. It has also been used for simulation of band envelops of absorption and emission spectra.

In theoretical chemistry, the Empirical Valence Bond (EVB) approach is an approximation for calculating free-energies of a chemical reaction in condensed-phase. It was first developed by Israeli chemist Arieh Warshel, and was inspired by the way Marcus theory uses potential surfaces to calculate the probability of electron transfer.
Q is a computer software package for molecular dynamics (MD) simulation. Unlike other MD codes, it has specialized since its conception on three specific types of free energy calculations. These calculations are based on the methods: empirical valence bond (EVB), free energy perturbation (FEP), and linear interaction energy (LIE), as well as, more recently, also path integral calculations using the bisection quantum classical path (BQCP) approach.
In computational chemistry, a solvent model is a computational method that accounts for the behavior of solvated condensed phases. Solvent models enable simulations and thermodynamic calculations applicable to reactions and processes which take place in solution. These include biological, chemical and environmental processes. Such calculations can lead to new predictions about the physical processes occurring by improved understanding.

Dr. Dan Thomas Major is a Professor of Chemistry at Bar Ilan University specializing in Computational Chemistry.







