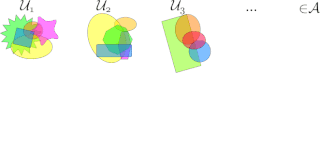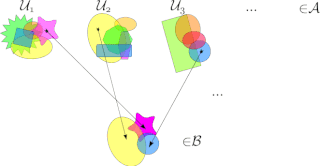Free regular set

Last updated April 02, 2019

In mathematics, a free regular set is a subset of a topological space that is acted upon disjointly under a given group action.^[1]

Mathematics Field of study concerning quantity, patterns and change

Mathematics includes the study of such topics as quantity, structure, space, and change.

In topology and related branches of mathematics, a topological space may be defined as a set of points, along with a set of neighbourhoods for each point, satisfying a set of axioms relating points and neighbourhoods. The definition of a topological space relies only upon set theory and is the most general notion of a mathematical space that allows for the definition of concepts such as continuity, connectedness, and convergence. Other spaces, such as manifolds and metric spaces, are specializations of topological spaces with extra structures or constraints. Being so general, topological spaces are a central unifying notion and appear in virtually every branch of modern mathematics. The branch of mathematics that studies topological spaces in their own right is called point-set topology or general topology.

In mathematics, a group action is a formal way of interpreting the manner in which the elements of a group correspond to transformations of some space in a way that preserves the structure of that space. Common examples of spaces that groups act on are sets, vector spaces, and topological spaces. Actions of groups on vector spaces are called representations of the group.

To be more precise, let X be a topological space. Let G be a group of homeomorphisms from X to X. Then we say that the action of the group G at a point $x\in X$ is freely discontinuous if there exists a neighborhood U of x such that $g(U)\cap U=\varnothing$ for all $g\in G$ , excluding the identity. Such a U is sometimes called a nice neighborhood of x.

Homeomorphism type of mathematical function

In the mathematical field of topology, a homeomorphism, topological isomorphism, or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. The word homeomorphism comes from the Greek words ὅμοιος (homoios) = similar or same and μορφή (morphē) = shape, form, introduced to mathematics by Henri Poincaré in 1895.

In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. It is closely related to the concepts of open set and interior. Intuitively speaking, a neighbourhood of a point is a set of points containing that point where one can move some amount in any direction away from that point without leaving the set.

The set of points at which G is freely discontinuous is called the free regular set and is sometimes denoted by $\Omega =\Omega (G)$ . Note that $\Omega$ is an open set.

In mathematics, and more specifically in topology, an open set is an abstract concept generalizing the idea of an open interval in the real line. The simplest example is in metric spaces, where open sets can be defined as those sets which contain a ball around each of their points ; however, an open set, in general, can be very abstract: any collection of sets can be called open, as long as the union of an arbitrary number of open sets is open, the intersection of a finite number of open sets is open, and the space itself is open. These conditions are very loose, and they allow enormous flexibility in the choice of open sets. In the two extremes, every set can be open, or no set can be open but the space itself and the empty set.

If Y is a subset of X, then Y/G is the space of equivalence classes, and it inherits the canonical topology from Y; that is, the projection from Y to Y/G is continuous and open.

Note that $\Omega /G$ is a Hausdorff space.

In topology and related branches of mathematics, a Hausdorff space, separated space or T₂ space is a topological space where for any two distinct points there exists a neighbourhood of each which is disjoint from the neighbourhood of the other. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" (T₂) is the most frequently used and discussed. It implies the uniqueness of limits of sequences, nets, and filters.

Examples

The open set

\Omega (\Gamma )=\{\tau \in H:|\tau |>1,|\tau +{\overline {\tau }}|<1\}

is the free regular set of the modular group $\Gamma$ on the upper half-plane H. This set is called the fundamental domain on which modular forms are studied.

In mathematics, the modular group is the projective special linear group PSL(2,Z) of 2 x 2 matrices with integer coefficients and unit determinant. The matrices A and -A are identified. The modular group acts on the upper-half of the complex plane by fractional linear transformations, and the name "modular group" comes from the relation to moduli spaces and not from modular arithmetic.

In mathematics, the upper half-plane $H$ is the set of points $(x, y)$ in the Cartesian plane with $y$ > 0.

Given a topological space and a group acting on it, the images of a single point under the group action form an orbit of the action. A fundamental domain or fundamental region is a subset of the space which contains exactly one point from each of these orbits. It serves as a geometric realization for the abstract set of representatives of the orbits.

Related Research Articles

In mathematics, a continuous function is a function for which sufficiently small changes in the input result in arbitrarily small changes in the output. Otherwise, a function is said to be a discontinuous function. A continuous function with a continuous inverse function is called a homeomorphism.

In mathematics, general topology is the branch of topology that deals with the basic set-theoretic definitions and constructions used in topology. It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology. Another name for general topology is point-set topology.

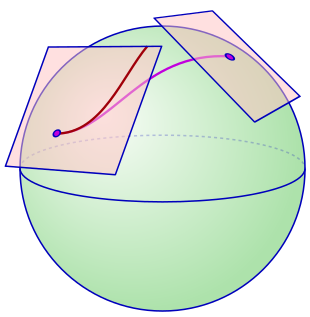
In the branch of mathematics called differential geometry, an affine connection is a geometric object on a smooth manifold which connects nearby tangent spaces, so it permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space. The notion of an affine connection has its roots in 19th-century geometry and tensor calculus, but was not fully developed until the early 1920s, by Élie Cartan and Hermann Weyl. The terminology is due to Cartan and has its origins in the identification of tangent spaces in Euclidean space $R n$ by translation: the idea is that a choice of affine connection makes a manifold look infinitesimally like Euclidean space not just smoothly, but as an affine space.

Bosonic string theory is the original version of string theory, developed in the late 1960s. It is so called because it only contains bosons in the spectrum.

In number theory and algebraic geometry, a modular curveY(Γ) is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL(2, Z). The term modular curve can also be used to refer to the compactified modular curvesX(Γ) which are compactifications obtained by adding finitely many points to this quotient. The points of a modular curve parametrize isomorphism classes of elliptic curves, together with some additional structure depending on the group Γ. This interpretation allows one to give a purely algebraic definition of modular curves, without reference to complex numbers, and, moreover, prove that modular curves are defined either over the field Q of rational numbers, or a cyclotomic field. The latter fact and its generalizations are of fundamental importance in number theory.

In mathematics, the Hamilton–Jacobi equation (HJE) is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations, and is a special case of the Hamilton–Jacobi–Bellman equation. It is named for William Rowan Hamilton and Carl Gustav Jacob Jacobi.

The Havriliak–Negami relaxation is an empirical modification of the Debye relaxation model in electromagnetism. Unlike the Debye model, the Havriliak–Negami relaxation accounts for the asymmetry and broadness of the dielectric dispersion curve. The model was first used to describe the dielectric relaxation of some polymers, by adding two exponential parameters to the Debye equation:

In mathematics, the Gateaux differential or Gateaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gateaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector spaces such as Banach spaces. Like the Fréchet derivative on a Banach space, the Gateaux differential is often used to formalize the functional derivative commonly used in the calculus of variations and physics.

In those branches of mathematics called dynamical systems and ergodic theory, the concept of a wandering set formalizes a certain idea of movement and mixing in such systems. When a dynamical system has a wandering set of non-zero measure, then the system is a dissipative system. This is very much the opposite of a conservative system, for which the ideas of the Poincaré recurrence theorem apply. Intuitively, the connection between wandering sets and dissipation is easily understood: if a portion of the phase space "wanders away" during normal time-evolution of the system, and is never visited again, then the system is dissipative. The language of wandering sets can be used to give a precise, mathematical definition to the concept of a dissipative system. The notion of wandering sets in phase space was introduced by Birkhoff in 1927.

In mathematics, a metric connection is a connection in a vector bundle E equipped with a bundle metric; that is, a metric for which the inner product of any two vectors will remain the same when those vectors are parallel transported along any curve. Other common equivalent formulations of a metric connection include:

In mathematics, in the field of algebraic geometry, the period mapping relates families of Kähler manifolds to families of Hodge structures.

In mathematics, a commutation theorem explicitly identifies the commutant of a specific von Neumann algebra acting on a Hilbert space in the presence of a trace. The first such result was proved by F.J. Murray and John von Neumann in the 1930s and applies to the von Neumann algebra generated by a discrete group or by the dynamical system associated with a measurable transformation preserving a probability measure. Another important application is in the theory of unitary representations of unimodular locally compact groups, where the theory has been applied to the regular representation and other closely related representations. In particular this framework led to an abstract version of the Plancherel theorem for unimodular locally compact groups due to Irving Segal and Forrest Stinespring and an abstract Plancherel theorem for spherical functions associated with a Gelfand pair due to Roger Godement. Their work was put in final form in the 1950s by Jacques Dixmier as part of the theory of Hilbert algebras. It was not until the late 1960s, prompted partly by results in algebraic quantum field theory and quantum statistical mechanics due to the school of Rudolf Haag, that the more general non-tracial Tomita–Takesaki theory was developed, heralding a new era in the theory of von Neumann algebras.

Metal-mesh optical filters are optical filters made from stacks of metal meshes and dielectric. They are used as part of an optical path to filter the incoming light to allow frequencies of interest to pass while reflecting other frequencies of light.

In mathematics, the elliptic modular lambda function λ(τ) is a highly symmetric holomorphic function on the complex upper half-plane. It is invariant under the fractional linear action of the congruence group Γ(2), and generates the function field of the corresponding quotient, i.e., it is a Hauptmodul for the modular curve X(2). Over any point τ, its value can be described as a cross ratio of the branch points of a ramified double cover of the projective line by the elliptic curve $, where the map is defined as the quotient by the [-1] involution.$

In mathematics, a linear map is a mapping $V \to W$ between two modules that preserves the operations of addition and scalar multiplication.

In mathematics, a polyadic space is a topological space that is the image under a continuous function of a topological power of an Alexandroff one-point compactification of a discrete topological space.

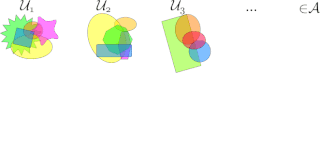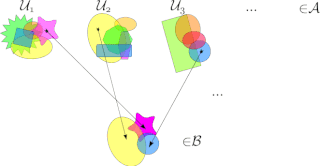
In mathematics, a selection principle is a rule asserting the possibility of obtaining mathematically significant objects by selecting elements from given sequences of sets. The theory of selection principles studies these principles and their relations to other mathematical properties. Selection principles mainly describe covering properties, measure- and category-theoretic properties, and local properties in topological spaces, especially function spaces. Often, the characterization of a mathematical property using a selection principle is a nontrivial task leading to new insights on the characterized property.

In mathematics, Topological Recursion is a recursive definition of invariants of spectral curves. It has applications in enumerative geometry, random matrix theory, mathematical physics, string theory, knot theory.

In mathematics, a $-space$ is a topological space that satisfies a certain a basic selection principle. An infinite cover of a topological space is an $-cover if every finite subset of this space is contained in some member of the cover, and the whole space is not a member the cover. A cover of a topological space is a -cover if every point of this space belongs to all but finitely many members of this cover. A -space is a space in which for every open -cover contains a -cover.$

References

↑ Maskit, Bernard (1987). Discontinuous Groups in the Plane, Grundlehren der mathematischen Wissenschaften Volume 287. Springer Berlin Heidelberg. pp. 15–16. ISBN 978-3-642-64878-6.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Maskit1987-1] Maskit, Bernard (1987). Discontinuous Groups in the Plane, Grundlehren der mathematischen Wissenschaften Volume 287. Springer Berlin Heidelberg. pp. 15–16. ISBN 978-3-642-64878-6.

Free regular set

Contents

Examples

See also

Related Research Articles

References