Game without a value

Last updated September 10, 2022

In the mathematical theory of games, in particular the study of zero-sum continuous games, not every game has a minimax value. This is the expected value to one of the players when both play a perfect strategy (which is to choose from a particular PDF).

The game

Players I and II choose numbers $x$ and $y$ respectively, between 0 and 1. The payoff to player I is

K(x,y)={\begin{cases}-1&{\text{if }}x<y<x+1/2,\\0&{\text{if }}x=y{\text{ or }}y=x+1/2,\\1&{\text{otherwise.}}\end{cases}}

That is, after the choices are made, player II pays $K(x,y)$ to player I (so the game is zero-sum).

If the pair $(x,y)$ is interpreted as a point on the unit square, the figure shows the payoff to player I. Player I may adopt a mixed strategy, choosing a number according to a probability density function (pdf) $f$ , and similarly player II chooses from a pdf $g$ . Player I seeks to maximize the payoff $K(x,y)$ , player II to minimize the payoff, and each player is aware of the other's objective.

Game value

Sion and Wolfe show that

\sup _{f}\inf _{g}\iint K\,df\,dg={\frac {1}{3}}

but

\inf _{g}\sup _{f}\iint K\,df\,dg={\frac {3}{7}}.

These are the maximal and minimal expectations of the game's value of player I and II respectively.

The $\sup$ and $\inf$ respectively take the supremum and infimum over pdf's on the unit interval (actually Borel probability measures). These represent player I and player II's (mixed) strategies. Thus, player I can assure himself of a payoff of at least 3/7 if he knows player II's strategy, and player II can hold the payoff down to 1/3 if he knows player I's strategy.

There is no epsilon equilibrium for sufficiently small $\varepsilon$ , specifically, if $\varepsilon <{\frac {1}{2}}\left({\frac {3}{7}}-{\frac {1}{3}}\right)\simeq 0.0476$ . Dasgupta and Maskin^[2] assert that the game values are achieved if player I puts probability weight only on the set $\left\{0,1/2,1\right\}$ and player II puts weight only on $\left\{1/4,1/2,1\right\}$ .

Glicksberg's theorem shows that any zero-sum game with upper or lower semicontinuous payoff function has a value (in this context, an upper (lower) semicontinuous function K is one in which the set $\{P\mid K(P)<c\}$ (resp $\{P\mid K(P)>c\}$ ) is open for any real number c).

The payoff function of Sion and Wolfe's example is not semicontinuous. However, it may be made so by changing the value of K(x, x) and K(x, x + 1/2) (the payoff along the two discontinuities) to either +1 or −1, making the payoff upper or lower semicontinuous, respectively. If this is done, the game then has a value.

Generalizations

Subsequent work by Heuer^[3] discusses a class of games in which the unit square is divided into three regions, the payoff function being constant in each of the regions.

Related Research Articles

Minimax is a decision rule used in artificial intelligence, decision theory, game theory, statistics, and philosophy for minimizing the possible loss for a worst case scenario. When dealing with gains, it is referred to as "maximin" – to maximize the minimum gain. Originally formulated for several-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision-making in the presence of uncertainty.

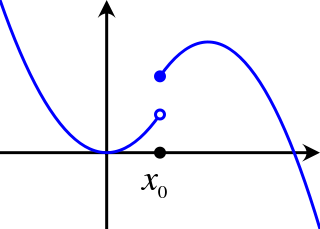
In mathematical analysis, semicontinuity is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function $is upper semicontinuous at a point if, roughly speaking, the function values for arguments near are not much higher than$

In game theory, a cooperative game is a game with competition between groups of players ("coalitions") due to the possibility of external enforcement of cooperative behavior. Those are opposed to non-cooperative games in which there is either no possibility to forge alliances or all agreements need to be self-enforcing.

In the branch of mathematics known as real analysis, the Darboux integral is constructed using Darboux sums and is one possible definition of the integral of a function. Darboux integrals are equivalent to Riemann integrals, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of the two integrals, if they exist, are equal. The definition of the Darboux integral has the advantage of being easier to apply in computations or proofs than that of the Riemann integral. Consequently, introductory textbooks on calculus and real analysis often develop Riemann integration using the Darboux integral, rather than the true Riemann integral. Moreover, the definition is readily extended to defining Riemann–Stieltjes integration. Darboux integrals are named after their inventor, Gaston Darboux (1842–1917).

In mathematics and mathematical optimization, the convex conjugate of a function is a generalization of the Legendre transformation which applies to non-convex functions. It is also known as Legendre–Fenchel transformation, Fenchel transformation, or Fenchel conjugate. It allows in particular for a far reaching generalization of Lagrangian duality.

Matching pennies is the name for a simple game used in game theory. It is played between two players, Even and Odd. Each player has a penny and must secretly turn the penny to heads or tails. The players then reveal their choices simultaneously. If the pennies match, then Even keeps both pennies, so wins one from Odd. If the pennies do not match Odd keeps both pennies, so receives one from Even.

The secretary problem demonstrates a scenario involving optimal stopping theory that is studied extensively in the fields of applied probability, statistics, and decision theory. It is also known as the marriage problem, the sultan's dowry problem, the fussy suitor problem, the googol game, and the best choice problem.

In game theory, folk theorems are a class of theorems describing an abundance of Nash equilibrium payoff profiles in repeated games. The original Folk Theorem concerned the payoffs of all the Nash equilibria of an infinitely repeated game. This result was called the Folk Theorem because it was widely known among game theorists in the 1950s, even though no one had published it. Friedman's (1971) Theorem concerns the payoffs of certain subgame-perfect Nash equilibria (SPE) of an infinitely repeated game, and so strengthens the original Folk Theorem by using a stronger equilibrium concept: subgame-perfect Nash equilibria rather than Nash equilibria.

In game theory, a repeated game is an extensive form game that consists of a number of repetitions of some base game. The stage game is usually one of the well-studied 2-person games. Repeated games capture the idea that a player will have to take into account the impact of his or her current action on the future actions of other players; this impact is sometimes called his or her reputation. Single stage game or single shot game are names for non-repeated games.

In mathematical optimization theory, duality or the duality principle is the principle that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem. If the primal is a minimization problem then the dual is a maximization problem. Any feasible solution to the primal (minimization) problem is at least as large as any feasible solution to the dual (maximization) problem. Therefore, the solution to the primal is an upper bound to the solution of the dual, and the solution of the dual is a lower bound to the solution of the primal. This fact is called weak duality.

In game theory, a stochastic game, introduced by Lloyd Shapley in the early 1950s, is a repeated game with probabilistic transitions played by one or more players. The game is played in a sequence of stages. At the beginning of each stage the game is in some state. The players select actions and each player receives a payoff that depends on the current state and the chosen actions. The game then moves to a new random state whose distribution depends on the previous state and the actions chosen by the players. The procedure is repeated at the new state and play continues for a finite or infinite number of stages. The total payoff to a player is often taken to be the discounted sum of the stage payoffs or the limit inferior of the averages of the stage payoffs.

In statistical decision theory, where we are faced with the problem of estimating a deterministic parameter (vector) $from observations an estimator is called minimax if its maximal risk is minimal among all estimators of . In a sense this means that is an estimator which performs best in the worst possible case allowed in the problem.$

In mathematics, and in particular game theory, Sion's minimax theorem is a generalization of John von Neumann's minimax theorem, named after Maurice Sion.

A continuous game is a mathematical concept, used in game theory, that generalizes the idea of an ordinary game like tic-tac-toe or checkers (draughts). In other words, it extends the notion of a discrete game, where the players choose from a finite set of pure strategies. The continuous game concepts allows games to include more general sets of pure strategies, which may be uncountably infinite.

In the study of zero sum games, Glicksberg's theorem is a result that shows certain games have a minimax value .

Congestion games are a class of games in game theory first proposed by American economist Robert W. Rosenthal in 1973. In a congestion game the payoff of each player depends on the resources it chooses and the number of players choosing the same resource. Congestion games are a special case of potential games. Rosenthal proved that any congestion game is a potential game and Monderer and Shapley (1996) proved the converse: for any potential game, there is a congestion game with the same potential function.

In algorithmic game theory, a succinct game or a succinctly representable game is a game which may be represented in a size much smaller than its normal form representation. Without placing constraints on player utilities, describing a game of $players, each facing strategies, requires listing utility values. Even trivial algorithms are capable of finding a Nash equilibrium in a time polynomial in the length of such a large input. A succinct game is of polynomial type if in a game represented by a string of length n the number of players, as well as the number of strategies of each player, is bounded by a polynomial in n .$

In decision theory and game theory, Wald's maximin model is a non-probabilistic decision-making model according to which decisions are ranked on the basis of their worst-case outcomes – the optimal decision is one with the least bad worst outcome. It is one of the most important models in robust decision making in general and robust optimization in particular.

In mathematics, the infinity Laplace operator is a 2nd-order partial differential operator, commonly abbreviated $. It is alternately defined by$

In probability theory and statistics, the Dirichlet process (DP) is one of the most popular Bayesian nonparametric models. It was introduced by Thomas Ferguson as a prior over probability distributions.

References

↑ Sion, Maurice; Wolfe, Phillip (1957), "On a game without a value", in Dresher, M.; Tucker, A. W.; Wolfe, P. (eds.), Contributions to the Theory of Games III, Annals of Mathematics Studies 39, Princeton University Press, pp. 299–306, ISBN 9780691079363
↑ P. Dasgupta and E. Maskin (1986). "The Existence of Equilibrium in Discontinuous Economic Games, I: Theory". Review of Economic Studies . 53 (1): 1–26. doi:10.2307/2297588. JSTOR 2297588.
↑ G. A. Heuer (2001). "Three-part partition games on rectangles". Theoretical Computer Science. 259: 639–661. doi: 10.1016/S0304-3975(00)00404-7 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Sion, Maurice; Wolfe, Phillip (1957), "On a game without a value", in Dresher, M.; Tucker, A. W.; Wolfe, P. (eds.), Contributions to the Theory of Games III, Annals of Mathematics Studies 39, Princeton University Press, pp. 299–306, ISBN 9780691079363

[2] P. Dasgupta and E. Maskin (1986). "The Existence of Equilibrium in Discontinuous Economic Games, I: Theory". Review of Economic Studies . 53 (1): 1–26. doi:10.2307/2297588. JSTOR 2297588.

[3] G. A. Heuer (2001). "Three-part partition games on rectangles". Theoretical Computer Science. 259: 639–661. doi: 10.1016/S0304-3975(00)00404-7 .

[1]

[2]

[3]