Differential geometry is a mathematical discipline that uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra to study problems in geometry. The theory of plane and space curves and surfaces in the three-dimensional Euclidean space formed the basis for development of differential geometry during the 18th century and the 19th century.

In mathematics, a Lie group is a group that is also a differentiable manifold, with the property that the group operations are smooth. Lie groups are named after Norwegian mathematician Sophus Lie, who laid the foundations of the theory of continuous transformation groups.
Noncommutative geometry (NCG) is a branch of mathematics concerned with a geometric approach to noncommutative algebras, and with the construction of spaces that are locally presented by noncommutative algebras of functions. A noncommutative algebra is an associative algebra in which the multiplication is not commutative, that is, for which does not always equal ; or more generally an algebraic structure in which one of the principal binary operations is not commutative; one also allows additional structures, e.g. topology or norm, to be possibly carried by the noncommutative algebra of functions.
In mathematics, two linear operators are called isospectral or cospectral if they have the same spectrum. Roughly speaking, they are supposed to have the same sets of eigenvalues, when those are counted with multiplicity.
In mathematics and especially differential geometry, a Kähler manifold is a manifold with three mutually compatible structures: a complex structure, a Riemannian structure, and a symplectic structure. The concept was first studied by Jan Arnoldus Schouten and David van Dantzig in 1930, and then introduced by Erich Kähler in 1933. The terminology has been fixed by André Weil.
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic.
In mathematics, spectral graph theory is the study of the properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated with the graph, such as its adjacency matrix or Laplacian matrix.

In mathematics, an arithmetic group is a group obtained as the integer points of an algebraic group, for example They arise naturally in the study of arithmetic properties of quadratic forms and other classical topics in number theory. They also give rise to very interesting examples of Riemannian manifolds and hence are objects of interest in differential geometry and topology. Finally, these two topics join in the theory of automorphic forms which is fundamental in modern number theory.
Hopf–Rinow theorem is a set of statements about the geodesic completeness of Riemannian manifolds. It is named after Heinz Hopf and his student Willi Rinow, who published it in 1931.
In mathematics, the Selberg trace formula, introduced by Selberg (1956), is an expression for the character of the unitary representation of G on the space L2(G/Γ) of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group. The character is given by the trace of certain functions on G.

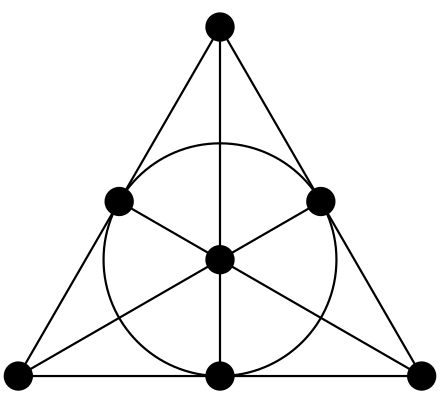
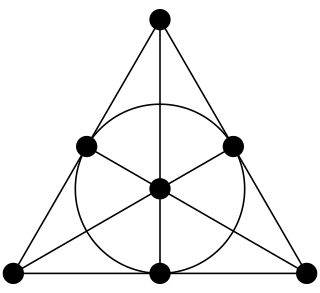
To hear the shape of a drum is to infer information about the shape of the drumhead from the sound it makes, i.e., from the list of overtones, via the use of mathematical theory. "Can One Hear the Shape of a Drum?" was the title of an article by Mark Kac in the American Mathematical Monthly in 1966, but the phrasing of the title is due to Lipman Bers. These questions can be traced back all the way to Hermann Weyl.

In mathematics, a Kleinian group is a discrete subgroup of PSL(2, C). The group PSL(2, C) of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic space H3, and as orientation preserving conformal maps of the open unit ball B3 in R3 to itself. Therefore, a Kleinian group can be regarded as a discrete subgroup acting on one of these spaces.
The Selberg zeta-function was introduced by Atle Selberg (1956). It is analogous to the famous Riemann zeta function
In mathematics, the Abel–Jacobi map is a construction of algebraic geometry which relates an algebraic curve to its Jacobian variety. In Riemannian geometry, it is a more general construction mapping a manifold to its Jacobi torus. The name derives from the theorem of Abel and Jacobi that two effective divisors are linearly equivalent if and only if they are indistinguishable under the Abel–Jacobi map.
Arthur Besse is a pseudonym chosen by a group of French differential geometers, led by Marcel Berger, following the model of Nicolas Bourbaki. A number of monographs have appeared under the name.
Spectral geometry is a field in mathematics which concerns relationships between geometric structures of manifolds and spectra of canonically defined differential operators. The case of the Laplace–Beltrami operator on a closed Riemannian manifold has been most intensively studied, although other Laplace operators in differential geometry have also been examined. The field concerns itself with two kinds of questions: direct problems and inverse problems.

Toshikazu Sunada is a Japanese mathematician and author of many books and essays on mathematics and mathematical sciences. He is professor of mathematics at Meiji University, Tokyo, and is also professor emeritus of Tohoku University, Tohoku, Japan. Before he joined Meiji University in 2003, he was professor of mathematics at Nagoya University (1988–1991), at the University of Tokyo (1991–1993), and at Tohoku University (1993–2003). Sunada was involved in the creation of the School of Interdisciplinary Mathematical Sciences at Meiji University and is its first dean (2013–2017).
Carolyn S. Gordon is a mathematician and Benjamin Cheney Professor of Mathematics at Dartmouth College. She is most well known for giving a negative answer to the question "Can you hear the shape of a drum?" in her work with David Webb and Scott A. Wolpert. She is a Chauvenet Prize winner and a 2010 Noether Lecturer.
Fritz Gassmann (1899–1990) was a Swiss mathematician and geophysicist.
Gassmann or Gaßmann is a German surname. Notable people with the surname include: