Gempack

Last updated

GEMPACK (General Equilibrium Modelling PACKage) is a modeling system for CGE economic models, used at the Centre of Policy Studies (CoPS) in Melbourne, Australia, and sold to other CGE modellers.

Contents

Some of the more well-known CGE models solved using GEMPACK [1] are the GTAP model of world trade, and the MONASH, MMRF, ORANI-G and TERM models used at CoPS. All these models share a distinctive feature: they are formulated as a system of differential equations in percentage change form; however, this is not required by GEMPACK.

Main features

A characteristic feature of CGE models is that an initial solution for the model can be readily constructed from a table of transaction values (such as an input-output table or a social accounting matrix) that satisfies certain basic accounting restrictions. GEMPACK builds on this feature by formulating the CGE model as an initial value problem which is solved using standard techniques.

The GEMPACK user specifies her model by constructing a text file listing model equations and variables, and showing how variables relate to value flows stored on an initial data file.

GEMPACK translates this file into a computer program which solves the model, i.e., computes how model variables might change in response to an external shock. The original equation system is linearized (reformulated as a system of first-order partial differential equations). If most variables are expressed in terms of percentage changes (akin to log changes) the coefficients of the linearized system are usually very simple functions of database value flows.

Computer algebra is used at this point to greatly reduce (by substitution) the size of the system. Then it is solved by multistep methods such as the Euler method, midpoint method or Gragg's modified Midpoint method. These all require solution of a large system of linear equations; accomplished by sparse matrix techniques. Richardson extrapolation is used to improve accuracy. The final result is an accurate solution of the original non-linear equations.

This linearized approach, originally devised to solve medium-sized CGE models on early computers, has since proved capable (on modern computers) of solving very large models. Additionally it has lent itself to some interesting extensions, such as: a Gaussian quadrature method [2] of estimating confidence intervals for model results from known distributions of shock or parameter values; a way to formulate inequality constraints or non-differentiable equations as complementarities; [3] and a technique [4] to decompose changes in model variables due to several shocks into components due to each individual shock.

The underlying numerical approach is complemented by several GUI programs that: ease viewing of large multidimensional arrays often found in CGE databases; manage complex (e.g., multi-period) simulations; and allow interactive exploration and explanation of simulation results.

See also

Related Research Articles

<span class="mw-page-title-main">Numerical analysis</span> Study of algorithms using numerical approximation

Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis. It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics, numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine and biology.

In economics, general equilibrium theory attempts to explain the behavior of supply, demand, and prices in a whole economy with several or many interacting markets, by seeking to prove that the interaction of demand and supply will result in an overall general equilibrium. General equilibrium theory contrasts to the theory of partial equilibrium, which analyzes a specific part of an economy while its other factors are held constant. In general equilibrium, constant influences are considered to be noneconomic, therefore, resulting beyond the natural scope of economic analysis. The noneconomic influences is possible to be non-constant when the economic variables change, and the prediction accuracy may depend on the independence of the economic factors.

<span class="mw-page-title-main">Mathematical optimization</span> Study of mathematical algorithms for optimization problems

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.

<span class="mw-page-title-main">Computational physics</span> Numerical simulations of physical problems via computers

Computational physics is the study and implementation of numerical analysis to solve problems in physics. Historically, computational physics was the first application of modern computers in science, and is now a subset of computational science. It is sometimes regarded as a subdiscipline of theoretical physics, but others consider it an intermediate branch between theoretical and experimental physics - an area of study which supplements both theory and experiment.

<span class="mw-page-title-main">System of linear equations</span> Several equations of degree 1 to be solved simultaneously

In mathematics, a system of linear equations is a collection of one or more linear equations involving the same variables.

<span class="mw-page-title-main">Computational fluid dynamics</span> Analysis and solving of problems that involve fluid flows

Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests.

A hybrid system is a dynamical system that exhibits both continuous and discrete dynamic behavior – a system that can both flow and jump. Often, the term "hybrid dynamical system" is used, to distinguish over hybrid systems such as those that combine neural nets and fuzzy logic, or electrical and mechanical drivelines. A hybrid system has the benefit of encompassing a larger class of systems within its structure, allowing for more flexibility in modeling dynamic phenomena.

Computational science, also known as scientific computing, technical computing or scientific computation (SC), is an area of science that uses advanced computing capabilities to understand and solve complex physical problems. This includes

The general algebraic modeling system (GAMS) is a high-level modeling system for mathematical optimization. GAMS is designed for modeling and solving linear, nonlinear, and mixed-integer optimization problems. The system is tailored for complex, large-scale modeling applications and allows the user to build large maintainable models that can be adapted to new situations. The system is available for use on various computer platforms. Models are portable from one platform to another.

Numerical methods for partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations (PDEs).

Computable general equilibrium (CGE) models are a class of economic models that use actual economic data to estimate how an economy might react to changes in policy, technology or other external factors. CGE models are also referred to as AGE models.

In mathematical economics, applied general equilibrium (AGE) models were pioneered by Herbert Scarf at Yale University in 1967, in two papers, and a follow-up book with Terje Hansen in 1973, with the aim of empirically estimating the Arrow–Debreu model of general equilibrium theory with empirical data, to provide "“a general method for the explicit numerical solution of the neoclassical model” (Scarf with Hansen 1973: 1)

Numerical linear algebra, sometimes called applied linear algebra, is the study of how matrix operations can be used to create computer algorithms which efficiently and accurately provide approximate answers to questions in continuous mathematics. It is a subfield of numerical analysis, and a type of linear algebra. Computers use floating-point arithmetic and cannot exactly represent irrational data, so when a computer algorithm is applied to a matrix of data, it can sometimes increase the difference between a number stored in the computer and the true number that it is an approximation of. Numerical linear algebra uses properties of vectors and matrices to develop computer algorithms that minimize the error introduced by the computer, and is also concerned with ensuring that the algorithm is as efficient as possible.

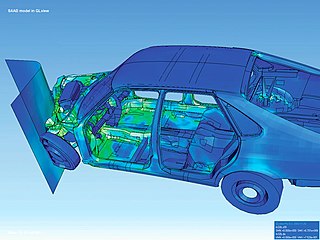
<span class="mw-page-title-main">Finite element method</span> Numerical method for solving physical or engineering problems

The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential.

Combustion models for CFD refers to combustion models for computational fluid dynamics. Combustion is defined as a chemical reaction in which a hydrocarbon fuel reacts with an oxidant to form products, accompanied with the release of energy in the form of heat. Being the integral part of various engineering applications like: internal combustion engines, aircraft engines, rocket engines, furnaces, and power station combustors, combustion manifests itself as a wide domain during the design, analysis and performance characteristics stages of the above-mentioned applications. With the added complexity of chemical kinetics and achieving reacting flow mixture environment, proper modeling physics has to be incorporated during computational fluid dynamic (CFD) simulations of combustion. Hence the following discussion presents a general outline of the various adequate models incorporated with the Computational fluid dynamic code to model the process of combustion.

PROSE was the mathematical 4GL virtual machine that established the holistic modeling paradigm known as Synthetic Calculus. A successor to the SLANG/CUE simulation and optimization language developed at TRW Systems, it was introduced in 1974 on Control Data supercomputers. It was the first commercial language to employ automatic differentiation (AD), which was optimized to loop in the instruction-stack of the CDC 6600 CPU.

Algebraic modeling languages like AIMMS, AMPL, GAMS, MPL and others have been developed to facilitate the description of a problem in mathematical terms and to link the abstract formulation with data-management systems on the one hand and appropriate algorithms for solution on the other. Robust algorithms and modeling language interfaces have been developed for a large variety of mathematical programming problems such as linear programs (LPs), nonlinear programs (NPs), Mixed Integer Programs (MIPs), mixed complementarity programs (MCPs) and others. Researchers are constantly updating the types of problems and algorithms that they wish to use to model in specific domain applications.

Validated numerics, or rigorous computation, verified computation, reliable computation, numerical verification is numerics including mathematically strict error evaluation, and it is one field of numerical analysis. For computation, interval arithmetic is used, and all results are represented by intervals. Validated numerics were used by Warwick Tucker in order to solve the 14th of Smale's problems, and today it is recognized as a powerful tool for the study of dynamical systems.

Probabilistic numerics is a scientific field at the intersection of statistics, machine learning and applied mathematics, where tasks in numerical analysis including finding numerical solutions for integration, linear algebra, optimisation and differential equations are seen as problems of statistical, probabilistic, or Bayesian inference.

References

  1. ↑ Harrison, W. J. and K. R. Pearson (1996), "Computing Solutions for Large General Equilibrium Models Using GEMPACK", Computational Economics, vol. 9, pp. 83–127.
  2. ↑ DeVuyst, E. A. and P. V. Preckel (1997), "Sensitivity Analysis Revisited: A Quadrature-Based Approach", Journal of Policy Modeling , 19(2) pp. 175–185.
  3. ↑ Harrison, W. J., J. M. Horridge, K. R. Pearson and G. Wittwer (2004), "A Practical Method for Explicitly Modeling Quotas and Other Complementarities", Computational Economics, June 2004, Vol. 23(4), pp. 325–341.
  4. ↑ Harrison, W. J., J. M. Horridge and K. R. Pearson (2000), "Decomposing Simulation Results with respect to Exogenous Shocks", Computational Economics, Vol 15(3), pp. 227–249.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.