In physics, the cross section is a measure of the probability that a specific process will take place when some kind of radiant excitation intersects a localized phenomenon. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during a collision with an atomic nucleus. Cross section is typically denoted σ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

A normal distribution is a probability distribution used to model phenomena that have a default behaviour and cumulative possible deviations from that behaviour. For instance, a proficient archer's arrows are expected to land around the bull's eye of the target; however, due to aggregating imperfections in the archer's technique, most arrows will miss the bull's eye by some distance. The average of this distance is known in archery as accuracy, while the amount of variation in the distances as precision. In the context of a normal distribution, accuracy and precision are referred to as the mean and the standard deviation, respectively. Thus, a narrow measure of an archer's proficiency can be expressed with two values: a mean and a standard deviation. In a normal distribution, these two values mean: there is a ~68% probability that an arrow will land within one standard deviation of the archer's average accuracy; a ~95% probability that an arrow will land within two standard deviations of the archer's average accuracy; ~99.7% within three; and so on, slowly increasing towards 100%.

The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor physical quantity that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields. This density and flux of energy and momentum are the sources of the gravitational field in the Einstein field equations of general relativity, just as mass density is the source of such a field in Newtonian gravity.

In nuclear engineering, a critical mass is the smallest amount of fissile material needed for a sustained nuclear chain reaction. The critical mass of a fissionable material depends upon its nuclear properties, density, shape, enrichment, purity, temperature, and surroundings. The concept is important in nuclear weapon design.

Neutron transport is the study of the motions and interactions of neutrons with materials. Nuclear scientists and engineers often need to know where neutrons are in an apparatus, what direction they are going, and how quickly they are moving. It is commonly used to determine the behavior of nuclear reactor cores and experimental or industrial neutron beams. Neutron transport is a type of radiative transport.

In nuclear and particle physics, the concept of a neutron cross section is used to express the likelihood of interaction between an incident neutron and a target nucleus. In conjunction with the neutron flux, it enables the calculation of the reaction rate, for example to derive the thermal power of a nuclear power plant. The standard unit for measuring the cross section is the barn, which is equal to 10−28 m2 or 10−24 cm2. The larger the neutron cross section, the more likely a neutron will react with the nucleus.
In general relativity, a frame field is a set of four pointwise-orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime. The timelike unit vector field is often denoted by and the three spacelike unit vector fields by . All tensorial quantities defined on the manifold can be expressed using the frame field and its dual coframe field.
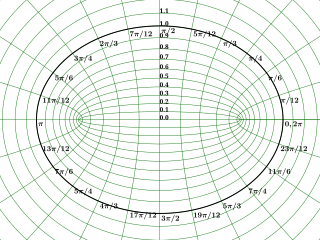
In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal ellipses and hyperbolae. The two foci and are generally taken to be fixed at and , respectively, on the -axis of the Cartesian coordinate system.
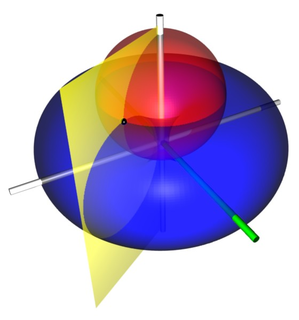
Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci and in bipolar coordinates become a ring of radius in the plane of the toroidal coordinate system; the -axis is the axis of rotation. The focal ring is also known as the reference circle.

Elliptic cylindrical coordinates are a three-dimensional orthogonal coordinate system that results from projecting the two-dimensional elliptic coordinate system in the perpendicular -direction. Hence, the coordinate surfaces are prisms of confocal ellipses and hyperbolae. The two foci and are generally taken to be fixed at and , respectively, on the -axis of the Cartesian coordinate system.

Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the focal axis of the ellipse, i.e., the symmetry axis on which the foci are located. Rotation about the other axis produces oblate spheroidal coordinates. Prolate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two smallest principal axes are equal in length.

Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of radius in the x-y plane. Oblate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two largest semi-axes are equal in length.
In mathematics, the theory of optimal stopping or early stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance. A key example of an optimal stopping problem is the secretary problem. Optimal stopping problems can often be written in the form of a Bellman equation, and are therefore often solved using dynamic programming.
The four-factor formula, also known as Fermi's four factor formula is used in nuclear engineering to determine the multiplication of a nuclear chain reaction in an infinite medium.
In quantum field theory, a non-topological soliton (NTS) is a soliton field configuration possessing, contrary to a topological one, a conserved Noether charge and stable against transformation into usual particles of this field for the following reason. For fixed charge Q, the mass sum of Q free particles exceeds the energy (mass) of the NTS so that the latter is energetically favorable to exist.
The six-factor formula is used in nuclear engineering to determine the multiplication of a nuclear chain reaction in a non-infinite medium.

Bending of plates, or plate bending, refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the plate can be calculated from these deflections. Once the stresses are known, failure theories can be used to determine whether a plate will fail under a given load.
Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used to analyze the motion of a system of discrete particles each with a finite number of degrees of freedom. Lagrangian field theory applies to continua and fields, which have an infinite number of degrees of freedom.
Menter's Shear Stress Transport turbulence model, or SST, is a widely used and robust two-equation eddy-viscosity turbulence model used in Computational Fluid Dynamics. The model combines the k-omega turbulence model and K-epsilon turbulence model such that the k-omega is used in the inner region of the boundary layer and switches to the k-epsilon in the free shear flow.
The pressuron is a hypothetical scalar particle which couples to both gravity and matter theorised in 2013. Although originally postulated without self-interaction potential, the pressuron is also a dark energy candidate when it has such a potential. The pressuron takes its name from the fact that it decouples from matter in pressure-less regimes, allowing the scalar-tensor theory of gravity involving it to pass solar system tests, as well as tests on the equivalence principle, even though it is fundamentally coupled to matter. Such a decoupling mechanism could explain why gravitation seems to be well described by general relativity at present epoch, while it could actually be more complex than that. Because of the way it couples to matter, the pressuron is a special case of the hypothetical string dilaton. Therefore, it is one of the possible solutions to the present non-observation of various signals coming from massless or light scalar fields that are generically predicted in string theory.




























