
David Hilbert was a German mathematician and one of the most influential mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas including invariant theory, the calculus of variations, commutative algebra, algebraic number theory, the foundations of geometry, spectral theory of operators and its application to integral equations, mathematical physics, and the foundations of mathematics.
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points to Euclidean points, and vice versa.
Synthetic geometry is geometry without the use of coordinates. It relies on the axiomatic method for proving all results from a few basic properties initially called postulate, and at present called axioms.

In projective geometry, Desargues's theorem, named after Girard Desargues, states:

In mathematics, a saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero, but which is not a local extremum of the function. An example of a saddle point is when there is a critical point with a relative minimum along one axial direction and at a relative maximum along the crossing axis. However, a saddle point need not be in this form. For example, the function has a critical point at that is a saddle point since it is neither a relative maximum nor relative minimum, but it does not have a relative maximum or relative minimum in the -direction.
In the differential geometry of surfaces, an asymptotic curve is a curve always tangent to an asymptotic direction of the surface. It is sometimes called an asymptotic line, although it need not be a line.
In mathematics, incidence geometry is the study of incidence structures. A geometric structure such as the Euclidean plane is a complicated object that involves concepts such as length, angles, continuity, betweenness, and incidence. An incidence structure is what is obtained when all other concepts are removed and all that remains is the data about which points lie on which lines. Even with this severe limitation, theorems can be proved and interesting facts emerge concerning this structure. Such fundamental results remain valid when additional concepts are added to form a richer geometry. It sometimes happens that authors blur the distinction between a study and the objects of that study, so it is not surprising to find that some authors refer to incidence structures as incidence geometries.

Stefan Cohn-Vossen was a mathematician, who was responsible for Cohn-Vossen's inequality and the Cohn-Vossen transformation is also named after him. He proved the first version of the splitting theorem.

In geometry, the center of curvature of a curve is found at a point that is at a distance from the curve equal to the radius of curvature lying on the normal vector. It is the point at infinity if the curvature is zero. The osculating circle to the curve is centered at the centre of curvature. Cauchy defined the center of curvature C as the intersection point of two infinitely close normal lines to the curve. The locus of centers of curvature for each point on the curve comprise the evolute of the curve. This term is generally used in physics regarding the study of lenses and mirrors.

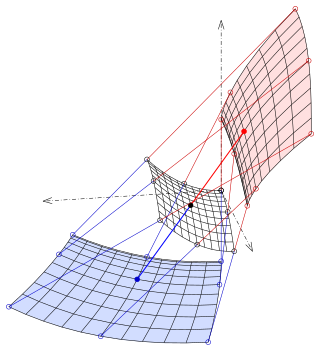
In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.

In geometry, the Desargues configuration is a configuration of ten points and ten lines, with three points per line and three lines per point. It is named after Girard Desargues.
For a surface in three dimension the focal surface, surface of centers or evolute is formed by taking the centers of the curvature spheres, which are the tangential spheres whose radii are the reciprocals of one of the principal curvatures at the point of tangency. Equivalently it is the surface formed by the centers of the circles which osculate the curvature lines.

In the mathematical study of the differential geometry of surfaces, a tangent developable is a particular kind of developable surface obtained from a curve in Euclidean space as the surface swept out by the tangent lines to the curve. Such a surface is also the envelope of the tangent planes to the curve.

In geometry, a surface of constant width is a convex form whose width, measured by the distance between two opposite parallel planes touching its boundary, is the same regardless of the direction of those two parallel planes. One defines the width of the surface in a given direction to be the perpendicular distance between the parallels perpendicular to that direction. Thus, a surface of constant width is the three-dimensional analogue of a curve of constant width, a two-dimensional shape with a constant distance between pairs of parallel tangent lines.
In differential geometry, the Carathéodory conjecture is a mathematical conjecture attributed to Constantin Carathéodory by Hans Ludwig Hamburger in a session of the Berlin Mathematical Society in 1924. Carathéodory did publish a paper on a related subject, but never committed the conjecture into writing. In, John Edensor Littlewood mentions the conjecture and Hamburger's contribution as an example of a mathematical claim that is easy to state but difficult to prove. Dirk Struik describes in the formal analogy of the conjecture with the Four Vertex Theorem for plane curves. Modern references to the conjecture are the problem list of Shing-Tung Yau, the books of Marcel Berger, as well as the books.
Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.

In geometry, the Reye configuration, introduced by Theodor Reye (1882), is a configuration of 12 points and 16 lines. Each point of the configuration belongs to four lines, and each line contains three points. Therefore, in the notation of configurations, the Reye configuration is written as 124163.
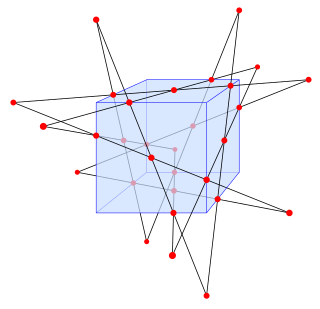
In geometry, the Schläfli double six is a configuration of 30 points and 12 lines in three-dimensional Euclidean space, introduced by Ludwig Schläfli in 1858. The lines of the configuration can be partitioned into two subsets of six lines: each line is disjoint from (skew with) the lines in its own subset of six lines, and intersects all but one of the lines in the other subset of six lines. Each of the 12 lines of the configuration contains five intersection points, and each of these 30 intersection points belongs to exactly two lines, one from each subset, so in the notation of configurations the Schläfli double six is written 302125.
In mathematics, a geometric transformation is any bijection of a set to itself with some salient geometrical underpinning. More specifically, it is a function whose domain and range are sets of points — most often both or both — such that the function is bijective so that its inverse exists. The study of geometry may be approached by the study of these transformations.
John Michael Pickering was a twentieth-century British sculptor who pioneered the use of mathematics in British art.











