This is a glossary of graph theory terms. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by edges.

In mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics.

In the area of modern algebra known as group theory, the Higman–Sims group HS is a sporadic simple group of order

In the mathematical discipline of graph theory, a wheel graph is a graph formed by connecting a single universal vertex to all vertices of a cycle. A wheel graph with n vertices can also be defined as the 1-skeleton of an (n-1)-gonal pyramid. Some authors write Wn to denote a wheel graph with n vertices ; other authors instead use Wn to denote a wheel graph with n+1 vertices, which is formed by connecting a single vertex to all vertices of a cycle of length n. In the rest of this article we use the former notation.

In the mathematical field of graph theory, the Hoffman–Singleton graph is a 7-regular undirected graph with 50 vertices and 175 edges. It is the unique strongly regular graph with parameters (50,7,0,1). It was constructed by Alan Hoffman and Robert Singleton while trying to classify all Moore graphs, and is the highest order Moore graph known to exist. Since it is a Moore graph where each vertex has degree 7, and the girth is 5, it is a (7,5)-cage.
Some of the finite structures considered in graph theory have names, sometimes inspired by the graph's topology, and sometimes after their discoverer. A famous example is the Petersen graph, a concrete graph on 10 vertices that appears as a minimal example or counterexample in many different contexts.

In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed by choosing independently at random for each pair of its vertices whether to connect the vertices by an edge. The names of this graph honor Richard Rado, Paul Erdős, and Alfréd Rényi, mathematicians who studied it in the early 1960s; it appears even earlier in the work of Wilhelm Ackermann (1937). The Rado graph can also be constructed non-randomly, by symmetrizing the membership relation of the hereditarily finite sets, by applying the BIT predicate to the binary representations of the natural numbers, or as an infinite Paley graph that has edges connecting pairs of prime numbers congruent to 1 mod 4 that are quadratic residues modulo each other.

In graph theory, a branch of mathematics, an undirected graph is called an asymmetric graph if it has no nontrivial symmetries.
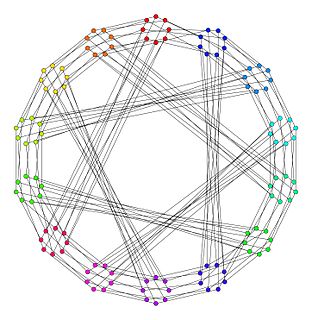
In the mathematical field of graph theory, the Ljubljana graph is an undirected bipartite graph with 112 vertices and 168 edges.
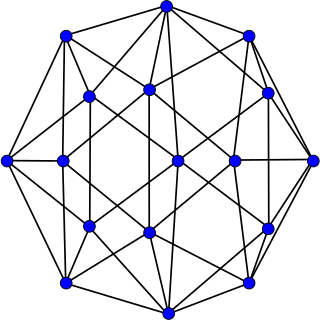
In the mathematical field of graph theory, the Errera graph is a graph with 17 vertices and 45 edges. Alfred Errera published it in 1921 as a counterexample to Kempe's erroneous proof of the four color theorem; it was named after Errera by Hutchinson & Wagon (1998).
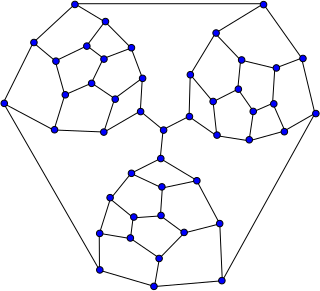
In the mathematical field of graph theory, the Tutte graph is a 3-regular graph with 46 vertices and 69 edges named after W. T. Tutte. It has chromatic number 3, chromatic index 3, girth 4 and diameter 8.

In graph theory and statistics, a graphon is a symmetric measurable function , that is important in the study of dense graphs. Graphons arise as the fundamental objects in two areas: as the defining objects of exchangeable random graph models and as a natural notion of limit for sequences of dense graphs. Graphons are tied to dense graphs by the following pair of observations: the random graph models defined by graphons give rise to dense graphs almost surely, and, by the regularity lemma, graphons capture the structure of arbitrary large dense graphs.

In the mathematical field of graph theory, the Klein graphs are two different but related regular graphs, each with 84 edges. Each can be embedded in the orientable surface of genus 3, in which they form dual graphs.
In graph theory, a quotient graphQ of a graph G is a graph whose vertices are blocks of a partition of the vertices of G and where block B is adjacent to block C if some vertex in B is adjacent to some vertex in C with respect to the edge set of G. In other words, if G has edge set E and vertex set V and R is the equivalence relation induced by the partition, then the quotient graph has vertex set V/R and edge set {([u]R, [v]R) | (u, v) ∈ E(G)}.
An eodermdrome is a form of word play wherein a word is formed from a set of letters in such a way that it has a non-planar spelling net. Gary S. Bloom, Allan Gewirtz, John W. Kennedy, and Peter J. Wexler first described the eodermdrome in May 1980, and it subsequently became more widely known after publication in Word Ways: The Journal of Recreational Linguistics in August 1980.

In graph theory, a Ptolemaic graph is an undirected graph whose shortest path distances obey Ptolemy's inequality, which in turn was named after the Greek astronomer and mathematician Ptolemy. The Ptolemaic graphs are exactly the graphs that are both chordal and distance-hereditary; they include the block graphs and are a subclass of the perfect graphs.

The M22 graph, also called the Mesner graph, is the unique strongly regular graph with parameters (77, 16, 0, 4). It is constructed from the Steiner system (3, 6, 22) by representing its 77 blocks as vertices and joining two vertices iff they have no terms in common or by deleting a vertex and its neighbors from the Higman–Sims graph.
In graph theory, the Games graph is the largest known locally linear strongly regular graph. Its parameters as a strongly regular graph are (729,112,1,20). This means that it has 729 vertices, and 40824 edges. Each edge is in a unique triangle and each non-adjacent pair of vertices have exactly 20 shared neighbors. It is named after Richard A. Games, who suggested its construction in an unpublished communication and wrote about related constructions.