Gilbreath shuffle

Last updated August 17, 2023

A Gilbreath shuffle is a way to shuffle a deck of cards, named after mathematician Norman Gilbreath (also known for Gilbreath's conjecture). Gilbreath's principle describes the properties of a deck that are preserved by this type of shuffle, and a Gilbreath permutation is a permutation that can be formed by a Gilbreath shuffle.^[1]

Description

A Gilbreath shuffle consists of the following two steps:^[1]

Deal off any number of the cards from the top of a deck to form a second pile of cards.
Riffle the new pile with the remainder of the deck.

It differs from the more commonly used procedure of cutting a deck into two piles and then riffling the piles, in that the first step of dealing off cards reverses the order of the cards in the new pile, whereas cutting the deck would preserve this order.

Gilbreath's principle

Although seemingly highly random, Gilbreath shuffles preserve many properties of the initial deck. For instance, if the initial deck of cards alternates between black and red cards, then after a single Gilbreath shuffle the deck will still have the property that, if it is grouped into consecutive pairs of cards, each pair will have one black card and one red card. Similarly, if a Gilbreath shuffle is used on a deck of cards where every card has the same suit as the card four positions prior, and the resulting deck is grouped into consecutive sets of four cards, then each set will contain one card of each suit. This phenomenon is known as Gilbreath's principle and is the basis for several card tricks.^[1]

Gilbreath permutations

Mathematically, Gilbreath shuffles can be described by Gilbreath permutations, permutations of the numbers from 1 to n that can be obtained by a Gilbreath shuffle with a deck of cards labeled with these numbers in order. Gilbreath permutations can be characterized by the property that every prefix contains a consecutive set of numbers.^[1] For instance, the permutation (5,6,4,7,8,3,2,9,1,10) is a Gilbreath permutation for n = 10 that can be obtained by dealing off the first four or five cards and riffling them with the rest. Each of its prefixes (5), (5,6), (5,6,4), (5,6,4,7), etc. contain a set of numbers that (when sorted) form a consecutive subsequence of the numbers from 1 to 10. Equivalently, in terms of permutation patterns, the Gilbreath permutations are the permutations that avoid the two patterns 132 and 312.^[2]

A Gilbreath shuffle may be uniquely determined by specifying which of the positions in the resulting shuffled deck are occupied by cards that were dealt off into the second pile, and which positions are occupied by cards that were not dealt off. Therefore, there are $2^{n}$ possible ways of performing a Gilbreath shuffle on a deck of $n$ cards. However, each Gilbreath permutation may be obtained from two different Gilbreath shuffles, as the first position of the permutation may have come from either of the two piles. Therefore, there are $2^{n-1}$ distinct Gilbreath permutations.^[1]^[3]

The cyclic Gilbreath permutations of order $n$ are in one-to-one correspondence with the real numbers $c$ for which the iteration $x\mapsto x^{2}+c$ (starting from $x=0$ ) underlying the Mandelbrot set is periodic with period $n$ . In this correspondence, the permutation that corresponds to a given value $c$ describes the numerical sorted order of the iterates for $c$ .^[1] The number of cyclic Gilbreath permutations (and therefore also the number of real periodic points of the Mandelbrot set), for $n=1,2,3,\dots$ , is given by the integer sequence

1, 1, 1, 2, 3, 5, 9, 16, 28, 51, 93, 170, 315, 585, 1091, ... (sequence A000048 in the OEIS).

Ultimate Gilbreath principle

{\begin{matrix}1\\2\\3\\4\\5\\6\\7\\8\\9\\10\end{matrix}}\to {\begin{matrix}5\\6\\7\\8\\9\\10\end{matrix}}{\begin{matrix}4\\3\\2\\1\end{matrix}}\to {\begin{matrix}4\\5\\6\\3\\7\\2\\8\\9\\1\\10\end{matrix}}

Here is an example illustrating the theorem. For a ten-card deck, we can deal off four cards into a small pile on the table (one by one) and then riffle shuffle them to lead to the arrangement π above

A theorem called "the ultimate Gilbreath principle" states that, for a permutation $\pi$ of $\{1,2,3,\dots ,n\}$ , the following four properties are equivalent:^[1]

$\pi$ is a Gilbreath permutation.
For each $j$ , the top $j$ cards $\pi (1),\dots \pi (j)$ are distinct modulo $j$ .
For each $j$ and $k$ with $kj\leq n$ , the $j$ cards $\pi {\bigl (}(k-1)j+1{\bigr )},\pi {\bigl (}k-1)j+2{\bigr )},\dots ,\pi (kj)$ are distinct modulo $j$ .
For each $j$ , the top $j$ cards are consecutive in $1,2,\dots ,n$ .

Related Research Articles

Shuffling is a procedure used to randomize a deck of playing cards to provide an element of chance in card games. Shuffling is often followed by a cut, to help ensure that the shuffler has not manipulated the outcome.

<span class="mw-page-title-main">Simplex</span> Multi-dimensional generalization of triangle

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example,

In mathematics, a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements. The word "permutation" also refers to the act or process of changing the linear order of an ordered set.

In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.

In mathematics, a stochastic matrix is a square matrix used to describe the transitions of a Markov chain. Each of its entries is a nonnegative real number representing a probability. It is also called a probability matrix, transition matrix, substitution matrix, or Markov matrix. The stochastic matrix was first developed by Andrey Markov at the beginning of the 20th century, and has found use throughout a wide variety of scientific fields, including probability theory, statistics, mathematical finance and linear algebra, as well as computer science and population genetics. There are several different definitions and types of stochastic matrices:

In mathematics, particularly in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry of 1 in each row and each column and 0s elsewhere. Each such matrix, say $P$ , represents a permutation of $m$ elements and, when used to multiply another matrix, say $A$ , results in permuting the rows or columns of the matrix $A$ .

In combinatorics, a branch of mathematics, the inclusion–exclusion principle is a counting technique which generalizes the familiar method of obtaining the number of elements in the union of two finite sets; symbolically expressed as

In mathematics, the double factorial of a number $n$ , denoted by $n ‼$ , is the product of all the positive integers up to $n$ that have the same parity as $n$ . That is,

In mathematics, especially in combinatorics, Stirling numbers of the first kind arise in the study of permutations. In particular, the Stirling numbers of the first kind count permutations according to their number of cycles.

The Steinhaus–Johnson–Trotter algorithm or Johnson–Trotter algorithm, also called plain changes, is an algorithm named after Hugo Steinhaus, Selmer M. Johnson and Hale F. Trotter that generates all of the permutations of $elements. Each permutation in the sequence that it generates differs from the previous permutation by swapping two adjacent elements of the sequence. Equivalently, this algorithm finds a Hamiltonian cycle in the permutohedron.$

In mathematics, especially in linear algebra and matrix theory, the commutation matrix is used for transforming the vectorized form of a matrix into the vectorized form of its transpose. Specifically, the commutation matrix K^(m,n) is the nm × mn matrix which, for any m × n matrix A, transforms vec(A) into vec(A^T):

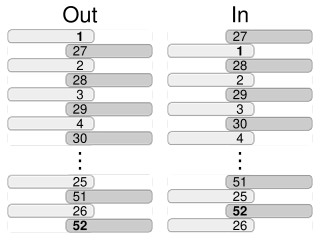
The faro shuffle (American), weave shuffle (British), or dovetail shuffle is a method of shuffling playing cards, in which half of the deck is held in each hand with the thumbs inward, then cards are released by the thumbs so that they fall to the table interleaved. Diaconis, Graham, and Kantor also call this the technique, when used in magic.

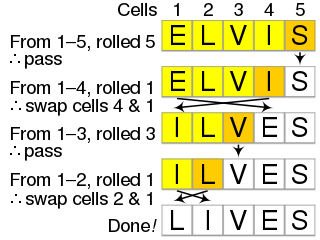
The Fisher–Yates shuffle is an algorithm for shuffling a finite sequence. The algorithm takes a list of all the elements of the sequence, and continually determines the next element in the shuffled sequence by randomly drawing an element from the list until no elements remain. The algorithm produces an unbiased permutation: every permutation is equally likely. The modern version of the algorithm takes time proportional to the number of items being shuffled and shuffles them in place.

In computer science and discrete mathematics, an inversion in a sequence is a pair of elements that are out of their natural order.

In mathematics, the Robinson–Schensted–Knuth correspondence, also referred to as the RSK correspondence or RSK algorithm, is a combinatorial bijection between matrices $A$ with non-negative integer entries and pairs $(P, Q)$ of semistandard Young tableaux of equal shape, whose size equals the sum of the entries of $A$ . More precisely the weight of $P$ is given by the column sums of $A$ , and the weight of $Q$ by its row sums. It is a generalization of the Robinson–Schensted correspondence, in the sense that taking $A$ to be a permutation matrix, the pair $(P, Q)$ will be the pair of standard tableaux associated to the permutation under the Robinson–Schensted correspondence.

In mathematics, particularly linear algebra, the Schur–Horn theorem, named after Issai Schur and Alfred Horn, characterizes the diagonal of a Hermitian matrix with given eigenvalues. It has inspired investigations and substantial generalizations in the setting of symplectic geometry. A few important generalizations are Kostant's convexity theorem, Atiyah–Guillemin–Sternberg convexity theorem, Kirwan convexity theorem.

In the mathematics of permutations and the study of shuffling playing cards, a riffle shuffle permutation is one of the permutations of a set of $items that can be obtained by a single riffle shuffle, in which a sorted deck of cards is cut into two packets and then the two packets are interleaved. Beginning with an ordered set, mathematically a riffle shuffle is defined as a permutation on this set containing 1 or 2 rising sequences. The permutations with 1 rising sequence are the identity permutations.$

In the mathematics of shuffling playing cards, the Gilbert–Shannon–Reeds model is a probability distribution on riffle shuffle permutations that has been reported to be a good match for experimentally observed outcomes of human shuffling, and that forms the basis for a recommendation that a deck of cards should be riffled seven times in order to thoroughly randomize it. It is named after the work of Edgar Gilbert, Claude Shannon, and J. Reeds, reported in a 1955 technical report by Gilbert and in a 1981 unpublished manuscript of Reeds.

<span class="mw-page-title-main">Topswops</span>

Topswops are mathematical problems devised and analysed by the British mathematician John Conway in 1973. Contrary to other games and problems introduced by Conway, these problems have not received much attention from the scientific community. Two famous mathematicians who have contributed to the problem are Martin Gardner and Donald Knuth.

Norman Laurence Gilbreath is an American magician and author known for originating the Gilbreath shuffle. He is also known for Gilbreath's conjecture concerning prime numbers.

References

1 2 3 4 5 6 7 Diaconis, Persi; Graham, Ron (2012), "Chapter 5: From the Gilbreath Principle to the Mandelbrot Set" (PDF), Magical Mathematics: the mathematical ideas that animate great magic tricks, Princeton University Press, pp. 61–83.
↑ Vella, Antoine (2002), "Pattern avoidance in permutations: linear and cyclic orders", Electronic Journal of Combinatorics, 9 (2): R18, doi: 10.37236/1690 , MR 2028287 . See in particular Proposition 3.3.
↑ Vella (2002) credits this result on the number of Gilbreath permutations to Simion, Rodica; Schmidt, Frank W. (1985), "Restricted permutations", European Journal of Combinatorics, 6 (4): 383–406, doi:10.1016/s0195-6698(85)80052-4, MR 0829358 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[dg-1] 1 2 3 4 5 6 7 Diaconis, Persi; Graham, Ron (2012), "Chapter 5: From the Gilbreath Principle to the Mandelbrot Set" (PDF), Magical Mathematics: the mathematical ideas that animate great magic tricks, Princeton University Press, pp. 61–83.

[v-2] Vella, Antoine (2002), "Pattern avoidance in permutations: linear and cyclic orders", Electronic Journal of Combinatorics, 9 (2): R18, doi: 10.37236/1690 , MR 2028287 . See in particular Proposition 3.3.

[3] Vella (2002) credits this result on the number of Gilbreath permutations to Simion, Rodica; Schmidt, Frank W. (1985), "Restricted permutations", European Journal of Combinatorics, 6 (4): 383–406, doi:10.1016/s0195-6698(85)80052-4, MR 0829358 .

[1]

[2]

[3]