Control theory is a field of control engineering and applied mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any delay, overshoot, or steady-state error and ensuring a level of control stability; often with the aim to achieve a degree of optimality.
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is derived from Ancient Greek ἴσος (isos) 'equal' and μορφή (morphe) 'form, shape'.
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event.
In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. Informally, a ring is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series.
Bell's theorem is a term encompassing a number of closely related results in physics, all of which determine that quantum mechanics is incompatible with local hidden-variable theories, given some basic assumptions about the nature of measurement. "Local" here refers to the principle of locality, the idea that a particle can only be influenced by its immediate surroundings, and that interactions mediated by physical fields cannot propagate faster than the speed of light. "Hidden variables" are supposed properties of quantum particles that are not included in quantum theory but nevertheless affect the outcome of experiments. In the words of physicist John Stewart Bell, for whom this family of results is named, "If [a hidden-variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local."
Negative feedback occurs when some function of the output of a system, process, or mechanism is fed back in a manner that tends to reduce the fluctuations in the output, whether caused by changes in the input or by other disturbances. A classic example of negative feedback is a heating system thermostat — when the temperature gets high enough, the heater is turned OFF. When the temperature gets too cold, the heat is turned back ON. In each case the "feedback" generated by the thermostat "negates" the trend.
In electronics, a linear regulator is a voltage regulator used to maintain a steady voltage. The resistance of the regulator varies in accordance with both the input voltage and the load, resulting in a constant voltage output. The regulating circuit varies its resistance, continuously adjusting a voltage divider network to maintain a constant output voltage and continually dissipating the difference between the input and regulated voltages as waste heat. By contrast, a switching regulator uses an active device that switches on and off to maintain an average value of output. Because the regulated voltage of a linear regulator must always be lower than input voltage, efficiency is limited and the input voltage must be high enough to always allow the active device to reduce the voltage by some amount.
William Ross Ashby was an English psychiatrist and a pioneer in cybernetics, the study of the science of communications and automatic control systems in both machines and living things. His first name was not used: he was known as Ross Ashby.
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “universal” group having these properties, in the sense that any two homomorphisms from G and H into a group K factor uniquely through a homomorphism from G ∗ H to K. Unless one of the groups G and H is trivial, the free product is always infinite. The construction of a free product is similar in spirit to the construction of a free group.
In universal algebra, a variety of algebras or equational class is the class of all algebraic structures of a given signature satisfying a given set of identities. For example, the groups form a variety of algebras, as do the abelian groups, the rings, the monoids etc. According to Birkhoff's theorem, a class of algebraic structures of the same signature is a variety if and only if it is closed under the taking of homomorphic images, subalgebras, and (direct) products. In the context of category theory, a variety of algebras, together with its homomorphisms, forms a category; these are usually called finitary algebraic categories.
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used.
In cybernetics and control theory, a setpoint is the desired or target value for an essential variable, or process value (PV) of a control system, which may differ from the actual measured value of the variable. Departure of such a variable from its setpoint is one basis for error-controlled regulation using negative feedback for automatic control. A setpoint can be any physical quantity or parameter that a control system seeks to regulate, such as temperature, pressure, flow rate, position, speed, or any other measurable attribute.
In metaphysics, a causal model is a conceptual model that describes the causal mechanisms of a system. Several types of causal notation may be used in the development of a causal model. Causal models can improve study designs by providing clear rules for deciding which independent variables need to be included/controlled for.
In cybernetics, the term variety denotes the total number of distinguishable elements of a set, most often the set of states, inputs, or outputs of a finite-state machine or transformation, or the binary logarithm of the same quantity. Variety is used in cybernetics as an information theory that is easily related to deterministic finite automata, and less formally as a conceptual tool for thinking about organization, regulation, and stability. It is an early theory of complexity in automata, complex systems, and operations research.
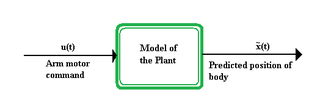
In the subject area of control theory, an internal model is a process that simulates the response of the system in order to estimate the outcome of a system disturbance. The internal model principle was first articulated in 1976 by B. A. Francis and W. M. Wonham as an explicit formulation of the Conant and Ashby good regulator theorem. It stands in contrast to classical control, in that the classical feedback loop fails to explicitly model the controlled system.
The free energy principle is a theoretical framework suggesting that the brain reduces surprise or uncertainty by making predictions based on internal models and updating them using sensory input. It highlights the brain's objective of aligning its internal model and the external world to enhance prediction accuracy. This principle integrates Bayesian inference with active inference, where actions are guided by predictions and sensory feedback refines them. It has wide-ranging implications for comprehending brain function, perception, and action.
Self-organization, a process where some form of overall order arises out of the local interactions between parts of an initially disordered system, was discovered in cybernetics by William Ross Ashby in 1947. It states that any deterministic dynamic system automatically evolves towards a state of equilibrium that can be described in terms of an attractor in a basin of surrounding states. Once there, the further evolution of the system is constrained to remain in the attractor. This constraint implies a form of mutual dependency or coordination between its constituent components or subsystems. In Ashby's terms, each subsystem has adapted to the environment formed by all other subsystems.
Mick Ashby's ethical regulator theorem builds upon the Conant-Ashby good regulator theorem, which is ambiguous because being good at regulating does not imply being good ethically.
Walter Murray Wonham was a Canadian control theorist and professor at the University of Toronto. He focused on multi-variable geometric control theory, stochastic control and stochastic filters, and the control of discrete event systems from the standpoint of mathematical logic and formal languages.
An Introduction to Cybernetics is a book by W. Ross Ashby, first published in 1956 in London by Chapman and Hall. An Introduction is considered the first textbook on cybernetics, where the basic principles of the new field were first rigorously laid out. It was intended to serve as an elementary introduction to cybernetic principles of homeostasis, primarily for an audience of physiologists, psychologists, and sociologists. Ashby addressed adjacent topics in addition to cybernetics such as information theory, communications theory, control theory, game theory and systems theory.
