In mathematics, the grand Riemann hypothesis is a generalisation of the Riemann hypothesis and generalized Riemann hypothesis. It states that the nontrivial zeros of all automorphic L-functions lie on the critical line with a real number variable and the imaginary unit.
The modified grand Riemann hypothesis is the assertion that the nontrivial zeros of all automorphic L-functions lie on the critical line or the real line.
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as
Louis de Branges de Bourcia is a French-American mathematician. He is the Edward C. Elliott Distinguished Professor of Mathematics at Purdue University in West Lafayette, Indiana. He is best known for proving the long-standing Bieberbach conjecture in 1984, now called de Branges's theorem. He claims to have proved several important conjectures in mathematics, including the generalized Riemann hypothesis.
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function. One can then ask the same question about the zeros of these L-functions, yielding various generalizations of the Riemann hypothesis. Many mathematicians believe these generalizations of the Riemann hypothesis to be true. The only cases of these conjectures which have been proven occur in the algebraic function field case.
In representation theory and algebraic number theory, the Langlands program is a web of far-reaching and consequential conjectures about connections between number theory and geometry. Proposed by Robert Langlands, it seeks to relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. Widely seen as the single biggest project in modern mathematical research, the Langlands program has been described by Edward Frenkel as "a kind of grand unified theory of mathematics."
In mathematics, the Weil conjectures were highly influential proposals by André Weil (1949). They led to a successful multi-decade program to prove them, in which many leading researchers developed the framework of modern algebraic geometry and number theory.
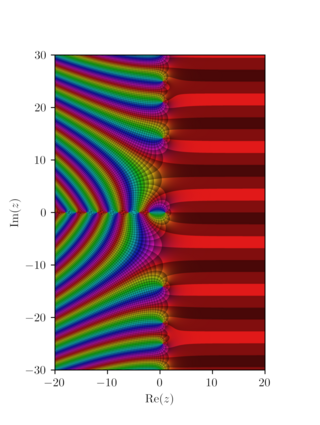
In mathematics, an L-function is a meromorphic function on the complex plane, associated to one out of several categories of mathematical objects. An L-series is a Dirichlet series, usually convergent on a half-plane, that may give rise to an L-function via analytic continuation. The Riemann zeta function is an example of an L-function, and one important conjecture involving L-functions is the Riemann hypothesis and its generalization.
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic progressions. It is well known for its results on prime numbers and additive number theory.
In mathematics, a Dirichlet L-series is a function of the form
In mathematics, the Hilbert–Pólya conjecture states that the non-trivial zeros of the Riemann zeta function correspond to eigenvalues of a self-adjoint operator. It is a possible approach to the Riemann hypothesis, by means of spectral theory.
In mathematics, the Ramanujan conjecture, due to Srinivasa Ramanujan (1916, p. 176), states that Ramanujan's tau function given by the Fourier coefficients τ(n) of the cusp form Δ(z) of weight 12
In mathematics, the Z function is a function used for studying the Riemann zeta function along the critical line where the argument is one-half. It is also called the Riemann–Siegel Z function, the Riemann–Siegel zeta function, the Hardy function, the Hardy Z function and the Hardy zeta function. It can be defined in terms of the Riemann–Siegel theta function and the Riemann zeta function by
In mathematics, the Lindelöf hypothesis is a conjecture by Finnish mathematician Ernst Leonard Lindelöf about the rate of growth of the Riemann zeta function on the critical line. This hypothesis is implied by the Riemann hypothesis. It says that for any ε > 0,
In mathematics, more specifically in the field of analytic number theory, a Landau–Siegel zero or simply Siegel zero, named after Edmund Landau and Carl Ludwig Siegel, is a type of potential counterexample to the generalized Riemann hypothesis, on the zeros of Dirichlet L-functions associated to quadratic number fields. Roughly speaking, these are possible zeros very near to .
In mathematics, the Selberg class is an axiomatic definition of a class of L-functions. The members of the class are Dirichlet series which obey four axioms that seem to capture the essential properties satisfied by most functions that are commonly called L-functions or zeta functions. Although the exact nature of the class is conjectural, the hope is that the definition of the class will lead to a classification of its contents and an elucidation of its properties, including insight into their relationship to automorphic forms and the Riemann hypothesis. The class was defined by Atle Selberg in, who preferred not to use the word "axiom" that later authors have employed.
Henryk Iwaniec is a Polish-American mathematician, and since 1987 a professor at Rutgers University. He is a member of the American Academy of Arts and Sciences and Polish Academy of Sciences. He has made important contributions to analytic and algebraic number theory as well as harmonic analysis. He is the recipient of Cole Prize (2002), Steele Prize (2011), and Shaw Prize (2015).
John Brian Conrey is an American mathematician and the executive director of the American Institute of Mathematics. His research interests are in number theory, specifically analysis of L-functions and the Riemann zeta function.
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann (1859), after whom it is named.
In mathematics, Montgomery's pair correlation conjecture is a conjecture made by Hugh Montgomery (1973) that the pair correlation between pairs of zeros of the Riemann zeta function is
The Millennium Prize Problems are seven well-known complex mathematical problems selected by the Clay Mathematics Institute in 2000. The Clay Institute has pledged a US$1 million prize for the first correct solution to each problem.
In mathematics, the arithmetic zeta function is a zeta function associated with a scheme of finite type over integers. The arithmetic zeta function generalizes the Riemann zeta function and Dedekind zeta function to higher dimensions. The arithmetic zeta function is one of the most-fundamental objects of number theory.
Conrey and Iwaniec show that sufficiently many small gaps between zeros of the Riemann zeta function would imply the non-existence of Landau–Siegel zeros.
 | This mathematical analysis–related article is a stub. You can help Wikipedia by expanding it. |
