Guillotine partition

Last updated May 24, 2024

A guillotine cutting: an optimised sheet of smaller rectangles which can be divided intact through the correct series of bisecting end-to-end cuts. CuttingStockGuillotine.png — A guillotine cutting: an optimised sheet of smaller rectangles which can be divided intact through the correct series of bisecting end-to-end cuts.

A non-guillotine cutting: these rectangles cannot be separated by making single bisecting cuts across the plane. CuttingStockNonGuillotine.png — A non-guillotine cutting: these rectangles *cannot* be separated by making single bisecting cuts across the plane.

Guillotine partition is the process of partitioning a rectilinear polygon, possibly containing some holes, into rectangles, using only guillotine-cuts. A guillotine-cut (also called an edge-to-edge cut) is a straight bisecting line going from one edge of an existing polygon to the opposite edge, similarly to a paper guillotine.

Guillotine partition is particularly common in designing floorplans in microelectronics. An alternative term for a guillotine-partition in this context is a slicing partition or a slicing floorplan.^[1] Guillotine partitions are also the underlying structure of binary space partitions. There are various optimization problems related to guillotine partition, such as: minimizing the number of rectangles or the total length of cuts. These are variants of polygon partitioning problems, where the cuts are constrained to be guillotine cuts.

A related but different problem is guillotine cutting . In that problem, the original sheet is a plain rectangle without holes. The challenge comes from the fact that the dimensions of the small rectangles are fixed in advance. The optimization goals are usually to maximize the area of the produced rectangles or their value, or minimize the waste or the number of required sheets.

Computing a guillotine partition with a smallest edge-length

In the minimum edge-length rectangular-partition problem, the goal is to partition the original rectilinear polygon into rectangles, such that the total edge length is a minimum.^[2]^{: 166–167}

This problem can be solved in time $O(n^{5})$ even if the raw polygon has holes. The algorithm uses dynamic programming based on the following observation: there exists a minimum-length guillotine rectangular partition in which every maximal line segment contains a vertex of the boundary. Therefore, in each iteration, there are $O(n)$ possible choices for the next guillotine cut, and there are altogether $O(n^{4})$ subproblems.

In the special case in which all holes are degenerate (single points), the minimum-length guillotine rectangular partition is at most 2 times the minimum-length rectangular partition.^[2]^{: 167–170} By a more careful analysis, it can be proved that the approximation factor is in fact at most 1.75. It is not known if the 1.75 is tight, but there is an instance in which the approximation factor is 1.5.^[3] Therefore, the guillotine partition provides a constant-factor approximation to the general problem, which is NP-hard.

These results can be extended to a d-dimensional box: a guillotine-partition with minimum edge-length can be found in time $O(dn^{2d+1})$ , and the total (d-1)-volume in the optimal guillotine-partition is at most $2d-4+4/d$ times that of an optimal d-box partition.^[4]

Arora^[5] and Mitchell^[6] used the guillotine-partitioning technique to develop polynomial-time approximation schemes for various geometric optimization problems.

Number of guillotine partitions

Besides the computational problems, guillotine partitions were also studied from a combinatorial perspective. Suppose a given rectangle should be partitioned into smaller rectangles using guillotine cuts only. Obviously, there are infinitely many ways to do this, since even a single cut can take infinitely many values. However, the number of structurally-different guillotine partitions is bounded.

In two dimensions, there is an upper bound in $O\left({\frac {n!2^{5n-3}}{n^{3/2}}}\right)$ attributed to Knuth. the exact number is the Schröder number.^[7]
In d dimensions, Ackerman, Barequet, Pinter and Romik^[8] give an exact summation formula, and prove that it is in $\Theta \left({\frac {(2d-1+2{\sqrt {d(d-1)}})^{n}}{n^{3/2}}}\right)$ . When d=2 this bound becomes $\Theta \left({\frac {(3+2{\sqrt {2}})^{n}}{n^{3/2}}}\right)$ .
Asinowski, Barequet, Mansour and Pinter^[9] also study the number of cut-equivalence classes of guillotine partitions.

Coloring guillotine partitions

A polychromatic coloring of a planar graph is a coloring of its vertices such that, in each face of the graph, each color appears at least once. Several researchers have tried to find the largest k such that a polychromatic k-coloring always exists. An important special case is when the graph represents a partition of a rectangle into rectangles.

Dinitz, Katz and Krakovski^[10] proved that there always exists a polychromatic 3-coloring.
Aigner-Horev, Katz, Krakovski and Loffler^[11] proved that, in the special sub-case in which the graph represents a guillotine partition, a strong polychromatic 4-coloring always exists.
Keszegh^[12] extended this result to d-dimensional guillotine partitions, and provided an efficient coloring algorithm.
Dimitrov, Aigner-Horev and Krakovski^[13] finally proved that there always exists a strong polychromatic 4-coloring.

Related Research Articles

The bin packing problem is an optimization problem, in which items of different sizes must be packed into a finite number of bins or containers, each of a fixed given capacity, in a way that minimizes the number of bins used. The problem has many applications, such as filling up containers, loading trucks with weight capacity constraints, creating file backups in media, and technology mapping in FPGA semiconductor chip design.

In graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set $of vertices such that for every two vertices in, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in . A set is independent if and only if it is a clique in the graph's complement. The size of an independent set is the number of vertices it contains. Independent sets have also been called "internally stable sets", of which "stable set" is a shortening.$

In graph theory, a complete coloring is a vertex coloring in which every pair of colors appears on at least one pair of adjacent vertices. Equivalently, a complete coloring is minimal in the sense that it cannot be transformed into a proper coloring with fewer colors by merging pairs of color classes. The achromatic number $ψ(G)$ of a graph $G$ is the maximum number of colors possible in any complete coloring of $G$ .

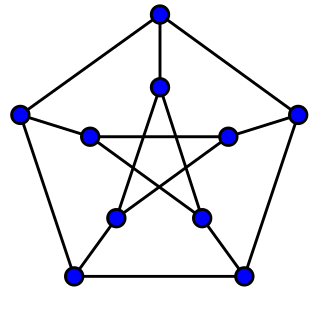
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

The art gallery problem or museum problem is a well-studied visibility problem in computational geometry. It originates from the following real-world problem:

"In an art gallery, what is the minimum number of guards who together can observe the whole gallery?"

In information visualization and computing, treemapping is a method for displaying hierarchical data using nested figures, usually rectangles.

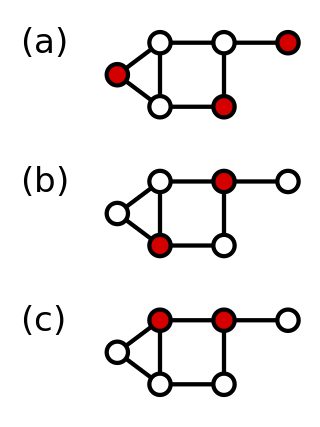
<span class="mw-page-title-main">Dominating set</span> Subset of a graphs nodes such that all other nodes link to at least one

In graph theory, a dominating set for a graph $G$ is a subset $D$ of its vertices, such that any vertex of $G$ is in $D$ , or has a neighbor in $D$ . The domination number $γ(G)$ is the number of vertices in a smallest dominating set for $G$ .

In graph theory, a domatic partition of a graph $is a partition of into disjoint sets,,..., such that each V i is a dominating set for G . The figure on the right shows a domatic partition of a graph; here the dominating set consists of the yellow vertices, consists of the green vertices, and consists of the blue vertices.$

<span class="mw-page-title-main">Guillotine cutting</span> Process of producing small rectangular items of fixed dimensions

Guillotine cutting is the process of producing small rectangular items of fixed dimensions from a given large rectangular sheet, using only guillotine-cuts. A guillotine-cut is a straight bisecting line going from one edge of an existing rectangle to the opposite edge, similarly to a paper guillotine.

In computational geometry, the smallest enclosing box problem is that of finding the oriented minimum bounding box enclosing a set of points. It is a type of bounding volume. "Smallest" may refer to volume, area, perimeter, etc. of the box.

In mathematics, the minimum $k$ -cut is a combinatorial optimization problem that requires finding a set of edges whose removal would partition the graph to at least $k$ connected components. These edges are referred to as $k$ -cut. The goal is to find the minimum-weight $k$ -cut. This partitioning can have applications in VLSI design, data-mining, finite elements and communication in parallel computing.

In computational geometry, a maximum disjoint set (MDS) is a largest set of non-overlapping geometric shapes selected from a given set of candidate shapes.

In the geometry of the Euclidean plane, axiality is a measure of how much axial symmetry a shape has. It is defined as the ratio of areas of the largest axially symmetric subset of the shape to the whole shape. Equivalently it is the largest fraction of the area of the shape that can be covered by a mirror reflection of the shape.

In geometry, a covering of a polygon is a set of primitive units whose union equals the polygon. A polygon covering problem is a problem of finding a covering with a smallest number of units for a given polygon. This is an important class of problems in computational geometry. There are many different polygon covering problems, depending on the type of polygon being covered. An example polygon covering problem is: given a rectilinear polygon, find a smallest set of squares whose union equals the polygon.

In geometry, a partition of a polygon is a set of primitive units, which do not overlap and whose union equals the polygon. A polygon partition problem is a problem of finding a partition which is minimal in some sense, for example a partition with a smallest number of units or with units of smallest total side-length.

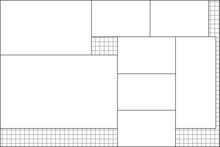
The strip packing problem is a 2-dimensional geometric minimization problem. Given a set of axis-aligned rectangles and a strip of bounded width and infinite height, determine an overlapping-free packing of the rectangles into the strip, minimizing its height. This problem is a cutting and packing problem and is classified as an Open Dimension Problem according to Wäscher et al.

Rectangle packing is a packing problem where the objective is to determine whether a given set of small rectangles can be placed inside a given large polygon, such that no two small rectangles overlap. Several variants of this problem have been studied.

Identical-machines scheduling is an optimization problem in computer science and operations research. We are given n jobs J₁, J₂, ..., J_n of varying processing times, which need to be scheduled on m identical machines, such that a certain objective function is optimized, for example, the makespan is minimized.

In graph theory, the cutwidth of an undirected graph is the smallest integer $with the following property: there is an ordering of the vertices of the graph, such that every cut obtained by partitioning the vertices into earlier and later subsets of the ordering is crossed by at most edges. That is, if the vertices are numbered, then for every, the number of edges with and is at most .$

References

↑ Lengauer, Thomas (1990), "Circuit Partitioning", Combinatorial Algorithms for Integrated Circuit Layout, Wiesbaden: Vieweg+Teubner Verlag, pp. 251–301, doi:10.1007/978-3-322-92106-2_6, ISBN 978-3-322-92108-6 , retrieved 2021-01-16
1 2 Du, Ding-Zhu; Ko, Ker-I.; Hu, Xiaodong (2012). Design and Analysis of Approximation Algorithms. Springer Optimization and Its Applications. New York: Springer-Verlag. pp. 165–209, chapter 5 "guillotine cut". ISBN 978-1-4614-1700-2.
↑ Gonzalez, Teofilo; Zheng, Si-Qing (1989-06-01). "Improved bounds for rectangular and guillotine partitions". Journal of Symbolic Computation. 7 (6): 591–610. doi: 10.1016/S0747-7171(89)80042-2 . ISSN 0747-7171.
↑ Gonzalez, Teofilo F.; Razzazi, Mohammadreza; Shing, Man-Tak; Zheng, Si-Qing (1994-05-01). "On optimal guillotine partitions approximating optimal d-box partitions". Computational Geometry . 4 (1): 1–11. doi: 10.1016/0925-7721(94)90013-2 . ISSN 0925-7721.
↑ Arora, S. (October 1996). "Polynomial time approximation schemes for Euclidean TSP and other geometric problems". Proceedings of 37th Conference on Foundations of Computer Science. pp. 2–11. doi:10.1109/SFCS.1996.548458. ISBN 0-8186-7594-2. S2CID 1499391.
↑ Mitchell, Joseph S. B. (1999-01-01). "Guillotine Subdivisions Approximate Polygonal Subdivisions: A Simple Polynomial-Time Approximation Scheme for Geometric TSP, k-MST, and Related Problems". SIAM Journal on Computing. 28 (4): 1298–1309. doi:10.1137/S0097539796309764. ISSN 0097-5397.
↑ Yao, Bo; Chen, Hongyu; Cheng, Chung-Kuan; Graham, Ronald (2003-01-01). "Floorplan representations: Complexity and connections". ACM Transactions on Design Automation of Electronic Systems. 8 (1): 55–80. doi:10.1145/606603.606607. ISSN 1084-4309. S2CID 1645358.
↑ Ackerman, Eyal; Barequet, Gill; Pinter, Ron Y.; Romik, Dan (2006-05-31). "The number of guillotine partitions in d dimensions". Information Processing Letters. 98 (4): 162–167. doi:10.1016/j.ipl.2006.01.011. ISSN 0020-0190.
↑ Asinowski, Andrei; Barequet, Gill; Mansour, Toufik; Pinter, Ron Y. (2014-09-28). "Cut equivalence of d-dimensional guillotine partitions". Discrete Mathematics . 331: 165–174. doi: 10.1016/j.disc.2014.05.014 . ISSN 0012-365X.
↑ Dinitz, Yefim; Katz, Matthew J.; Krakovski, Roi (2009-12-01). "Guarding rectangular partitions". International Journal of Computational Geometry & Applications. 19 (6): 579–594. doi:10.1142/S0218195909003131. ISSN 0218-1959.
↑ Horev, Elad; Katz, Matthew J.; Krakovski, Roi; Löffler, Maarten (2009-06-15). "Polychromatic 4-coloring of guillotine subdivisions". Information Processing Letters. 109 (13): 690–694. doi:10.1016/j.ipl.2009.03.006. ISSN 0020-0190.
↑ Keszegh, Balázs (2008). Hu, Xiaodong; Wang, Jie (eds.). "Polychromatic Colorings of n-Dimensional Guillotine-Partitions". Computing and Combinatorics. Lecture Notes in Computer Science. 5092. Berlin, Heidelberg: Springer: 110–118. doi:10.1007/978-3-540-69733-6_12. ISBN 978-3-540-69733-6.
↑ Dimitrov, Darko; Horev, Elad; Krakovski, Roi (2009-05-06). "Polychromatic colorings of rectangular partitions". Discrete Mathematics . 309 (9): 2957–2960. doi: 10.1016/j.disc.2008.07.035 . ISSN 0012-365X.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Lengauer, Thomas (1990), "Circuit Partitioning", Combinatorial Algorithms for Integrated Circuit Layout, Wiesbaden: Vieweg+Teubner Verlag, pp. 251–301, doi:10.1007/978-3-322-92106-2_6, ISBN 978-3-322-92108-6 , retrieved 2021-01-16

[:0-2] 1 2 Du, Ding-Zhu; Ko, Ker-I.; Hu, Xiaodong (2012). Design and Analysis of Approximation Algorithms. Springer Optimization and Its Applications. New York: Springer-Verlag. pp. 165–209, chapter 5 "guillotine cut". ISBN 978-1-4614-1700-2.

[3] Gonzalez, Teofilo; Zheng, Si-Qing (1989-06-01). "Improved bounds for rectangular and guillotine partitions". Journal of Symbolic Computation. 7 (6): 591–610. doi: 10.1016/S0747-7171(89)80042-2 . ISSN 0747-7171.

[:6-4] Gonzalez, Teofilo F.; Razzazi, Mohammadreza; Shing, Man-Tak; Zheng, Si-Qing (1994-05-01). "On optimal guillotine partitions approximating optimal d-box partitions". Computational Geometry . 4 (1): 1–11. doi: 10.1016/0925-7721(94)90013-2 . ISSN 0925-7721.

[5] Arora, S. (October 1996). "Polynomial time approximation schemes for Euclidean TSP and other geometric problems". Proceedings of 37th Conference on Foundations of Computer Science. pp. 2–11. doi:10.1109/SFCS.1996.548458. ISBN 0-8186-7594-2. S2CID 1499391.

[6] Mitchell, Joseph S. B. (1999-01-01). "Guillotine Subdivisions Approximate Polygonal Subdivisions: A Simple Polynomial-Time Approximation Scheme for Geometric TSP, k-MST, and Related Problems". SIAM Journal on Computing. 28 (4): 1298–1309. doi:10.1137/S0097539796309764. ISSN 0097-5397.

[7] Yao, Bo; Chen, Hongyu; Cheng, Chung-Kuan; Graham, Ronald (2003-01-01). "Floorplan representations: Complexity and connections". ACM Transactions on Design Automation of Electronic Systems. 8 (1): 55–80. doi:10.1145/606603.606607. ISSN 1084-4309. S2CID 1645358.

[8] Ackerman, Eyal; Barequet, Gill; Pinter, Ron Y.; Romik, Dan (2006-05-31). "The number of guillotine partitions in d dimensions". Information Processing Letters. 98 (4): 162–167. doi:10.1016/j.ipl.2006.01.011. ISSN 0020-0190.

[9] Asinowski, Andrei; Barequet, Gill; Mansour, Toufik; Pinter, Ron Y. (2014-09-28). "Cut equivalence of d-dimensional guillotine partitions". Discrete Mathematics . 331: 165–174. doi: 10.1016/j.disc.2014.05.014 . ISSN 0012-365X.

[10] Dinitz, Yefim; Katz, Matthew J.; Krakovski, Roi (2009-12-01). "Guarding rectangular partitions". International Journal of Computational Geometry & Applications. 19 (6): 579–594. doi:10.1142/S0218195909003131. ISSN 0218-1959.

[11] Horev, Elad; Katz, Matthew J.; Krakovski, Roi; Löffler, Maarten (2009-06-15). "Polychromatic 4-coloring of guillotine subdivisions". Information Processing Letters. 109 (13): 690–694. doi:10.1016/j.ipl.2009.03.006. ISSN 0020-0190.

[12] Keszegh, Balázs (2008). Hu, Xiaodong; Wang, Jie (eds.). "Polychromatic Colorings of n-Dimensional Guillotine-Partitions". Computing and Combinatorics. Lecture Notes in Computer Science. 5092. Berlin, Heidelberg: Springer: 110–118. doi:10.1007/978-3-540-69733-6_12. ISBN 978-3-540-69733-6.

[13] Dimitrov, Darko; Horev, Elad; Krakovski, Roi (2009-05-06). "Polychromatic colorings of rectangular partitions". Discrete Mathematics . 309 (9): 2957–2960. doi: 10.1016/j.disc.2008.07.035 . ISSN 0012-365X.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]