
John Horton Conway was an English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many branches of recreational mathematics, most notably the invention of the cellular automaton called the Game of Life.

The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is a zero-player game, meaning that its evolution is determined by its initial state, requiring no further input. One interacts with the Game of Life by creating an initial configuration and observing how it evolves. It is Turing complete and can simulate a universal constructor or any other Turing machine.

A cellular automaton is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling.

Ralph William Gosper Jr., known as Bill Gosper, is an American mathematician and programmer. Along with Richard Greenblatt, he may be considered to have founded the hacker community, and he holds a place of pride in the Lisp community. The Gosper curve and the Gosper's algorithm are named after him.

Highlife is a cellular automaton similar to Conway's Game of Life. It was devised in 1994 by Nathan Thompson. It is a two-dimensional, two-state cellular automaton in the "Life family" and is described by the rule B36/S23; that is, a cell is born if it has 3 or 6 neighbors and survives if it has 2 or 3 neighbors. Because the rules of HighLife and Conway's Life are similar, many simple patterns in Conway's Life function identically in HighLife. More complicated engineered patterns for one rule, though, typically do not work in the other rule.

In a cellular automaton, a finite pattern is called a spaceship if it reappears after a certain number of generations in the same orientation but in a different position. The smallest such number of generations is called the period of the spaceship.
In a cellular automaton, a puffer train, or simply puffer, is a finite pattern that moves itself across the "universe", leaving debris behind. Thus a pattern consisting of only a puffer will grow arbitrarily large over time. While both puffers and spaceships have periods and speeds, unlike puffers, spaceships do not leave debris behind.
A cellular automaton (CA) is Life-like if it meets the following criteria:

Day and Night is a cellular automaton rule in the same family as Game of Life. It is defined by rule notation B3678/S34678, meaning that a dead cell becomes live if it has 3, 6, 7, or 8 live neighbors, and a live cell remains alive (survives) if it has 3, 4, 6, 7, or 8 live neighbors, out of the eight neighbors in the Moore neighborhood. It was invented and named by Nathan Thompson in 1997, and investigated extensively by David I. Bell. The rule is given the name "Day & Night" because its on and off states are symmetric: if all the cells in the Universe are inverted, the future states are the inversions of the future states of the original pattern. A pattern in which the entire universe consists of off cells except for finitely many on cells can equivalently be represented by a pattern in which the whole universe is covered in on cells except for finitely many off cells in congruent locations.
Hashlife is a memoized algorithm for computing the long-term fate of a given starting configuration in Conway's Game of Life and related cellular automata, much more quickly than would be possible using alternative algorithms that simulate each time step of each cell of the automaton. The algorithm was first described by Bill Gosper in the early 1980s while he was engaged in research at the Xerox Palo Alto Research Center. Hashlife was originally implemented on Symbolics Lisp machines with the aid of the Flavors extension.
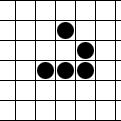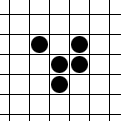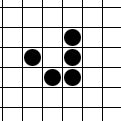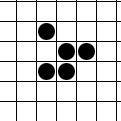
The glider is a pattern that travels across the board in Conway's Game of Life. It was first discovered by Richard K. Guy in 1969, while John Conway's group was attempting to track the evolution of the R-pentomino. Gliders are the smallest spaceships, and they travel diagonally at a speed of one cell every four generations, or . The glider is often produced from randomly generated starting configurations.

In cellular automata, a methuselah is a small "seed" pattern of initial live cells that take a large number of generations in order to stabilize. More specifically, Martin Gardner defines them as patterns of fewer than ten live cells which take longer than 50 generations to stabilize, although some patterns that are larger than ten cells have also been called methuselahs. Patterns must eventually stabilize to be considered methuselahs. The term comes from the Biblical Methuselah, who lived for 969 years.
In Conway's Game of Life and other cellular automata, a still life is a pattern that does not change from one generation to the next. The term comes from the art world where a still life painting or photograph depicts an inanimate scene. In cellular automata, a still life can be thought of as an oscillator with unit period.

A rake, in the lexicon of cellular automata, is a type of puffer train, which is an automaton that leaves behind a trail of debris. In the case of a rake, however, the debris left behind is a stream of spaceships, which are automata that "travel" by looping through a short series of iterations and end up in a new location after each cycle returns to the original configuration.

In Conway's Game of Life and similar cellular automaton rules, a spark is a small collection of live cells that appears at the edge of some larger pattern such as a spaceship or oscillator, then quickly dies off.
In Conway's Game of Life, the speed of light is a propagation rate across the grid of exactly one step per generation. In a single generation, a cell can only influence its nearest neighbours, and so the speed of light is the maximum rate at which information can propagate. It is therefore an upper bound to the speed at which any pattern can move.

Brian's Brain is a cellular automaton devised by Brian Silverman, which is very similar to his Seeds rule.

Life without Death is a cellular automaton, similar to Conway's Game of Life and other Life-like cellular automaton rules. In this cellular automaton, an initial seed pattern grows according to the same rule as in Conway's Game of Life; however, unlike Life, patterns never shrink. The rule was originally considered by Toffoli & Margolus (1987), who called it "Inkspot"; it has also been called "Flakes". In contrast to the more complex patterns that exist within Conway's Game of Life, Life without Death commonly features still life patterns, in which no change occurs, and ladder patterns, that grow in a straight line.

In Conway's Game of Life and related cellular automata, a spacefiller is a pattern that spreads out indefinitely, eventually filling the entire space with a still life pattern. It typically consists of three components: stretchers that resemble spaceships at the four corners of the pattern, a growing boundary region along the edges of the pattern, and the still life in the interior pattern.

Critters is a reversible block cellular automaton with similar dynamics to Conway's Game of Life, first described by Tommaso Toffoli and Norman Margolus in 1987.

















