In cellular automata, a replicator is a pattern that produces copies of itself.
In the one-dimensional Rule 90 cellular automaton, every pattern is a replicator. [1] The same is true in the life-like cellular automaton rule Replicator (B1357/S1357). [2] [3]
Highlife (B36/S23) rule has a simple replicator. [2]
On November 23, 2013, Dave Greene built the first replicator in Conway's Game of Life (B3/S23). [4] [ better source needed ]
The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is a zero-player game, meaning that its evolution is determined by its initial state, requiring no further input. One interacts with the Game of Life by creating an initial configuration and observing how it evolves. It is Turing complete and can simulate a universal constructor or any other Turing machine.
A cellular automaton is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling.
The Rule 110 cellular automaton is an elementary cellular automaton with interesting behavior on the boundary between stability and chaos. In this respect, it is similar to Conway's Game of Life. Like Life, Rule 110 with a particular repeating background pattern is known to be Turing complete. This implies that, in principle, any calculation or computer program can be simulated using this automaton.
Highlife is a cellular automaton similar to Conway's Game of Life. It was devised in 1994 by Nathan Thompson. It is a two-dimensional, two-state cellular automaton in the "Life family" and is described by the rule B36/S23; that is, a cell is born if it has 3 or 6 neighbors and survives if it has 2 or 3 neighbors. Because the rules of HighLife and Conway's Life are similar, many simple patterns in Conway's Life function identically in HighLife. More complicated engineered patterns for one rule, though, typically do not work in the other rule.
A cellular automaton (CA) is Life-like if it meets the following criteria:
Seeds is a cellular automaton in the same family as the Game of Life, initially investigated by Brian Silverman and named by Mirek Wójtowicz. It consists of an infinite two-dimensional grid of cells, each of which may be in one of two states: on or off. Each cell is considered to have eight neighbors, as in Life. In each time step, a cell turns on or is "born" if it was off or "dead" but had exactly two neighbors that were on; all other cells turn off. Thus, in the notation describing the family of cellular automata containing Life, it is described by the rule B2/S.
In a cellular automaton, a Garden of Eden is a configuration that has no predecessor. It can be the initial configuration of the automaton but cannot arise in any other way. John Tukey named these configurations after the Garden of Eden in Abrahamic religions, which was created out of nowhere.
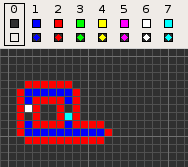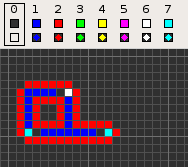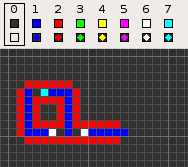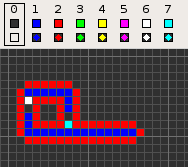
Codd's cellular automaton is a cellular automaton (CA) devised by the British computer scientist Edgar F. Codd in 1968. It was designed to recreate the computation- and construction-universality of von Neumann's CA but with fewer states: 8 instead of 29. Codd showed that it was possible to make a self-reproducing machine in his CA, in a similar way to von Neumann's universal constructor, but never gave a complete implementation.
A block cellular automaton or partitioning cellular automaton is a special kind of cellular automaton in which the lattice of cells is divided into non-overlapping blocks and the transition rule is applied to a whole block at a time rather than a single cell. Block cellular automata are useful for simulations of physical quantities, because it is straightforward to choose transition rules that obey physical constraints such as reversibility and conservation laws.
A cyclic cellular automaton is a kind of cellular automaton rule developed by David Griffeath and studied by several other cellular automaton researchers. In this system, each cell remains unchanged until some neighboring cell has a modular value exactly one unit larger than that of the cell itself, at which point it copies its neighbor's value. One-dimensional cyclic cellular automata can be interpreted as systems of interacting particles, while cyclic cellular automata in higher dimensions exhibit complex spiraling behavior.
Langton's loops are a particular "species" of artificial life in a cellular automaton created in 1984 by Christopher Langton. They consist of a loop of cells containing genetic information, which flows continuously around the loop and out along an "arm", which will become the daughter loop. The "genes" instruct it to make three left turns, completing the loop, which then disconnects from its parent.
A rake, in the lexicon of cellular automata, is a type of puffer train, which is an automaton that leaves behind a trail of debris. In the case of a rake, however, the debris left behind is a stream of spaceships, which are automata that "travel" by looping through a short series of iterations and end up in a new location after each cycle returns to the original configuration.
John von Neumann's universal constructor is a self-replicating machine in a cellular automaton (CA) environment. It was designed in the 1940s, without the use of a computer. The fundamental details of the machine were published in von Neumann's book Theory of Self-Reproducing Automata, completed in 1966 by Arthur W. Burks after von Neumann's death. While typically not as well known as von Neumann's other work, it is regarded as foundational for automata theory, complex systems, and artificial life. Indeed, Nobel Laureate Sydney Brenner considered Von Neumann's work on self-reproducing automata central to biological theory as well, allowing us to "discipline our thoughts about machines, both natural and artificial."
Cellular automata, as with other multi-agent system models, usually treat time as discrete and state updates as occurring synchronously. The state of every cell in the model is updated together, before any of the new states influence other cells. In contrast, an asynchronous cellular automaton is able to update individual cells independently, in such a way that the new state of a cell affects the calculation of states in neighbouring cells.
In the mathematical study of cellular automata, Rule 90 is an elementary cellular automaton based on the exclusive or function. It consists of a one-dimensional array of cells, each of which can hold either a 0 or a 1 value. In each time step all values are simultaneously replaced by the exclusive or of their two neighboring values. Martin, Odlyzko & Wolfram (1984) call it "the simplest non-trivial cellular automaton", and it is described extensively in Stephen Wolfram's 2002 book A New Kind of Science.
The Byl's loop is an artificial lifeform similar in concept to Langton's loop. It is a two-dimensional, 5-neighbor cellular automaton with 6 states per cell, and was developed in 1989 by John Byl, from the Department of Mathematical Sciences of Trinity Western University.
Brian's Brain is a cellular automaton devised by Brian Silverman, which is very similar to his Seeds rule.
In a cellular automaton, a finite pattern is called a sawtooth if its population grows without bound but does not tend to infinity. In other words, a sawtooth is a pattern with population that reaches new heights infinitely often, but also infinitely often drops below some fixed value. Their name comes from the fact that their plot of population versus generation number looks roughly like an ever-increasing sawtooth wave.
Life without Death is a cellular automaton, similar to Conway's Game of Life and other Life-like cellular automaton rules. In this cellular automaton, an initial seed pattern grows according to the same rule as in Conway's Game of Life; however, unlike Life, patterns never shrink. The rule was originally considered by Toffoli & Margolus (1987), who called it "Inkspot"; it has also been called "Flakes". In contrast to the more complex patterns that exist within Conway's Game of Life, Life without Death commonly features still life patterns, in which no change occurs, and ladder patterns, that grow in a straight line.
A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood.
 | This computer science article is a stub. You can help Wikipedia by expanding it. |