
The Herzberger Quader is a solid dissection puzzle invented by German mathematics teacher Gerhard Schulze. [1] It was named after his home-town Herzberg, and Quader is the latin-derived German word for a rectangular cuboid.

The Herzberger Quader is a solid dissection puzzle invented by German mathematics teacher Gerhard Schulze. [1] It was named after his home-town Herzberg, and Quader is the latin-derived German word for a rectangular cuboid.

The Herzberger Quader consists of a set of all possible polycubes from dicube to tetracubes. [2] The eleven pieces together have 40 unit cubes and thus can be stored in a 2 × 4 × 5 box. [2]
Besides stowing the Herzberger Quader in its box there are a lot of figures that can be built using all parts. Various subsets can be used to form a 3 × 3 × 3 cube, one of them is the famous Soma cube. [2]
Much more demanding tasks ask for the number of all different possibilities to arrange the initial parts in a certain figure. Or proofs are to be given for which figures can be realized or not realized with which polycubes. [2]
Author of the Herzberger Quader is Oberstudienrat Gerhard Schulze (1919–1995), who was intensively engaged in mathematical games during his extracurricular activities in the years 1982–1994. [3] On the occasion of the 800th anniversary of his hometown Herzberg in 1984, the Herzberger Quader was produced for the first time and thus made known to a broad public. Today, the Herzberger Quader is suggested to be used in the context of mathematics education. [4] [5]

In geometry, a cube is a three-dimensional solid object bounded by six square faces. It has twelve edges and eight vertices. It can be represented as a rectangular cuboid with six square faces, or a parallelepiped with equal edges. It is an example of many type of solids: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron.
In geometry, a tetrahedron, also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra.
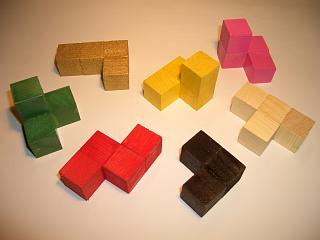
The Soma cube is a solid dissection puzzle invented by Danish polymath Piet Hein in 1933 during a lecture on quantum mechanics conducted by Werner Heisenberg.

Gerhard Karl Erich Gentzen was a German mathematician and logician. He made major contributions to the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus. He died of starvation in a Czech prison camp in Prague in 1945, having been interned as a German national after the Second World War.

In common usage, the abscissa refers to the x coordinate and the ordinate refers to the y coordinate of a standard two-dimensional graph.
In mathematical logic, a sequent is a very general kind of conditional assertion.
In mathematics, a multiset is a modification of the concept of a set that, unlike a set, allows for multiple instances for each of its elements. The number of instances given for each element is called the multiplicity of that element in the multiset. As a consequence, an infinite number of multisets exist which contain only elements a and b, but vary in the multiplicities of their elements:
In mathematical logic, descriptive set theory (DST) is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces. As well as being one of the primary areas of research in set theory, it has applications to other areas of mathematics such as functional analysis, ergodic theory, the study of operator algebras and group actions, and mathematical logic.

Blockout is a puzzle video game published in 1989 by California Dreams. It was developed in Poland by Aleksander Ustaszewski and Mirosław Zabłocki. American Technos published an arcade version. Blockout is an unlicensed, 3D version of Tetris.

A polycube is a solid figure formed by joining one or more equal cubes face to face. Polycubes are the three-dimensional analogues of the planar polyominoes. The Soma cube, the Bedlam cube, the Diabolical cube, the Slothouber–Graatsma puzzle, and the Conway puzzle are examples of packing problems based on polycubes.
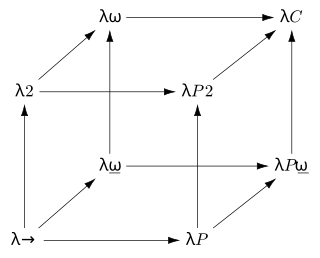
In mathematical logic and type theory, the λ-cube is a framework introduced by Henk Barendregt to investigate the different dimensions in which the calculus of constructions is a generalization of the simply typed λ-calculus. Each dimension of the cube corresponds to a new kind of dependency between terms and types. Here, "dependency" refers to the capacity of a term or type to bind a term or type. The respective dimensions of the λ-cube correspond to:

In geometry, the rhombille tiling, also known as tumbling blocks, reversible cubes, or the dice lattice, is a tessellation of identical 60° rhombi on the Euclidean plane. Each rhombus has two 60° and two 120° angles; rhombi with this shape are sometimes also called diamonds. Sets of three rhombi meet at their 120° angles, and sets of six rhombi meet at their 60° angles.
In cryptography, higher-order differential cryptanalysis is a generalization of differential cryptanalysis, an attack used against block ciphers. While in standard differential cryptanalysis the difference between only two texts is used, higher-order differential cryptanalysis studies the propagation of a set of differences between a larger set of texts. Xuejia Lai, in 1994, laid the groundwork by showing that differentials are a special case of the more general case of higher order derivates. Lars Knudsen, in the same year, was able to show how the concept of higher order derivatives can be used to mount attacks on block ciphers. These attacks can be superior to standard differential cryptanalysis. Higher-order differential cryptanalysis has notably been used to break the KN-Cipher, a cipher which had previously been proved to be immune against standard differential cryptanalysis.
In geometry, a near-miss Johnson solid is a strictly convex polyhedron whose faces are close to being regular polygons but some or all of which are not precisely regular. Thus, it fails to meet the definition of a Johnson solid, a polyhedron whose faces are all regular, though it "can often be physically constructed without noticing the discrepancy" between its regular and irregular faces. The precise number of near-misses depends on how closely the faces of such a polyhedron are required to approximate regular polygons.

The Slothouber–Graatsma puzzle is a packing problem that calls for packing six 1 × 2 × 2 blocks and three 1 × 1 × 1 blocks into a 3 × 3 × 3 box. The solution to this puzzle is unique. It was named after its inventors Jan Slothouber and William Graatsma.

Deutsche Mathematik was a mathematics journal founded in 1936 by Ludwig Bieberbach and Theodor Vahlen. Vahlen was publisher on behalf of the German Research Foundation (DFG), and Bieberbach was chief editor. Other editors were Fritz Kubach, Erich Schönhardt, Werner Weber, Ernst August Weiß, Karl Dörge, Wilhelm Süss, Günther Schulz (de), Erhard Tornier, Georg Feigl, Gerhard Kowalewski, Maximilian Krafft, Willi Rinow, Max Zacharias, and Oswald Teichmüller. In February 1936, the journal was declared the official organ of the German Student Union (DSt) by its Reichsführer, and all local DSt mathematics departments were requested to subscribe and actively contribute. In the 1940s, issues appeared increasingly delayed and bunched; the journal ended with a triple issue in June 1944.

Erika Pannwitz was a German mathematician who worked in the area of geometric topology. During World War II, Pannwitz worked as a cryptanalyst in the Department of Signal Intelligence Agency of the German Foreign Office colloquially known as Pers Z S. After the war, she became editor-in-chief of Zentralblatt MATH.

Maximilian Jacob Herzberger was a German-American mathematician and physicist, known for his development of the superachromat lens.

Bronshtein and Semendyayev is the informal name of a comprehensive handbook of fundamental working knowledge of mathematics and table of formulas originally compiled by the Russian mathematician Ilya Nikolaevich Bronshtein and engineer Konstantin Adolfovic Semendyayev.
Algebra and Tiling: Homomorphisms in the Service of Geometry is a mathematics textbook on the use of group theory to answer questions about tessellations and higher dimensional honeycombs, partitions of the Euclidean plane or higher-dimensional spaces into congruent tiles. It was written by Sherman K. Stein and Sándor Szabó, and published by the Mathematical Association of America as volume 25 of their Carus Mathematical Monographs series in 1994. It won the 1998 Beckenbach Book Prize, and was reprinted in paperback in 2008.