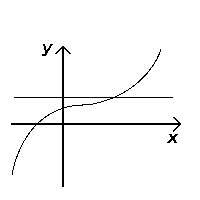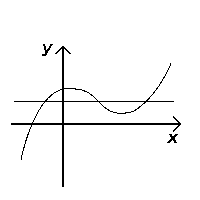A bijection, bijective function, or one-to-one correspondence between two mathematical sets is a function such that each element of the second set is mapped to from exactly one element of the first set. Equivalently, a bijection is a relation between two sets such that each element of either set is paired with exactly one element of the other set.
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is countable if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements.

In mathematics, a diffeomorphism is an isomorphism of smooth manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable.

In mathematics, given two groups, (G,∗) and (H, ·), a group homomorphism from (G,∗) to (H, ·) is a function h : G → H such that for all u and v in G it holds that

In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word isomorphism is derived from the Ancient Greek: ἴσοςisos "equal", and μορφήmorphe "form" or "shape".
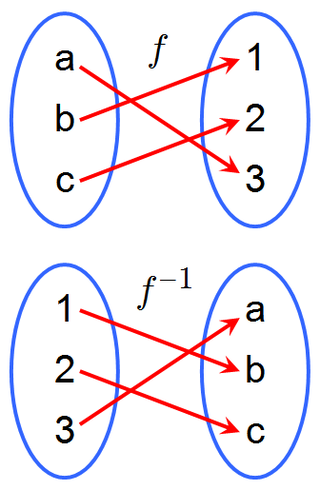
In mathematics, the inverse function of a function f is a function that undoes the operation of f. The inverse of f exists if and only if f is bijective, and if it exists, is denoted by
In mathematics, a partial functionf from a set X to a set Y is a function from a subset S of X to Y. The subset S, that is, the domain of f viewed as a function, is called the domain of definition or natural domain of f. If S equals X, that is, if f is defined on every element in X, then f is said to be a total function.
In mathematics, a surjective function (also known as surjection, or onto function ) is a function f such that, for every element y of the function's codomain, there exists at least one element x in the function's domain such that f(x) = y. In other words, for a function f : X → Y, the codomain Y is the image of the function's domain X. It is not required that x be unique; the function f may map one or more elements of X to the same element of Y.
In mathematics, an injective function (also known as injection, or one-to-one function ) is a function f that maps distinct elements of its domain to distinct elements; that is, x1 ≠ x2 implies f(x1) ≠ f(x2). (Equivalently, f(x1) = f(x2) implies x1 = x2 in the equivalent contrapositive statement.) In other words, every element of the function's codomain is the image of at most one element of its domain. The term one-to-one function must not be confused with one-to-one correspondence that refers to bijective functions, which are functions such that each element in the codomain is an image of exactly one element in the domain.
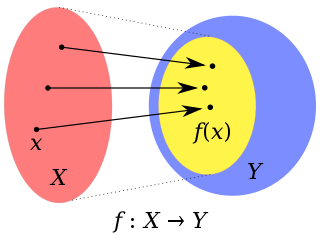
In mathematics, a codomain or set of destination of a function is a set into which all of the output of the function is constrained to fall. It is the set Y in the notation f: X → Y. The term range is sometimes ambiguously used to refer to either the codomain or the image of a function.
In category theory, an epimorphism is a morphism f : X → Y that is right-cancellative in the sense that, for all objects Z and all morphisms g1, g2: Y → Z,
In mathematics, a diffeology on a set generalizes the concept of smooth charts in a differentiable manifold, declaring what the "smooth parametrizations" in the set are.
In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function.

In mathematics, an isometry is a distance-preserving transformation between metric spaces, usually assumed to be bijective. The word isometry is derived from the Ancient Greek: ἴσος isos meaning "equal", and μέτρον metron meaning "measure". If the transformation is from a metric space to itself, it is a kind of geometric transformation known as a motion.
In mathematics, specifically differential calculus, the inverse function theorem gives a sufficient condition for a function to be invertible in a neighborhood of a point in its domain: namely, that its derivative is continuous and non-zero at the point. The theorem also gives a formula for the derivative of the inverse function. In multivariable calculus, this theorem can be generalized to any continuously differentiable, vector-valued function whose Jacobian determinant is nonzero at a point in its domain, giving a formula for the Jacobian matrix of the inverse. There are also versions of the inverse function theorem for complex holomorphic functions, for differentiable maps between manifolds, for differentiable functions between Banach spaces, and so forth.
In mathematics, more specifically in topology, an open map is a function between two topological spaces that maps open sets to open sets. That is, a function is open if for any open set in the image is open in Likewise, a closed map is a function that maps closed sets to closed sets. A map may be open, closed, both, or neither; in particular, an open map need not be closed and vice versa.
In mathematics, differential refers to several related notions derived from the early days of calculus, put on a rigorous footing, such as infinitesimal differences and the derivatives of functions.

In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of the function where the function's derivative is zero. Informally, it is a point where the function "stops" increasing or decreasing.

In mathematics, injections, surjections, and bijections are classes of functions distinguished by the manner in which arguments and images are related or mapped to each other.

In mathematics, a critical point is the argument of a function where the function derivative is zero . The value of the function at a critical point is a critical value.