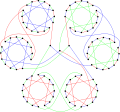
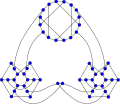
In mathematics, Tait's conjecture states that "Every 3-connected planar cubic graph has a Hamiltonian cycle through all its vertices". It was proposed by P. G. Tait (1884) and disproved by W. T. Tutte (1946), who constructed a counterexample with 25 faces, 69 edges and 46 vertices. Several smaller counterexamples, with 21 faces, 57 edges and 38 vertices, were later proved minimal by Holton & McKay (1988). The condition that the graph be 3-regular is necessary due to polyhedra such as the rhombic dodecahedron, which forms a bipartite graph with six degree-four vertices on one side and eight degree-three vertices on the other side; because any Hamiltonian cycle would have to alternate between the two sides of the bipartition, but they have unequal numbers of vertices, the rhombic dodecahedron is not Hamiltonian.
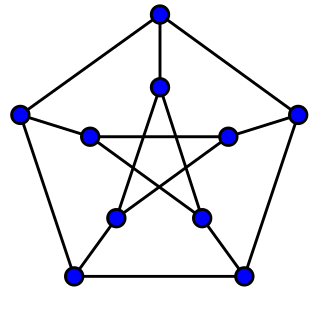
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. Determining whether such paths and cycles exist in graphs are NP-complete.
In graph theory, a uniquely colorable graph is a k-chromatic graph that has only one possible (proper) k-coloring up to permutation of the colors. Equivalently, there is only one way to partition its vertices into k independent sets and there is no way to partition them into k − 1 independent sets.

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.
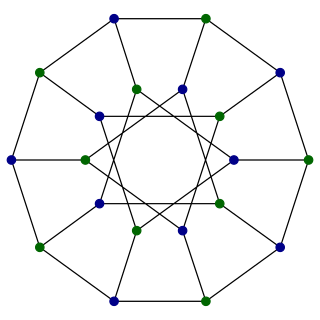
In the mathematical field of graph theory, the Desargues graph is a distance-transitive, cubic graph with 20 vertices and 30 edges. It is named after Girard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial cube, and has been applied in chemical databases.

In graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning k-regular subgraph, and a k-factorization partitions the edges of the graph into disjoint k-factors. A graph G is said to be k-factorable if it admits a k-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a k-regular graph is a proper edge coloring with k colors. A 2-factor is a collection of cycles that spans all vertices of the graph.

In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig (1931), describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.

In graph theory, Grinberg's theorem is a necessary condition for a planar graph to contain a Hamiltonian cycle, based on the lengths of its face cycles. If a graph does not meet this condition, it is not Hamiltonian. The result has been widely used to prove that certain planar graphs constructed to have additional properties are not Hamiltonian; for instance it can prove non-Hamiltonicity of some counterexamples to Tait's conjecture that cubic polyhedral graphs are Hamiltonian.

In the mathematical field of graph theory, the Robertson graph or (4,5)-cage, is a 4-regular undirected graph with 19 vertices and 38 edges named after Neil Robertson.

In the mathematical field of graph theory, the Meredith graph is a 4-regular undirected graph with 70 vertices and 140 edges discovered by Guy H. J. Meredith in 1973.

In the mathematical field of graph theory, the Ellingham–Horton graphs are two 3-regular graphs on 54 and 78 vertices: the Ellingham–Horton 54-graph and the Ellingham–Horton 78-graph. They are named after Joseph D. Horton and Mark N. Ellingham, their discoverers. These two graphs provide counterexamples to the conjecture of W. T. Tutte that every cubic 3-connected bipartite graph is Hamiltonian. The book thickness of the Ellingham-Horton 54-graph and the Ellingham-Horton 78-graph is 3 and the queue numbers 2.

In the mathematical field of graph theory, the Tutte 12-cage or Benson graph is a 3-regular graph with 126 vertices and 189 edges named after W. T. Tutte.
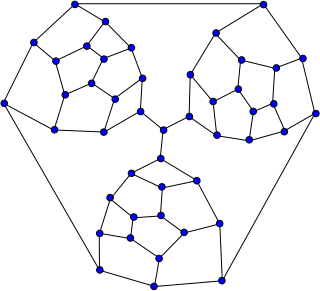
In the mathematical field of graph theory, the Tutte graph is a 3-regular graph with 46 vertices and 69 edges named after W. T. Tutte. It has chromatic number 3, chromatic index 3, girth 4 and diameter 8.

In geometric graph theory, a branch of mathematics, a polyhedral graph is the undirected graph formed from the vertices and edges of a convex polyhedron. Alternatively, in purely graph-theoretic terms, the polyhedral graphs are the 3-vertex-connected, planar graphs.
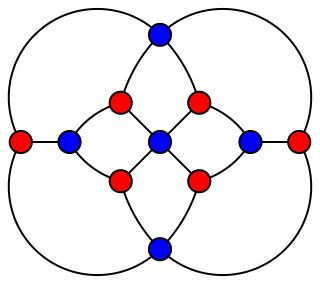
In graph theory, a branch of mathematics, the Herschel graph is a bipartite undirected graph with 11 vertices and 18 edges. It is a polyhedral graph, and is the smallest polyhedral graph that does not have a Hamiltonian cycle, a cycle passing through all its vertices. It is named after British astronomer Alexander Stewart Herschel, because of Herschel's studies of Hamiltonian cycles in polyhedral graphs.
Barnette's conjecture is an unsolved problem in graph theory, a branch of mathematics, concerning Hamiltonian cycles in graphs. It is named after David W. Barnette, a professor emeritus at the University of California, Davis; it states that every bipartite polyhedral graph with three edges per vertex has a Hamiltonian cycle.

In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.

In graph theory, a branch of mathematics, Fleischner's theorem gives a sufficient condition for a graph to contain a Hamiltonian cycle. It states that, if is a 2-vertex-connected graph, then the square of is Hamiltonian. It is named after Herbert Fleischner, who published its proof in 1974.
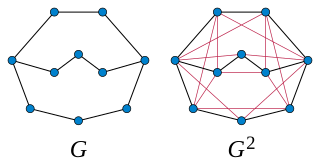
In graph theory, a branch of mathematics, the kth powerGk of an undirected graph G is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in G is at most k. Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: G2 is called the square of G, G3 is called the cube of G, etc.