Hybrid automaton

Last updated December 21, 2024

In automata theory, a hybrid automaton (plural: hybrid automata or hybrid automatons) is a mathematical model for precisely describing hybrid systems, for instance systems in which digital computational processes interact with analog physical processes. A hybrid automaton is a finite-state machine with a finite set of continuous variables whose values are described by a set of ordinary differential equations. This combined specification of discrete and continuous behaviors enables dynamic systems that comprise both digital and analog components to be modeled and analyzed.

Examples

A simple example is a room-thermostat-heater system where the temperature of the room evolves according to laws of thermodynamics and the state of the heater (on/off); the thermostat senses the temperature, performs certain computations and turns the heater on and off. In general, hybrid automata have been used to model and analyze a variety of embedded systems including vehicle control systems, air traffic control systems, mobile robots, and processes from systems biology.

Formal definition

An Alur–Henzinger hybrid automaton $H$ comprises the following components:^[1]

A finite set $X=\{x_{1},...,x_{n}\}$ of real-numbered variables. The number $n$ is called the dimension of $H$ . Let ${\dot {X}}$ be the set $\{{\dot {x}}_{1},...,{\dot {x}}_{n}\}$ of dotted variables that represent first derivatives during continuous change, and let $X'$ be the set $\{x'_{1},...,x'_{n}\}$ of primed variables that represent values at the conclusion of discrete change.
A finite multidigraph $(V,E)$ . The vertices in $V$ are called control modes. The edges in $E$ are called control switches.
Three vertex labeling functions init, inv, and flow that assign to each control mode $v\in V$ three predicates. Each initial condition init $(v)$ is a predicate whose free variables are from $X$ . Each invariant condition inv $(v)$ is a predicate whose free variables are from $X$ . Each flow condition flow $(v)$ is a predicate whose free variables are from $X\cup {\dot {X}}$ .

So this is a labeled multidigraph.

An edge labeling function jump that assigns to each control switch $e\in E$ a predicate. Each jump condition jump $(e)$ is a predicate whose free variables are from $X\cup X'$ .
A finite set $\Sigma$ of events, and an edge labeling function event: $E\rightarrow \Sigma$ that assigns to each control switch an event.

Related models

Hybrid automata come in several flavors: The Alur–Henzinger hybrid automaton is a popular model; it was developed primarily for algorithmic analysis of hybrid systems model checking. The HyTech model checking tool is based on this model. The Hybrid Input/Output Automaton model has been developed more recently. This model enables compositional modeling and analysis of hybrid systems. Another formalism, which is useful to model implementations of hybrid automaton, is the lazy linear hybrid automaton.

Decidable subclass of hybrid automata

Given the expressiveness of hybrid automata it is not surprising that simple reachability questions are undecidable for general hybrid automata. In fact, a straightforward reduction from counter machines to three variables hybrid automata (two variables for storing counter values and one to restrict spending a unit-time per location) proves the undecidability of the reachability problem for hybrid automata. A sub-class of hybrid automata are timed automata ^[2] where all of the variables grow with uniform rate (i.e., all continuous variables have derivative 1). Such restricted variables can act as timer variables, called clocks, and permit modeling of real-time systems. Other notable decidable subclasses include initialized rectangular hybrid automata,^[3] one-dimensional piecewise-constant derivatives (PCD) systems,^[4] priced timed automata,^[5] and constant-rate multi-mode systems.^[6]

Related Research Articles

A finite-state machine (FSM) or finite-state automaton, finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed.

In the theory of computation, a branch of theoretical computer science, a pushdown automaton (PDA) is a type of automaton that employs a stack.

In theoretical computer science and mathematics, the theory of computation is the branch that deals with what problems can be solved on a model of computation, using an algorithm, how efficiently they can be solved or to what degree. The field is divided into three major branches: automata theory and formal languages, computability theory, and computational complexity theory, which are linked by the question: "What are the fundamental capabilities and limitations of computers?".

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a finite automaton (FA) or finite-state machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.

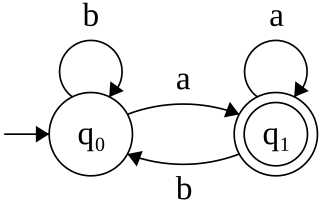
In computer science and automata theory, a deterministic Büchi automaton is a theoretical machine which either accepts or rejects infinite inputs. Such a machine has a set of states and a transition function, which determines which state the machine should move to from its current state when it reads the next input character. Some states are accepting states and one state is the start state. The machine accepts an input if and only if it will pass through an accepting state infinitely many times as it reads the input.

Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science. The computability of a problem is closely linked to the existence of an algorithm to solve the problem.

A hybrid system is a dynamical system that exhibits both continuous and discrete dynamic behavior – a system that can both flow and jump. Often, the term "hybrid dynamical system" is used instead of "hybrid system", to distinguish from other usages of "hybrid system", such as the combination neural nets and fuzzy logic, or of electrical and mechanical drivelines. A hybrid system has the benefit of encompassing a larger class of systems within its structure, allowing for more flexibility in modeling dynamic phenomena.

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.

In automata theory, a deterministic pushdown automaton is a variation of the pushdown automaton. The class of deterministic pushdown automata accepts the deterministic context-free languages, a proper subset of context-free languages.

Language equations are mathematical statements that resemble numerical equations, but the variables assume values of formal languages rather than numbers. Instead of arithmetic operations in numerical equations, the variables are joined by language operations. Among the most common operations on two languages A and B are the set union A ∪ B, the set intersection A ∩ B, and the concatenation A⋅B. Finally, as an operation taking a single operand, the set A^* denotes the Kleene star of the language A. Therefore, language equations can be used to represent formal grammars, since the languages generated by the grammar must be the solution of a system of language equations.

In mathematics, a function or sequence is said to exhibit quadratic growth when its values are proportional to the square of the function argument or sequence position. "Quadratic growth" often means more generally "quadratic growth in the limit", as the argument or sequence position goes to infinity – in big Theta notation, $. This can be defined both continuously or discretely.$

Rajeev Alur is an American professor of computer science at the University of Pennsylvania who has made contributions to formal methods, programming languages, and automata theory, including notably the introduction of timed automata and nested words.

In mathematical logic, monadic second-order logic (MSO) is the fragment of second-order logic where the second-order quantification is limited to quantification over sets. It is particularly important in the logic of graphs, because of Courcelle's theorem, which provides algorithms for evaluating monadic second-order formulas over graphs of bounded treewidth. It is also of fundamental importance in automata theory, where the Büchi–Elgot–Trakhtenbrot theorem gives a logical characterization of the regular languages.

In computer science, more specifically in automata and formal language theory, nested words are a concept proposed by Alur and Madhusudan as a joint generalization of words, as traditionally used for modelling linearly ordered structures, and of ordered unranked trees, as traditionally used for modelling hierarchical structures. Finite-state acceptors for nested words, so-called nested word automata, then give a more expressive generalization of finite automata on words. The linear encodings of languages accepted by finite nested word automata gives the class of visibly pushdown languages. The latter language class lies properly between the regular languages and the deterministic context-free languages. Since their introduction in 2004, these concepts have triggered much research in that area.

In automata theory, a timed automaton is a finite automaton extended with a finite set of real-valued clocks. During a run of a timed automaton, clock values increase all with the same speed. Along the transitions of the automaton, clock values can be compared to integers. These comparisons form guards that may enable or disable transitions and by doing so constrain the possible behaviors of the automaton. Further, clocks can be reset. Timed automata are a sub-class of a type hybrid automata.

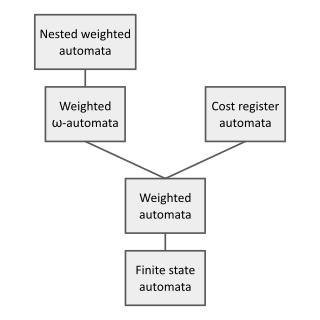
In theoretical computer science and formal language theory, a weighted automaton or weighted finite-state machine is a generalization of a finite-state machine in which the edges have weights, for example real numbers or integers. Finite-state machines are only capable of answering decision problems; they take as input a string and produce a Boolean output, i.e. either "accept" or "reject". In contrast, weighted automata produce a quantitative output, for example a count of how many answers are possible on a given input string, or a probability of how likely the input string is according to a probability distribution. They are one of the simplest studied models of quantitative automata.

In model checking, a subfield of computer science, a signal or timed state sequence is an extension of the notion of words in a formal language, in which letters are continuously emitted. While a word is traditionally defined as a function from a set of non-negative integers to letters, a signal is a function from a set of real numbers to letters. This allow the use of formalisms similar to the ones of automata theory to deal with continuous signals.

In model checking, a subfield of computer science, a clock is a mathematical object used to model time. More precisely, a clock measures how much time passed since a particular event occurs, in this sense, a clock is more precisely an abstraction of a stopwatch. In a model of some particular program, the value of the clock may either be the time since the program was started, or the time since a particular event occurred in the program. Those clocks are used in the definition of timed automaton, signal automaton, timed propositional temporal logic and clock temporal logic. They are also used in programs such as UPPAAL which implement timed automata.

An alternating timed automaton (ATA) is a modeling formalism that combines features of timed automaton and an alternating finite automaton to succinctly express sets of timed event sequences. Classical timed automata only allow existential nondeterministic branching in their transitions, while alternating finite automata model discrete untimed behaviors. Unlike timed automata, alternating timed automata are closed under complementation. However, this increased expressive power comes at the cost of undecidability in their emptiness problem. A one clock alternating timed automaton (OCATA) is a restricted version of an ATA, limited to the use of a single clock. OCATAs can express timed languages that cannot be expressed using standard timed automata.

In mathematics, S2S is the monadic second order theory with two successors. It is one of the most expressive natural decidable theories known, with many decidable theories interpretable in S2S. Its decidability was proved by Rabin in 1969.

References

↑ Henzinger, T.A. "The Theory of Hybrid Automata". Proceedings of the Eleventh Annual IEEE Symposium on Logic in Computer Science (LICS), pages 278-292, 1996.
↑ Alur, R. and Dill, D. L. "A Theory of Timed Automata". Theoretical Computer Science (TCS), 126(2), pages 183-235, 1995.
↑ Henzinger, Thomas A.; Kopke, Peter W.; Puri, Anuj; Varaiya, Pravin (1998-08-01). "What's Decidable about Hybrid Automata?". Journal of Computer and System Sciences. 57 (1): 94–124. doi:10.1006/jcss.1998.1581. hdl: 1813/7198 . ISSN 0022-0000.
↑ Asarin, Eugene; Schneider, Gerardo; Yovine, Sergio (2001), "On the Decidability of the Reachability Problem for Planar Differential Inclusions", Hybrid Systems: Computation and Control, Springer Berlin Heidelberg, pp. 89–104, CiteSeerX 10.1.1.23.8172 , doi:10.1007/3-540-45351-2_11, ISBN 9783540418665
↑ Behrmann, Gerd; Larsen, Kim G.; Rasmussen, Jacob I. (2005), "Priced Timed Automata: Algorithms and Applications", Formal Methods for Components and Objects, Springer Berlin Heidelberg, pp. 162–182, CiteSeerX 10.1.1.106.7115 , doi:10.1007/11561163_8, ISBN 9783540291312
↑ Alur, Rajeev; Trivedi, Ashutosh; Wojtczak, Dominik (2012-04-17). Optimal scheduling for constant-rate multi-mode systems. ACM. pp. 75–84. CiteSeerX 10.1.1.299.946 . doi:10.1145/2185632.2185647. ISBN 9781450312202. S2CID 14587340.