
In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices.
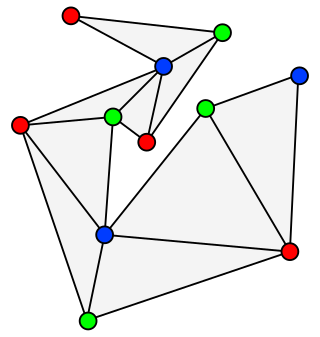
In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.
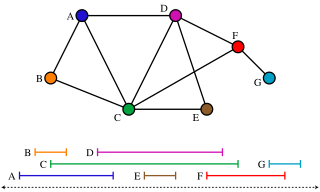
In graph theory, an interval graph is an undirected graph formed from a set of intervals on the real line, with a vertex for each interval and an edge between vertices whose intervals intersect. It is the intersection graph of the intervals.

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.
In constraint satisfaction, a decomposition method translates a constraint satisfaction problem into another constraint satisfaction problem that is binary and acyclic. Decomposition methods work by grouping variables into sets, and solving a subproblem for each set. These translations are done because solving binary acyclic problems is a tractable problem.
In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order. Comparability graphs have also been called transitively orientable graphs, partially orderable graphs, containment graphs, and divisor graphs. An incomparability graph is an undirected graph that connects pairs of elements that are not comparable to each other in a partial order.
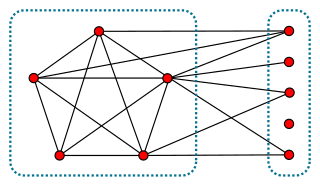
In graph theory, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique and an independent set. Split graphs were first studied by Földes and Hammer, and independently introduced by Tyshkevich and Chernyak (1979).
In graph theory, particularly in the theory of hypergraphs, the line graph of a hypergraphH, denoted L(H), is the graph whose vertex set is the set of the hyperedges of H, with two vertices adjacent in L(H) when their corresponding hyperedges have a nonempty intersection in H. In other words, L(H) is the intersection graph of a family of finite sets. It is a generalization of the line graph of a graph.

In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

In the mathematical field of graph theory, a permutation graph is a graph whose vertices represent the elements of a permutation, and whose edges represent pairs of elements that are reversed by the permutation. Permutation graphs may also be defined geometrically, as the intersection graphs of line segments whose endpoints lie on two parallel lines. Different permutations may give rise to the same permutation graph; a given graph has a unique representation if it is prime with respect to the modular decomposition.
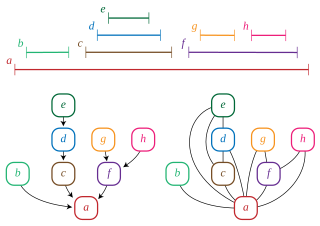
In graph theory, a trivially perfect graph is a graph with the property that in each of its induced subgraphs the size of the maximum independent set equals the number of maximal cliques. Trivially perfect graphs were first studied by but were named by Golumbic (1978); Golumbic writes that "the name was chosen since it is trivial to show that such a graph is perfect." Trivially perfect graphs are also known as comparability graphs of trees, arborescent comparability graphs, and quasi-threshold graphs.
In graph theory, a perfectly orderable graph is a graph whose vertices can be ordered in such a way that a greedy coloring algorithm with that ordering optimally colors every induced subgraph of the given graph. Perfectly orderable graphs form a special case of the perfect graphs, and they include the chordal graphs, comparability graphs, and distance-hereditary graphs. However, testing whether a graph is perfectly orderable is NP-complete.
In the mathematical area of graph theory, an undirected graph G is strongly chordal if it is a chordal graph and every cycle of even length in G has an odd chord, i.e., an edge that connects two vertices that are an odd distance (>1) apart from each other in the cycle.
In the mathematical area of graph theory, a chordal bipartite graph is a bipartite graph B = (X,Y,E) in which every cycle of length at least 6 in B has a chord, i.e., an edge that connects two vertices that are a distance > 1 apart from each other in the cycle. A better name would be weakly chordal and bipartite since chordal bipartite graphs are in general not chordal as the induced cycle of length 4 shows.
Andreas Brandstädt is a German mathematician and computer scientist.
In the mathematical area of graph theory, an undirected graph G is dually chordal if the hypergraph of its maximal cliques is a hypertree. The name comes from the fact that a graph is chordal if and only if the hypergraph of its maximal cliques is the dual of a hypertree. Originally, these graphs were defined by maximum neighborhood orderings and have a variety of different characterizations. Unlike for chordal graphs, the property of being dually chordal is not hereditary, i.e., induced subgraphs of a dually chordal graph are not necessarily dually chordal, and a dually chordal graph is in general not a perfect graph.

In the mathematical area of graph theory, a k-leaf power of a tree T is a graph G whose vertices are the leaves of T and whose edges connect pairs of leaves whose distance in T is at most k. That is, G is an induced subgraph of the graph power , induced by the leaves of T. For a graph G constructed in this way, T is called a k-leaf root of G.
In graph theory, a matching in a hypergraph is a set of hyperedges, in which every two hyperedges are disjoint. It is an extension of the notion of matching in a graph.
In graph theory, a balanced hypergraph is a hypergraph that has several properties analogous to that of a bipartite graph.










