Line graph of a hypergraph

Last updated

In graph theory, particularly in the theory of hypergraphs, the line graph of a hypergraphH, denoted L(H), is the graph whose vertex set is the set of the hyperedges of H, with two vertices adjacent in L(H) when their corresponding hyperedges have a nonempty intersection in H. In other words, L(H) is the intersection graph of a family of finite sets. It is a generalization of the line graph of a graph.

Contents

Questions about line graphs of hypergraphs are often generalizations of questions about line graphs of graphs. For instance, a hypergraph whose edges all have size k is called k-uniform. (A 2-uniform hypergraph is a graph). In hypergraph theory, it is often natural to require that hypergraphs be k-uniform. Every graph is the line graph of some hypergraph, but, given a fixed edge size k, not every graph is a line graph of some k-uniform hypergraph. A main problem is to characterize those that are, for each k ≥ 3.

A hypergraph is linear if each pair of hyperedges intersects in at most one vertex. Every graph is the line graph, not only of some hypergraph, but of some linear hypergraph. [1]

Line graphs of k-uniform hypergraphs, k ≥ 3

Beineke [2] characterized line graphs of graphs by a list of 9 forbidden induced subgraphs. (See the article on line graphs.) No characterization by forbidden induced subgraphs is known of line graphs of k-uniform hypergraphs for any k ≥ 3, and Lovász [3] showed there is no such characterization by a finite list if k = 3.

Krausz [4] characterized line graphs of graphs in terms of clique covers. (See Line Graphs.) A global characterization of Krausz type for the line graphs of k-uniform hypergraphs for any k ≥ 3 was given by Berge [5]

Line graphs of k-uniform linear hypergraphs, k ≥ 3

A global characterization of Krausz type for the line graphs of k-uniform linear hypergraphs for any k ≥ 3 was given by Naik, Rao, Shrikhande, and Singhi. [6] At the same time, they found a finite list of forbidden induced subgraphs for linear 3-uniform hypergraphs with minimum vertex degree at least 69. Metelsky|l and Tyshkevich [7] and Jacobson, Kézdy, and Lehel [8] improved this bound to 19. At last Skums, Suzdal', and Tyshkevich [9] reduced this bound to 16. Metelsky and Tyshkevich [10] also proved that, if k > 3, no such finite list exists for linear k-uniform hypergraphs, no matter what lower bound is placed on the degree.

The difficulty in finding a characterization of linear k-uniform hypergraphs is due to the fact that there are infinitely many forbidden induced subgraphs. To give examples, for m > 0, consider a chain of m diamond graphs such that the consecutive diamonds share vertices of degree two. For k ≥ 3, add pendant edges at every vertex of degree 2 or 4 to get one of the families of minimal forbidden subgraphs of Naik, Rao, Shrikhande, and Singhi [11] as shown here. This does not rule out either the existence of a polynomial recognition or the possibility of a forbidden induced subgraph characterization similar to Beineke's of line graphs of graphs.

Repeated diamond graph.svg

There are some interesting characterizations available for line graphs of linear k-uniform hypergraphs due to various authors [12] under constraints on the minimum degree or the minimum edge degree of G. Minimum edge degree at least k3-2k2+1 in Naik, Rao, Shrikhande, and Singhi [13] is reduced to 2k2-3k+1 in Jacobson, Kézdy, and Lehel [14] and Zverovich [15] to characterize line graphs of k-uniform linear hypergraphs for any k ≥ 3.

The complexity of recognizing line graphs of linear k-uniform hypergraphs without any constraint on minimum degree (or minimum edge-degree) is not known. For k = 3 and minimum degree at least 19, recognition is possible in polynomial time. [16] Skums, Suzdal', and Tyshkevich [17] reduced the minimum degree to 10.

There are many interesting open problems and conjectures in Naik et al., Jacoboson et al., Metelsky et al. and Zverovich.

Disjointness graph

The disjointness graph of a hypergraph H, denoted D(H), is the graph whose vertex set is the set of the hyperedges of H, with two vertices adjacent in D(H) when their corresponding hyperedges are disjoint in H. [18] In other words, D(H) is the complement graph of L(H). A clique in D(H) corresponds to an independent set in L(H), and vice versa.

Related Research Articles

<span class="mw-page-title-main">Hypergraph</span> Generalization of graph theory

In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices.

<span class="mw-page-title-main">Bipartite graph</span> Graph divided into two independent sets

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.

<span class="mw-page-title-main">Extremal graph theory</span>

Extremal graph theory is a branch of combinatorics, itself an area of mathematics, that lies at the intersection of extremal combinatorics and graph theory. In essence, extremal graph theory studies how global properties of a graph influence local substructure. Results in extremal graph theory deal with quantitative connections between various graph properties, both global and local, and problems in extremal graph theory can often be formulated as optimization problems: how big or small a parameter of a graph can be, given some constraints that the graph has to satisfy? A graph that is an optimal solution to such an optimization problem is called an extremal graph, and extremal graphs are important objects of study in extremal graph theory.

<span class="mw-page-title-main">Perfect graph</span> Graph with tight clique-coloring relation

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

In the mathematical discipline of graph theory, the line graph of an undirected graph G is another graph L(G) that represents the adjacencies between edges of G. L(G) is constructed in the following way: for each edge in G, make a vertex in L(G); for every two edges in G that have a vertex in common, make an edge between their corresponding vertices in L(G).

<span class="mw-page-title-main">Erdős–Faber–Lovász conjecture</span>

In graph theory, the Erdős–Faber–Lovász conjecture is a problem about graph coloring, named after Paul Erdős, Vance Faber, and László Lovász, who formulated it in 1972. It says:

<span class="mw-page-title-main">Rook's graph</span> Graph of chess rook moves

In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and there is an edge between any two squares sharing a row (rank) or column (file), the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape. Although rook's graphs have only minor significance in chess lore, they are more important in the abstract mathematics of graphs through their alternative constructions: rook's graphs are the Cartesian product of two complete graphs, and are the line graphs of complete bipartite graphs. The square rook's graphs constitute the two-dimensional Hamming graphs.

In graph theory, a branch of mathematics, many important families of graphs can be described by a finite set of individual graphs that do not belong to the family and further exclude all graphs from the family which contain any of these forbidden graphs as (induced) subgraph or minor.

<span class="mw-page-title-main">Distance-hereditary graph</span> Graph whose induced subgraphs preserve distance

In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

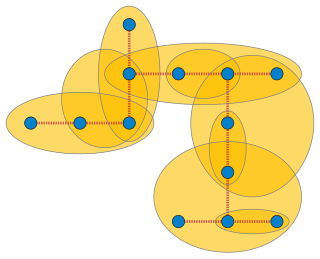
<span class="mw-page-title-main">Hypertree</span> Generalization of tree graphs to hypergraphs

In the mathematical field of graph theory, a hypergraph H is called a hypertree if it admits a host graph T such that T is a tree. In other words, H is a hypertree if there exists a tree T such that every hyperedge of H is the set of vertices of a connected subtree of T. Hypertrees have also been called arboreal hypergraphs or tree hypergraphs.

In the mathematical discipline of graph theory, a rainbow matching in an edge-colored graph is a matching in which all the edges have distinct colors.

In the theory of permutation patterns, a skew-merged permutation is a permutation that can be partitioned into an increasing sequence and a decreasing sequence. They were first studied by Stankova (1994) and given their name by Atkinson (1998).

<span class="mw-page-title-main">Locally linear graph</span> Graph where every edge is in one triangle

In graph theory, a locally linear graph is an undirected graph in which every edge belongs to exactly one triangle. Equivalently, for each vertex of the graph, its neighbors are each adjacent to exactly one other neighbor, so the neighbors can be paired up into an induced matching. Locally linear graphs have also been called locally matched graphs. Their triangles form the hyperedges of triangle-free 3-uniform linear hypergraphs and the blocks of certain partial Steiner triple systems, and the locally linear graphs are exactly the Gaifman graphs of these hypergraphs or partial Steiner systems.

In graph theory, the hypergraph removal lemma states that when a hypergraph contains few copies of a given sub-hypergraph, then all of the copies can be eliminated by removing a small number of hyperedges. It is a generalization of the graph removal lemma. The special case in which the graph is a tetrahedron is known as the tetrahedron removal lemma. It was first proved by Nagle, Rödl, Schacht and Skokan and, independently, by Gowers.

In graph theory, a matching in a hypergraph is a set of hyperedges, in which every two hyperedges are disjoint. It is an extension of the notion of matching in a graph.

In graph theory, a vertex cover in a hypergraph is a set of vertices, such that every hyperedge of the hypergraph contains at least one vertex of that set. It is an extension of the notion of vertex cover in a graph.

In the mathematical field of graph theory, Hall-type theorems for hypergraphs are several generalizations of Hall's marriage theorem from graphs to hypergraphs. Such theorems were proved by Ofra Kessler, Ron Aharoni, Penny Haxell, Roy Meshulam, and others.

In graph theory, a balanced hypergraph is a hypergraph that has several properties analogous to that of a bipartite graph.

In graph theory, Ryser's conjecture is a conjecture relating the maximum matching size and the minimum transversal size in hypergraphs.

A sparsity matroid is a mathematical structure that captures how densely a multigraph is populated with edges. To unpack this a little, sparsity is a measure of density of a graph that bounds the number of edges in any subgraph. The property of having a particular matroid as its density measure is invariant under graph isomorphisms and so it is a graph invariant.

References

  1. ↑ ( Berge 1989 )
  2. ↑ Beineke (1968)
  3. ↑ Lovász (1977)
  4. ↑ Krausz (1943)
  5. ↑ Berge (1989)
  6. ↑ Naik et al. (1980)
  7. ↑ Metelsky & Tyshkevich (1997)
  8. ↑ Jacobson, Kézdy & Lehel (1997)
  9. ↑ Skums, Suzdal' & Tyshkevich (2009)
  10. ↑ Metelsky & Tyshkevich (1997)
  11. ↑ Naik et al. (1980), Naik et al. (1982)
  12. ↑ Naik et al. (1980), Naik et al. (1982), Jacobson, Kézdy & Lehel 1997, Metelsky & Tyshkevich 1997, and Zverovich 2004
  13. ↑ Naik et al. (1980)
  14. ↑ Jacobson, Kézdy & Lehel (1997)
  15. ↑ Zverovich (2004)
  16. ↑ Jacobson, Kézdy & Lehel 1997 and Metelsky & Tyshkevich 1997
  17. ↑ Skums, Suzdal' & Tyshkevich (2009)
  18. ↑ Meshulam, Roy (2001-01-01). "The Clique Complex and Hypergraph Matching". Combinatorica. 21 (1): 89–94. doi:10.1007/s004930170006. ISSN   1439-6912. S2CID   207006642.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.