In a chemical reaction, chemical equilibrium is the state in which both the reactants and products are present in concentrations which have no further tendency to change with time, so that there is no observable change in the properties of the system. This state results when the forward reaction proceeds at the same rate as the reverse reaction. The reaction rates of the forward and backward reactions are generally not zero, but they are equal. Thus, there are no net changes in the concentrations of the reactants and products. Such a state is known as dynamic equilibrium.
Raoult's law ( law) is a relation of physical chemistry, with implications in thermodynamics. Proposed by French chemist François-Marie Raoult in 1887, it states that the partial pressure of each component of an ideal mixture of liquids is equal to the vapor pressure of the pure component multiplied by its mole fraction in the mixture. In consequence, the relative lowering of vapor pressure of a dilute solution of nonvolatile solute is equal to the mole fraction of solute in the solution.
In electrochemistry, the Nernst equation is a chemical thermodynamical relationship that permits the calculation of the reduction potential of a reaction from the standard electrode potential, absolute temperature, the number of electrons involved in the oxydo-reduction reaction, and activities of the chemical species undergoing reduction and oxidation respectively. It was named after Walther Nernst, a German physical chemist who formulated the equation.
In chemical thermodynamics, activity is a measure of the "effective concentration" of a species in a mixture, in the sense that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution. The term "activity" in this sense was coined by the American chemist Gilbert N. Lewis in 1907.

In optics, a Fabry–Pérot interferometer (FPI) or etalon is an optical cavity made from two parallel reflecting surfaces. Optical waves can pass through the optical cavity only when they are in resonance with it. It is named after Charles Fabry and Alfred Perot, who developed the instrument in 1899. Etalon is from the French étalon, meaning "measuring gauge" or "standard".
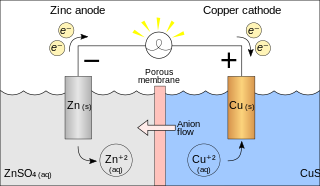
A galvanic cell or voltaic cell, named after the scientists Luigi Galvani and Alessandro Volta, respectively, is an electrochemical cell in which an electric current is generated from spontaneous Oxidation-Reduction reactions. A common apparatus generally consists of two different metals, each immersed in separate beakers containing their respective metal ions in solution that are connected by a salt bridge or separated by a porous membrane.
In physics, chemistry and biology, a potential gradient is the local rate of change of the potential with respect to displacement, i.e. spatial derivative, or gradient. This quantity frequently occurs in equations of physical processes because it leads to some form of flux.

The classical rocket equation, or ideal rocket equation is a mathematical equation that describes the motion of vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself using thrust by expelling part of its mass with high velocity can thereby move due to the conservation of momentum. It is credited to the Russian scientist Konstantin Tsiolkovsky who independently derived it and published it in 1903, although it had been independently derived and published by the British mathematician William Moore in 1810, and later published in a separate book in 1813. American Robert Goddard also developed it independently in 1912, and German Hermann Oberth derived it independently about 1920.
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency towards further change. For a given set of reaction conditions, the equilibrium constant is independent of the initial analytical concentrations of the reactant and product species in the mixture. Thus, given the initial composition of a system, known equilibrium constant values can be used to determine the composition of the system at equilibrium. However, reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant.

In quantum field theory, the quantum effective action is a modified expression for the classical action taking into account quantum corrections while ensuring that the principle of least action applies, meaning that extremizing the effective action yields the equations of motion for the vacuum expectation values of the quantum fields. The effective action also acts as a generating functional for one-particle irreducible correlation functions. The potential component of the effective action is called the effective potential, with the expectation value of the true vacuum being the minimum of this potential rather than the classical potential, making it important for studying spontaneous symmetry breaking.
An activity coefficient is a factor used in thermodynamics to account for deviations from ideal behaviour in a mixture of chemical substances. In an ideal mixture, the microscopic interactions between each pair of chemical species are the same and, as a result, properties of the mixtures can be expressed directly in terms of simple concentrations or partial pressures of the substances present e.g. Raoult's law. Deviations from ideality are accommodated by modifying the concentration by an activity coefficient. Analogously, expressions involving gases can be adjusted for non-ideality by scaling partial pressures by a fugacity coefficient.

The chemists Peter Debye and Erich Hückel noticed that solutions that contain ionic solutes do not behave ideally even at very low concentrations. So, while the concentration of the solutes is fundamental to the calculation of the dynamics of a solution, they theorized that an extra factor that they termed gamma is necessary to the calculation of the activity coefficients of the solution. Hence they developed the Debye–Hückel equation and Debye–Hückel limiting law. The activity is only proportional to the concentration and is altered by a factor known as the activity coefficient . This factor takes into account the interaction energy of ions in solution.

In electrochemistry, and more generally in solution chemistry, a Pourbaix diagram, also known as a potential/pH diagram, EH–pH diagram or a pE/pH diagram, is a plot of possible thermodynamically stable phases of an aqueous electrochemical system. Boundaries (50 %/50 %) between the predominant chemical species are represented by lines. As such a Pourbaix diagram can be read much like a standard phase diagram with a different set of axes. Similarly to phase diagrams, they do not allow for reaction rate or kinetic effects. Beside potential and pH, the equilibrium concentrations are also dependent upon, e.g., temperature, pressure, and concentration. Pourbaix diagrams are commonly given at room temperature, atmospheric pressure, and molar concentrations of 10−6 and changing any of these parameters will yield a different diagram.
The Gibbs adsorption isotherm for multicomponent systems is an equation used to relate the changes in concentration of a component in contact with a surface with changes in the surface tension, which results in a corresponding change in surface energy. For a binary system, the Gibbs adsorption equation in terms of surface excess is:
Absolute electrode potential, in electrochemistry, according to an IUPAC definition, is the electrode potential of a metal measured with respect to a universal reference system.
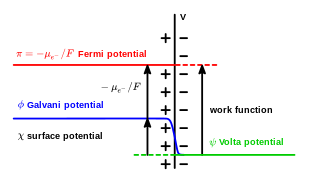
In electrochemistry, the Galvani potential is the electric potential difference between two points in the bulk of two phases. These phases can be two different solids, or a solid and a liquid.
In electrochemistry, the Butler–Volmer equation, also known as Erdey-Grúz–Volmer equation, is one of the most fundamental relationships in electrochemical kinetics. It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction, considering that both a cathodic and an anodic reaction occur on the same electrode:
An osmotic coefficient is a quantity which characterises the deviation of a solvent from ideal behaviour, referenced to Raoult's law. It can be also applied to solutes. Its definition depends on the ways of expressing chemical composition of mixtures.
Pitzer equations are important for the understanding of the behaviour of ions dissolved in natural waters such as rivers, lakes and sea-water. They were first described by physical chemist Kenneth Pitzer. The parameters of the Pitzer equations are linear combinations of parameters, of a virial expansion of the excess Gibbs free energy, which characterise interactions amongst ions and solvent. The derivation is thermodynamically rigorous at a given level of expansion. The parameters may be derived from various experimental data such as the osmotic coefficient, mixed ion activity coefficients, and salt solubility. They can be used to calculate mixed ion activity coefficients and water activities in solutions of high ionic strength for which the Debye–Hückel theory is no longer adequate. They are more rigorous than the equations of specific ion interaction theory, but Pitzer parameters are more difficult to determine experimentally than SIT parameters.
Equilibrium chemistry is concerned with systems in chemical equilibrium. The unifying principle is that the free energy of a system at equilibrium is the minimum possible, so that the slope of the free energy with respect to the reaction coordinate is zero. This principle, applied to mixtures at equilibrium provides a definition of an equilibrium constant. Applications include acid–base, host–guest, metal–complex, solubility, partition, chromatography and redox equilibria.
















