In mathematics, specifically category theory, a functor is a map between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.
In category theory, a branch of mathematics, when we say that a construction satisfies a universal property, it means that this construction can be seen as an initial or terminal object of some other category. By "universal property" one may mean either a universal initial or terminal morphism. The nomination of initial/terminal morphisms comes from the fact that these two morphisms are respectively initial/terminal objects in their corresponding comma categories which has been made from the original ones. Intuitively, by universal we mean that the initial/terminal morphism(s) is (are) the "most general" constructions in that category with those properties.
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed, this intuition can be formalized to define so-called functor categories. Natural transformations are, after categories and functors, one of the most fundamental notions of category theory and consequently appear in the majority of its applications.
In mathematics, specifically category theory, adjunction is a relationship that two functors may have. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
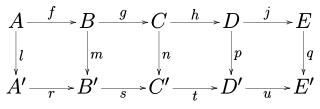
In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. Commutative diagrams play the role in category theory that equations play in algebra.
In category theory, a branch of mathematics, an enriched category generalizes the idea of a category by replacing hom-sets with objects from a general monoidal category. It is motivated by the observation that, in many practical applications, the hom-set often has additional structure that should be respected, e.g., that of being a vector space of morphisms, or a topological space of morphisms. In an enriched category, the set of morphisms associated with every pair of objects is replaced by an object in some fixed monoidal category of "hom-objects". In order to emulate the (associative) composition of morphisms in an ordinary category, the hom-category must have a means of composing hom-objects in an associative manner: that is, there must be a binary operation on objects giving us at least the structure of a monoidal category, though in some contexts the operation may also need to be commutative and perhaps also to have a right adjoint.
In category theory, a category is considered Cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in that their internal language is the simply typed lambda calculus. They are generalized by closed monoidal categories, whose internal language, linear type systems, are suitable for both quantum and classical computation.
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of smaller open sets covering the original one. For example, such data can consist of the rings of continuous or smooth real-valued functions defined on each open set. Sheaves are by design quite general and abstract objects, and their correct definition is rather technical. They are variously defined, for example, as sheaves of sets or sheaves of rings, depending on the type of data assigned to open sets.
In category theory, a branch of mathematics, duality is a correspondence between the properties of a category C and the dual properties of the opposite category Cop. Given a statement regarding the category C, by interchanging the source and target of each morphism as well as interchanging the order of composing two morphisms, a corresponding dual statement is obtained regarding the opposite category Cop. Duality, as such, is the assertion that truth is invariant under this operation on statements. In other words, if a statement is true about C, then its dual statement is true about Cop. Also, if a statement is false about C, then its dual has to be false about Cop.
In category theory, a branch of mathematics, a monad is an endofunctor, together with two natural transformations required to fulfill certain coherence conditions. Monads are used in the theory of pairs of adjoint functors, and they generalize closure operators on partially ordered sets to arbitrary categories.
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object.
In mathematics, particularly category theory, a representable functor is a certain functor from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures allowing one to utilize, as much as possible, knowledge about the category of sets in other settings.
Fibred categories are abstract entities in mathematics used to provide a general framework for descent theory. They formalise the various situations in geometry and algebra in which inverse images of objects such as vector bundles can be defined. As an example, for each topological space there is the category of vector bundles on the space, and for every continuous map from a topological space X to another topological space Y is associated the pullback functor taking bundles on Y to bundles on X. Fibred categories formalise the system consisting of these categories and inverse image functors. Similar setups appear in various guises in mathematics, in particular in algebraic geometry, which is the context in which fibred categories originally appeared. Fibered categories are used to define stacks, which are fibered categories with "descent". Fibrations also play an important role in categorical semantics of type theory, and in particular that of dependent type theories.
In mathematics, specifically in category theory, an exponential object or map object is the categorical generalization of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories. Categories without adjoined products may still have an exponential law.
This is a glossary of properties and concepts in category theory in mathematics.
In category theory, a Kleisli category is a category naturally associated to any monad T. It is equivalent to the category of free T-algebras. The Kleisli category is one of two extremal solutions to the question Does every monad arise from an adjunction? The other extremal solution is the Eilenberg–Moore category. Kleisli categories are named for the mathematician Heinrich Kleisli.
In mathematics, a topos is a category that behaves like the category of sheaves of sets on a topological space. Topoi behave much like the category of sets and possess a notion of localization; they are a direct generalization of point-set topology. The Grothendieck topoi find applications in algebraic geometry; the more general elementary topoi are used in logic.
In mathematics, Grothendieck's six operations, named after Alexander Grothendieck, is a formalism in homological algebra. It originally sprang from the relations in étale cohomology that arise from a morphism of schemes f : X → Y. The basic insight was that many of the elementary facts relating cohomology on X and Y were formal consequences of a small number of axioms. These axioms hold in many cases completely unrelated to the original context, and therefore the formal consequences also hold. The six operations formalism has since been shown to apply to contexts such as D-modules on algebraic varieties, sheaves on locally compact topological spaces, and motives.



