Inverted Dirichlet distribution

Last updated January 27, 2024

In statistics, the inverted Dirichlet distribution is a multivariate generalization of the beta prime distribution, and is related to the Dirichlet distribution. It was first described by Tiao and Cuttman in 1965.^[1]

The distribution has a density function given by

p\left(x_{1},\ldots ,x_{k}\right)={\frac {\Gamma \left(\nu _{1}+\cdots +\nu _{k+1}\right)}{\prod _{j=1}^{k+1}\Gamma \left(\nu _{j}\right)}}x_{1}^{\nu _{1}-1}\cdots x_{k}^{\nu _{k}-1}\times \left(1+\sum _{i=1}^{k}x_{i}\right)^{-\sum _{j=1}^{k+1}\nu _{j}},\qquad x_{i}>0.

The distribution has applications in statistical regression and arises naturally when considering the multivariate Student distribution. It can be characterized^[2] by its mixed moments:

E\left[\prod _{i=1}^{k}x_{i}^{q_{i}}\right]={\frac {\Gamma \left(\nu _{k+1}-\sum _{j=1}^{k}q_{j}\right)}{\Gamma \left(\nu _{k+1}\right)}}\prod _{j=1}^{k}{\frac {\Gamma \left(\nu _{j}+q_{j}\right)}{\Gamma \left(\nu _{j}\right)}}

provided that $q_{j}>-\nu _{j},1\leqslant j\leqslant k$ and $\nu _{k+1}>q_{1}+\ldots +q_{k}$ .

The inverted Dirichlet distribution is conjugate to the negative multinomial distribution if a generalized form of odds ratio is used instead of the categories' probabilities- if the negative multinomial parameter vector is given by $p$ , by changing parameters of the negative multinomial to $x_{i}={\frac {p_{i}}{p_{0}}},i=1\ldots k$ where $p_{0}=1-\sum _{i=1}^{k}p_{i}$ .

T. Bdiri et al. have developed several models that use the inverted Dirichlet distribution to represent and model non-Gaussian data. They have introduced finite ^[3]^[4] and infinite ^[5] mixture models of inverted Dirichlet distributions using the Newton–Raphson technique to estimate the parameters and the Dirichlet process to model infinite mixtures. T. Bdiri et al. have also used the inverted Dirichlet distribution to propose an approach to generate Support Vector Machine kernels ^[6] basing on Bayesian inference and another approach to establish hierarchical clustering.^[7]^[8]

Related Research Articles

In probability and statistics, Student's $t$ distribution $is a continuous probability distribution that generalizes the standard normal distribution. Like the latter, it is symmetric around zero and bell-shaped.$

In probability theory and statistics, the chi-squared distribution with $degrees of freedom is the distribution of a sum of the squares of independent standard normal random variables. The chi-squared distribution is a special case of the gamma distribution and is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in construction of confidence intervals. This distribution is sometimes called the central chi-squared distribution, a special case of the more general noncentral chi-squared distribution.$

In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It models a broad range of random variables, largely in the nature of a time to failure or time between events. Examples are maximum one-day rainfalls and the time a user spends on a web page.

In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:

With a shape parameter $and a scale parameter .$
With a shape parameter $and an inverse scale parameter, called a rate parameter.$

In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, including the enabling of the user to calculate expectations, covariances using differentiation based on some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural sets of distributions to consider. The term exponential class is sometimes used in place of "exponential family", or the older term Koopman–Darmois family. Sometimes loosely referred to as "the" exponential family, this class of distributions is distinct because they all possess a variety of desirable properties, most importantly the existence of a sufficient statistic.

<span class="mw-page-title-main">Dirichlet distribution</span> Probability distribution

In probability and statistics, the Dirichlet distribution (after Peter Gustav Lejeune Dirichlet), often denoted $, is a family of continuous multivariate probability distributions parameterized by a vector of positive reals. It is a multivariate generalization of the beta distribution, hence its alternative name of multivariate beta distribution (MBD) . Dirichlet distributions are commonly used as prior distributions in Bayesian statistics, and in fact, the Dirichlet distribution is the conjugate prior of the categorical distribution and multinomial distribution.$

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.

In probability theory, the Rice distribution or Rician distribution is the probability distribution of the magnitude of a circularly-symmetric bivariate normal random variable, possibly with non-zero mean (noncentral). It was named after Stephen O. Rice (1907–1986).

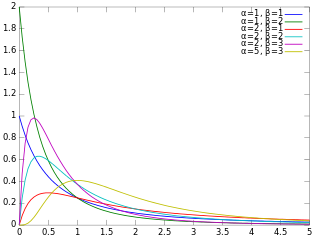
In probability theory and statistics, the beta prime distribution is an absolutely continuous probability distribution. If $has a beta distribution, then the odds has a beta prime distribution.$

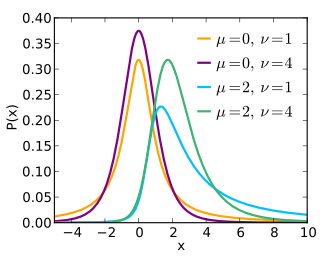
The noncentral t-distribution generalizes Student's t-distribution using a noncentrality parameter. Whereas the central probability distribution describes how a test statistic t is distributed when the difference tested is null, the noncentral distribution describes how t is distributed when the null is false. This leads to its use in statistics, especially calculating statistical power. The noncentral t-distribution is also known as the singly noncentral t-distribution, and in addition to its primary use in statistical inference, is also used in robust modeling for data.

In natural language processing, latent Dirichlet allocation (LDA) is a Bayesian network for modeling automatically extracted topics in textual corpora. The LDA is an example of a Bayesian topic model. In this, observations are collected into documents, and each word's presence is attributable to one of the document's topics. Each document will contain a small number of topics.

In statistics, the multivariate t-distribution is a multivariate probability distribution. It is a generalization to random vectors of the Student's t-distribution, which is a distribution applicable to univariate random variables. While the case of a random matrix could be treated within this structure, the matrix t-distribution is distinct and makes particular use of the matrix structure.

In statistics, the inverse Wishart distribution, also called the inverted Wishart distribution, is a probability distribution defined on real-valued positive-definite matrices. In Bayesian statistics it is used as the conjugate prior for the covariance matrix of a multivariate normal distribution.

Expected shortfall (ES) is a risk measure—a concept used in the field of financial risk measurement to evaluate the market risk or credit risk of a portfolio. The "expected shortfall at q% level" is the expected return on the portfolio in the worst $of cases. ES is an alternative to value at risk that is more sensitive to the shape of the tail of the loss distribution.$

In probability theory and statistics, the Dirichlet-multinomial distribution is a family of discrete multivariate probability distributions on a finite support of non-negative integers. It is also called the Dirichlet compound multinomial distribution (DCM) or multivariate Pólya distribution. It is a compound probability distribution, where a probability vector p is drawn from a Dirichlet distribution with parameter vector $, and an observation drawn from a multinomial distribution with probability vector p and number of trials n . The Dirichlet parameter vector captures the prior belief about the situation and can be seen as a pseudocount: observations of each outcome that occur before the actual data is collected. The compounding corresponds to a Pólya urn scheme. It is frequently encountered in Bayesian statistics, machine learning, empirical Bayes methods and classical statistics as an overdispersed multinomial distribution.$

In probability theory and statistics, the Conway–Maxwell–Poisson distribution is a discrete probability distribution named after Richard W. Conway, William L. Maxwell, and Siméon Denis Poisson that generalizes the Poisson distribution by adding a parameter to model overdispersion and underdispersion. It is a member of the exponential family, has the Poisson distribution and geometric distribution as special cases and the Bernoulli distribution as a limiting case.

<span class="mw-page-title-main">Lomax distribution</span>

The Lomax distribution, conditionally also called the Pareto Type II distribution, is a heavy-tail probability distribution used in business, economics, actuarial science, queueing theory and Internet traffic modeling. It is named after K. S. Lomax. It is essentially a Pareto distribution that has been shifted so that its support begins at zero.

In statistics, the complex Wishart distribution is a complex version of the Wishart distribution. It is the distribution of $times the sample Hermitian covariance matrix of zero-mean independent Gaussian random variables. It has support for Hermitian positive definite matrices.$

In probability theory, the stable count distribution is the conjugate prior of a one-sided stable distribution. This distribution was discovered by Stephen Lihn in his 2017 study of daily distributions of the S&P 500 and the VIX. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.

In probability theory and statistics, the Dirichlet negative multinomial distribution is a multivariate distribution on the non-negative integers. It is a multivariate extension of the beta negative binomial distribution. It is also a generalization of the negative multinomial distribution (NM(k, p)) allowing for heterogeneity or overdispersion to the probability vector. It is used in quantitative marketing research to flexibly model the number of household transactions across multiple brands.

References

↑ Tiao, George (1965). "The inverted Dirichlet distribution with applications". Journal of the American Statistical Association. 60 (311): 793–805. doi:10.1080/01621459.1965.10480828.
↑ Ghorbel, M. (2010). "On the inverted Dirichlet distribution". Communications in Statistics - Theory and Methods. 39: 21–37. doi:10.1080/03610920802627062. S2CID 122956752.
↑ Bdiri, Taoufik; Nizar, Bouguila (2012). "Positive vectors clustering using inverted Dirichlet finite mixture models". Expert Systems with Applications. 39 (2): 1869–1882. doi:10.1016/j.eswa.2011.08.063.
↑ Bdiri, Taoufik; Bouguila, Nizar (2011). "Learning Inverted Dirichlet Mixtures for Positive Data Clustering". Rough Sets, Fuzzy Sets, Data Mining and Granular Computing. Lecture Notes in Computer Science. Vol. 6743. pp. 265–272. doi:10.1007/978-3-642-21881-1_42. ISBN 978-3-642-21880-4.
↑ Bdiri, Taoufik; Bouguila, Nizar (2011). "An Infinite Mixture of Inverted Dirichlet Distributions". Neural Information Processing. Lecture Notes in Computer Science. Vol. 7063. pp. 71–78. doi:10.1007/978-3-642-24958-7_9. ISBN 978-3-642-24957-0.
↑ Bdiri, Taoufik; Nizar, Bouguila (2013). "Bayesian learning of inverted Dirichlet mixtures for SVM kernels generation" (PDF). Neural Computing and Applications. 23 (5): 1443–1458. doi:10.1007/s00521-012-1094-z. S2CID 254025619.
↑ Bdiri, Taoufik; Bouguila, Nizar; Ziou, Djemel (2014). "Object clustering and recognition using multi-finite mixtures for semantic classes and hierarchy modeling". Expert Systems with Applications. 41 (4): 1218–1235. doi:10.1016/j.eswa.2013.08.005.
↑ Bdiri, Taoufik; Bouguila, Nizar; Ziou, Djemel (2013). "Visual Scenes Categorization Using a Flexible Hierarchical Mixture Model Supporting Users Ontology". 2013 IEEE 25th International Conference on Tools with Artificial Intelligence. pp. 262–267. doi:10.1109/ICTAI.2013.48. ISBN 978-1-4799-2972-6. S2CID 1236111.

This statistics-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Tiao1965-1] Tiao, George (1965). "The inverted Dirichlet distribution with applications". Journal of the American Statistical Association. 60 (311): 793–805. doi:10.1080/01621459.1965.10480828.

[ghorbel2010-2] Ghorbel, M. (2010). "On the inverted Dirichlet distribution". Communications in Statistics - Theory and Methods. 39: 21–37. doi:10.1080/03610920802627062. S2CID 122956752.

[3] Bdiri, Taoufik; Nizar, Bouguila (2012). "Positive vectors clustering using inverted Dirichlet finite mixture models". Expert Systems with Applications. 39 (2): 1869–1882. doi:10.1016/j.eswa.2011.08.063.

[4] Bdiri, Taoufik; Bouguila, Nizar (2011). "Learning Inverted Dirichlet Mixtures for Positive Data Clustering". Rough Sets, Fuzzy Sets, Data Mining and Granular Computing. Lecture Notes in Computer Science. Vol. 6743. pp. 265–272. doi:10.1007/978-3-642-21881-1_42. ISBN 978-3-642-21880-4.

[5] Bdiri, Taoufik; Bouguila, Nizar (2011). "An Infinite Mixture of Inverted Dirichlet Distributions". Neural Information Processing. Lecture Notes in Computer Science. Vol. 7063. pp. 71–78. doi:10.1007/978-3-642-24958-7_9. ISBN 978-3-642-24957-0.

[6] Bdiri, Taoufik; Nizar, Bouguila (2013). "Bayesian learning of inverted Dirichlet mixtures for SVM kernels generation" (PDF). Neural Computing and Applications. 23 (5): 1443–1458. doi:10.1007/s00521-012-1094-z. S2CID 254025619.

[7] Bdiri, Taoufik; Bouguila, Nizar; Ziou, Djemel (2014). "Object clustering and recognition using multi-finite mixtures for semantic classes and hierarchy modeling". Expert Systems with Applications. 41 (4): 1218–1235. doi:10.1016/j.eswa.2013.08.005.

[8] Bdiri, Taoufik; Bouguila, Nizar; Ziou, Djemel (2013). "Visual Scenes Categorization Using a Flexible Hierarchical Mixture Model Supporting Users Ontology". 2013 IEEE 25th International Conference on Tools with Artificial Intelligence. pp. 262–267. doi:10.1109/ICTAI.2013.48. ISBN 978-1-4799-2972-6. S2CID 1236111.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]