An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word ἀξίωμα (axíōma), meaning 'that which is thought worthy or fit' or 'that which commends itself as evident'.

In computing, floating-point arithmetic (FP) is arithmetic that represents real numbers approximately, using an integer with a fixed precision, called the significand, scaled by an integer exponent of a fixed base. For example, 12.345 can be represented as a base-ten floating-point number:
IEEE 754-1985 was an industry standard for representing floating-point numbers in computers, officially adopted in 1985 and superseded in 2008 by IEEE 754-2008, and then again in 2019 by minor revision IEEE 754-2019. During its 23 years, it was the most widely used format for floating-point computation. It was implemented in software, in the form of floating-point libraries, and in hardware, in the instructions of many CPUs and FPUs. The first integrated circuit to implement the draft of what was to become IEEE 754-1985 was the Intel 8087.

Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division. The result of a multiplication operation is called a product.
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano. These axioms have been used nearly unchanged in a number of metamathematical investigations, including research into fundamental questions of whether number theory is consistent and complete.
In computing, NaN, standing for Not a Number, is a member of a numeric data type that can be interpreted as a value that is undefined or unrepresentable, especially in floating-point arithmetic. Systematic use of NaNs was introduced by the IEEE 754 floating-point standard in 1985, along with the representation of other non-finite quantities such as infinities.
Double-precision floating-point format is a floating-point number format, usually occupying 64 bits in computer memory; it represents a wide dynamic range of numeric values by using a floating radix point.
In classical deductive logic, a consistent theory is one that does not lead to a logical contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if it has a model, i.e., there exists an interpretation under which all formulas in the theory are true. This is the sense used in traditional Aristotelian logic, although in contemporary mathematical logic the term satisfiable is used instead. The syntactic definition states a theory is consistent if there is no formula such that both and its negation are elements of the set of consequences of . Let be a set of closed sentences and the set of closed sentences provable from under some formal deductive system. The set of axioms is consistent when for no formula .
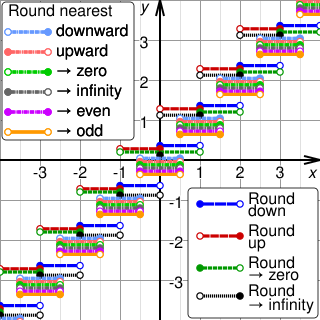
Rounding means replacing a number with an approximate value that has a shorter, simpler, or more explicit representation. For example, replacing $23.4476 with $23.45, the fraction 312/937 with 1/3, or the expression √2 with 1.414.

In mathematics, division by zero is division where the divisor (denominator) is zero. Such a division can be formally expressed as , where a is the dividend (numerator). In ordinary arithmetic, the expression has no meaning, as there is no number that, when multiplied by 0, gives a ; thus, division by zero is undefined. Since any number multiplied by zero is zero, the expression is also undefined; when it is the form of a limit, it is an indeterminate form. Historically, one of the earliest recorded references to the mathematical impossibility of assigning a value to is contained in Anglo-Irish philosopher George Berkeley's criticism of infinitesimal calculus in 1734 in The Analyst.
In axiomatic set theory and the branches of mathematics and philosophy that use it, the axiom of infinity is one of the axioms of Zermelo–Fraenkel set theory. It guarantees the existence of at least one infinite set, namely a set containing the natural numbers. It was first published by Ernst Zermelo as part of his set theory in 1908.
The IEEE Standard for Floating-Point Arithmetic is a technical standard for floating-point arithmetic established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The standard addressed many problems found in the diverse floating-point implementations that made them difficult to use reliably and portably. Many hardware floating-point units use the IEEE 754 standard.
Internal set theory (IST) is a mathematical theory of sets developed by Edward Nelson that provides an axiomatic basis for a portion of the nonstandard analysis introduced by Abraham Robinson. Instead of adding new elements to the real numbers, Nelson's approach modifies the axiomatic foundations through syntactic enrichment. Thus, the axioms introduce a new term, "standard", which can be used to make discriminations not possible under the conventional ZFC axioms for sets. Thus, IST is an enrichment of ZFC: all axioms of ZFC are satisfied for all classical predicates, while the new unary predicate "standard" satisfies three additional axioms I, S, and T. In particular, suitable nonstandard elements within the set of real numbers can be shown to have properties that correspond to the properties of infinitesimal and unlimited elements.
In mathematical logic, New Foundations (NF) is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name. Much of this entry discusses NFU, an important variant of NF due to Jensen (1969) and clarified by Holmes (1998). In 1940 and in a revision in 1951, Quine introduced an extension of NF sometimes called "Mathematical Logic" or "ML", that included proper classes as well as sets.
The term arithmetic underflow is a condition in a computer program where the result of a calculation is a number of more precise absolute value than the computer can actually represent in memory on its central processing unit (CPU).
In mathematics, Robinson arithmetic is a finitely axiomatized fragment of first-order Peano arithmetic (PA), first set out by R. M. Robinson in 1950. It is usually denoted Q. Q is almost PA without the axiom schema of mathematical induction. Q is weaker than PA but it has the same language, and both theories are incomplete. Q is important and interesting because it is a finitely axiomatized fragment of PA that is recursively incompletable and essentially undecidable.
In mathematical logic, Heyting arithmetic is an axiomatization of arithmetic in accordance with the philosophy of intuitionism. It is named after Arend Heyting, who first proposed it.
Signed zero is zero with an associated sign. In ordinary arithmetic, the number 0 does not have a sign, so that −0, +0 and 0 are identical. However, in computing, some number representations allow for the existence of two zeros, often denoted by −0 and +0, regarded as equal by the numerical comparison operations but with possible different behaviors in particular operations. This occurs in the sign and magnitude and ones' complement signed number representations for integers, and in most floating-point number representations. The number 0 is usually encoded as +0, but can be represented by either +0 or −0.
Single-precision floating-point format is a computer number format, usually occupying 32 bits in computer memory; it represents a wide dynamic range of numeric values by using a floating radix point.

In mathematics, division by infinity is division where the divisor (denominator) is infinity. In ordinary arithmetic, this does not have a well-defined meaning, since infinity is a mathematical concept that does not correspond to a specific number, and moreover, there is no nonzero real number that, when added to itself an infinite number of times, gives a finite number. However, "dividing by infinity" can be given meaning as an informal way of expressing the limit of dividing a number by larger and larger divisors.











































