Jeannine Mosely

Last updated

Jeannine Mosely (born May 16, 1953 in Pittsburgh, PA) holds a Ph.D. in EECS from the Massachusetts Institute of Technology, and is known for her work as an origami artist. [1] She is best known for her modular origami designs, especially her work using business cards. She has organized several crowd-sourced origami projects built from tens of thousands of business cards involving hundred of volunteers for each project. She is also known for her minimalist origami designs (such as her fourfold alphabet), curved crease models, and her invention of "or-egg-ami" models made from egg cartons.

Contents

Education and engineering career

Mosely earned a B.A. in mathematics and a B.S. in electrical engineering from the University of Illinois at Urbana-Champaign and a M.S. and Ph.D. in electrical engineering and computer science from the Massachusetts Institute of Technology. For her master's degree she developed algorithms for time-division multiple access (used in cell-phone technology). [2] For her doctorate she developed flow-control algorithms for handling internet traffic. After finishing her degree, Mosely taught as a visiting lecturer for a year at the University of California, Berkeley in the EECS Department. Subsequently she worked at ICAD, Inc. from 1986 to 1999, developing geometric modeling algorithms for computer-aided design.

Origami


Mosely has created several, large, crowd sourced, origami projects with business cards, as well as many smaller business card models. In 1994 she invented a method for linking traditional business card cubes together into structures that could be very large. In 1995 she launched a project to construct a level 3 approximation to the fractal called the Menger Sponge using these cubes. The project was finished in 2005 with 66,048 cards folded and assembled by Mosely and about 200 volunteers. [3]

In 2008 she was commissioned by First Night Worcester (MA) to develop a project to be a part Worcester's New Year's Eve celebration. Worcester's Union Station was chosen as the model to be built. Mosely made a 3D computer model of the station, which was then developed into the resulting business card model. Several hundred Worcester school children assisted by student volunteers from Worcester Polytechnic Institute folded cubes and helped construct the finished model which incorporated over 60,000 cards. [4]

In 2012, the University of Southern California Libraries commissioned Mosely to co-lead a project in conjunction with Margaret Wertheim, their resident Discovery Fellow, [5] to engage hundreds members of the USC community in building the Mosely Snowflake Sponge, another fractal model, from approximately 49,000 business cards. [6] [7] The Mosely Snowflake Sponge, a member of the same family of fractals as the Menger Sponge, was discovered by Mosely in 2006 while she was exhibiting her model of that original fractal at Machine Project gallery in Los Angeles. [8] The catalog for the Machine-Menger show was published as a small artist's book "A Field Guide to the Business Card Menger Sponge," co-written by Mosely and Wertheim, the exhibition curator. [9] The texts and images of this book are available as an online exhibit [10] at the Institute For Figuring.

Mosely has also developed mathematical techniques for designing and analyzing curved origami models such as her "Orb," [11] "Bud," [12] and "Sails." [13] Sails is a tessellation piece created from a single sheet of white watercolor paper and made up of a repeating pattern of overlapping triangles that evokes billowing sails. [14] In 2019-2020, "Sails" was on display at the Math Unfolded exhibition at the National Museum of Mathematics. [15] [16]

In 2007, Mosely began designing origami-like polyhedral models using egg cartons. She calls this technique "or-egg-ami." In 2012 one of these models was bronzed and gilded by sculptor Kevin Box with help from artist Dick Esterle. The completed sculpture, titled "Waxing Gibbous," was displayed at the Bridges Math Art Conference. [17]

See also

Related Research Articles

<span class="mw-page-title-main">Fractal</span> Infinitely detailed mathematical structure

In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory.

<span class="mw-page-title-main">Fractal art</span>

Fractal art is a form of algorithmic art created by calculating fractal objects and representing the calculation results as still digital images, animations, and media. Fractal art developed from the mid-1980s onwards. It is a genre of computer art and digital art which are part of new media art. The mathematical beauty of fractals lies at the intersection of generative art and computer art. They combine to produce a type of abstract art.

<span class="mw-page-title-main">Origami</span> Traditional Japanese art of paper folding

Origami is the Japanese art of paper folding. In modern usage, the word "origami" is often used as an inclusive term for all folding practices, regardless of their culture of origin. The goal is to transform a flat square sheet of paper into a finished sculpture through folding and sculpting techniques. Modern origami practitioners generally discourage the use of cuts, glue, or markings on the paper. Origami folders often use the Japanese word kirigami to refer to designs which use cuts.

<span class="mw-page-title-main">Pattern</span> Regularity in sensory qualia or abstract ideas

A pattern is a regularity in the world, in human-made design, or in abstract ideas. As such, the elements of a pattern repeat in a predictable manner. A geometric pattern is a kind of pattern formed of geometric shapes and typically repeated like a wallpaper design.

<span class="mw-page-title-main">Menger sponge</span> Three-dimensional fractal

In mathematics, the Menger sponge is a fractal curve. It is a three-dimensional generalization of the one-dimensional Cantor set and two-dimensional Sierpinski carpet. It was first described by Karl Menger in 1926, in his studies of the concept of topological dimension.

<span class="mw-page-title-main">Mathematics of paper folding</span> Overview of the mathematics of paper folding

The discipline of origami or paper folding has received a considerable amount of mathematical study. Fields of interest include a given paper model's flat-foldability, and the use of paper folds to solve up-to cubic mathematical equations.

<span class="mw-page-title-main">Modular origami</span>

Modular origami or unit origami is a paperfolding technique which uses two or more sheets of paper to create a larger and more complex structure than would be possible using single-piece origami techniques. Each individual sheet of paper is folded into a module, or unit, and then modules are assembled into an integrated flat shape or three-dimensional structure, usually by inserting flaps into pockets created by the folding process. These insertions create tension or friction that holds the model together.

<span class="mw-page-title-main">Erik Demaine</span> Professor of computer science

Erik D. Demaine is a professor of computer science at the Massachusetts Institute of Technology and a former child prodigy.

<span class="mw-page-title-main">Daina Taimiņa</span> Latvian mathematician

Daina Taimiņa is a Latvian mathematician, retired adjunct associate professor of mathematics at Cornell University, known for discovering a groundbreaking way of modelling hyperbolic planes by crocheting objects to illustrate hyperbolic space and innovative use of them teaching geometry.

<span class="mw-page-title-main">Fractal curve</span> Mathematical curve whose shape is a fractal

A fractal curve is, loosely, a mathematical curve whose shape retains the same general pattern of irregularity, regardless of how high it is magnified, that is, its graph takes the form of a fractal. In general, fractal curves are nowhere rectifiable curves — that is, they do not have finite length — and every subarc longer than a single point has infinite length.

<span class="mw-page-title-main">Margaret Wertheim</span>

Margaret Wertheim is an Australian-born science writer, curator, and artist based in the United States. She is the author of books on the cultural history of physics, and has written about science, including for the New York Times, Los Angeles Times, Guardian, Aeon and Cabinet. Wertheim and her twin sister, Christine Wertheim, are co-founders of the Institute For Figuring (IFF), a Los Angeles-based non-profit organization though which they create projects at the intersection of art, science and mathematics. Their IFF projects include their Crochet Coral Reef, which has been shown at the 2019 Venice Biennale, Hayward Gallery (London), Museum of Arts and Design (NYC), and the Smithsonian's National Museum of Natural History. For her work with public science engagement, Wertheim won the 2016 Klopsteg Memorial Award from the American Association of Physics Teachers and Australia's Scientia Medal (2017).

<span class="mw-page-title-main">Institute For Figuring</span>

The Institute For Figuring (IFF) is an organization based in Los Angeles, California that promotes the public understanding of the poetic and aesthetic dimensions of science, mathematics and the technical arts. Founded by Margaret Wertheim and Christine Wertheim, the institute hosts public lectures and exhibitions, publishes books and maintains a website.

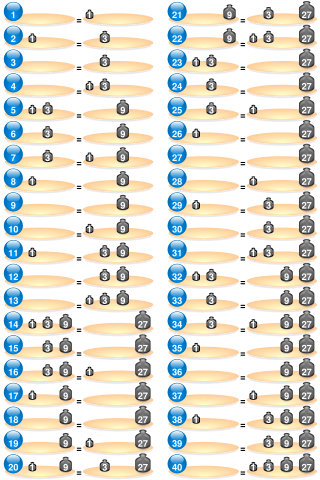
<span class="mw-page-title-main">Power of three</span> Exponentiation

In mathematics, a power of three is a number of the form 3n where n is an integer – that is, the result of exponentiation with number three as the base and integer n as the exponent.

<span class="mw-page-title-main">Fractal-generating software</span>

Fractal-generating software is any type of graphics software that generates images of fractals. There are many fractal generating programs available, both free and commercial. Mobile apps are available to play or tinker with fractals. Some programmers create fractal software for themselves because of the novelty and because of the challenge in understanding the related mathematics. The generation of fractals has led to some very large problems for pure mathematics.

<span class="mw-page-title-main">Mathematics and art</span> Relationship between mathematics and art

Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.

Robert "Bob" Stephen Strichartz was an American mathematician who specialized in mathematical analysis.

Radhika Nagpal is an American computer scientist and researcher in the fields of self-organising computer systems, biologically-inspired robotics, and biological multi-agent systems. She is the Fred Kavli Professor of Computer Science at Harvard University and the Harvard School of Engineering and Applied Sciences. She is also a Core Faculty Member of the Harvard Wyss Institute for Biologically Inspired Engineering. In 2017, Nagpal co-founded a robotics company under the name of Root Robotics. This educational company works to create many different opportunities for those unable to code to learn how.

<span class="mw-page-title-main">Mosely snowflake</span>

The Mosely snowflake is a Sierpiński–Menger type of fractal obtained in two variants either by the operation opposite to creating the Sierpiński-Menger snowflake or Cantor dust i.e. not by leaving but by removing eight of the smaller 1/3-scaled corner cubes and the central one from each cube left from the previous recursion (lighter) or by removing only corner cubes (heavier). In one dimension this operation is trivial and converges only to single point. It resembles the original water snowflake of snow. By the construction the Hausdorff dimension of the lighter snowflake is

<i>Mathemalchemy</i>

Mathemalchemy is a traveling art installation dedicated to a celebration of the intersection of art and mathematics. It is a collaborative work led by Duke University mathematician Ingrid Daubechies and fiber artist Dominique Ehrmann. The cross-disciplinary team of 24 people, who collectively built the installation during the calendar years 2020 and 2021, includes artists, mathematicians, and craftspeople who employed a wide variety of materials to illustrate, amuse, and educate the public on the wonders, mystery, and beauty of mathematics. Including the core team of 24, about 70 people contributed in some way to the realization of Mathemalchemy.

References

  1. ↑ Karlin, Susan (1 May 2008). "Jeannine Mosely: Paper Sculptor". IEEE Spectrum: Technology, Engineering, and Science News. Retrieved 2017-03-10.
  2. ↑ Humblet, P. A.; Mosely, Jeannine (1985). "A class of efficient contention resolution algorithms for multiple access channels". Laboratory for Information and Decision Systems, Massachusetts Institute of Technology. hdl:1721.1/1035.{{cite journal}}: Cite journal requires |journal= (help)
  3. ↑ Friedman, Rick (2005-06-21). "Fractal Mathematics With Business Cards". The New York Times. ISSN   0362-4331 . Retrieved 2017-03-10.
  4. ↑ zke2208 (2008-12-11). "YOUcubed origami to be folded into First Night". Worcester Mag. Archived from the original on 2017-03-12. Retrieved 2017-03-10.
  5. ↑ Wertheim, Margaret (September 20, 2012). "Mosely Snowflake Sponge at the USC Libraries". Institute For Figuring. Retrieved 2020-05-03.
  6. ↑ Masters, Nathan (January 20, 2012). "Help Build the Mosely Snowflake Sponge, a 3-D Fractal Object, for the First Time in the Universe". USC Libraries. Retrieved 2017-03-10.
  7. ↑ Wade, Lizzie. "Folding Fractal Art from 49,000 Business Cards". Wired . Retrieved 2017-03-10.
  8. ↑ Wertheim, Margaret (August 26, 2006). "The Business Card Menger Sponge at Machine Project". Institute For Figuring. Retrieved 2020-05-03.
  9. ↑ Mosely, Wertheim. "A Field Guide to the Business Card Menger Sponge". Institute For Figuring Press. Retrieved 2020-05-03.
  10. ↑ Mosely, Wertheim. "Business Card Menger Sponge Exhibit". Institute For Figuring. Retrieved 2020-05-03.
  11. ↑ "Business Card Origami Orb". Origami Resource Center. Retrieved 2017-03-10.
  12. ↑ "How to Make Your Own Square-Based Origami Bud". Editorial. Cabinet (17). Spring 2005. Retrieved 2017-03-10.
  13. ↑ liranik (15 August 2008). "Sails (curved origami) by Jeannine Mosely (paper)". Flickr . Retrieved 2017-03-10.
  14. ↑ McArthur, Meher; Lang, Robert J. (2017). New Expressions in Origami Art: Masterworks from 25 Leading Paper Artists. Tuttle Publishing. p. 142. ISBN   9780804846776.
  15. ↑ "Meet the Artist: Origami Artist Jeannine Mosely". National Museum of Mathematics. Retrieved 2021-03-31.{{cite web}}: CS1 maint: url-status (link)
  16. ↑ "Math Unfolded: An Exhibit of Mathematical Origami Art" . Retrieved 2021-03-31.{{cite web}}: CS1 maint: url-status (link)
  17. ↑ "Jeannine Mosely (with collaborators Dick Esterle, Kevin Box for "Waxing Gibbous")". Mathematical Art Galleries. Retrieved 2017-03-10.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.