Joint Probabilistic Data Association Filter

Last updated

The joint probabilistic data-association filter (JPDAF) [1] is a statistical approach to the problem of plot association (target-measurement assignment) in a target tracking algorithm. Like the probabilistic data association filter (PDAF), rather than choosing the most likely assignment of measurements to a target (or declaring the target not detected or a measurement to be a false alarm), the PDAF takes an expected value, which is the minimum mean square error (MMSE) estimate for the state of each target. At each time, it maintains its estimate of the target state as the mean and covariance matrix of a multivariate normal distribution. However, unlike the PDAF, which is only meant for tracking a single target in the presence of false alarms and missed detections, the JPDAF can handle multiple target tracking scenarios. A derivation of the JPDAF is given in. [2]

Contents

The JPDAF is one of several techniques for radar target tracking and for target tracking in the field of computer vision.

The coalescence problem

A common problem observed with the JPDAF is that estimates of closely spaced targets tend to coalesce over time. [3] [4] This is because the MMSE estimate is typically undesirable when target identity is uncertain. [5]

Variants of the JPDAF algorithm have been made that try to avoid track coalescence. For example, the Set JPDAF [6] uses an approximate minimum mean optimal sub pattern assignment (MMOSPA) instead of an approximate MMSE estimator. The JPDAF*, [7] modifies how the target-measurement association probabilities are computed, and variants of the global nearest-neighbor JPDAF (GNN-JPDAF) (a best-hypothesis tracker) [8] use the global nearest neighbor (GNN) estimate in place of the mean but compute the covariance matrix as in the normal JPDAF: as a mean-squared error matrix.

Implementations

Related Research Articles

Linear prediction is a mathematical operation where future values of a discrete-time signal are estimated as a linear function of previous samples.

<span class="mw-page-title-main">Kalman filter</span> Algorithm that estimates unknowns from a series of measurements over time

In statistics and control theory, Kalman filtering is an algorithm that uses a series of measurements observed over time, including statistical noise and other inaccuracies, to produce estimates of unknown variables that tend to be more accurate than those based on a single measurement, by estimating a joint probability distribution over the variables for each time-step. The filter is constructed as a mean squared error minimiser, but an alternative derivation of the filter is also provided showing how the filter relates to maximum likelihood statistics. The filter is named after Rudolf E. Kálmán.

<span class="mw-page-title-main">Synthetic-aperture radar</span> Form of radar used to create images of landscapes

Synthetic-aperture radar (SAR) is a form of radar that is used to create two-dimensional images or three-dimensional reconstructions of objects, such as landscapes. SAR uses the motion of the radar antenna over a target region to provide finer spatial resolution than conventional stationary beam-scanning radars. SAR is typically mounted on a moving platform, such as an aircraft or spacecraft, and has its origins in an advanced form of side looking airborne radar (SLAR). The distance the SAR device travels over a target during the period when the target scene is illuminated creates the large synthetic antenna aperture. Typically, the larger the aperture, the higher the image resolution will be, regardless of whether the aperture is physical or synthetic – this allows SAR to create high-resolution images with comparatively small physical antennas. For a fixed antenna size and orientation, objects which are further away remain illuminated longer – therefore SAR has the property of creating larger synthetic apertures for more distant objects, which results in a consistent spatial resolution over a range of viewing distances.

<span class="mw-page-title-main">Simultaneous localization and mapping</span> Computational navigational technique used by robots and autonomous vehicles

Simultaneous localization and mapping (SLAM) is the computational problem of constructing or updating a map of an unknown environment while simultaneously keeping track of an agent's location within it. While this initially appears to be a chicken or the egg problem, there are several algorithms known to solve it in, at least approximately, tractable time for certain environments. Popular approximate solution methods include the particle filter, extended Kalman filter, covariance intersection, and GraphSLAM. SLAM algorithms are based on concepts in computational geometry and computer vision, and are used in robot navigation, robotic mapping and odometry for virtual reality or augmented reality.

<span class="mw-page-title-main">Sensor fusion</span> Combining of sensor data from disparate sources

Sensor fusion is the process of combining sensor data or data derived from disparate sources so that the resulting information has less uncertainty than would be possible if these sources were used individually. For instance, one could potentially obtain a more accurate location estimate of an indoor object by combining multiple data sources such as video cameras and WiFi localization signals. The term uncertainty reduction in this case can mean more accurate, more complete, or more dependable, or refer to the result of an emerging view, such as stereoscopic vision.

The fast Kalman filter (FKF), devised by Antti Lange (born 1941), is an extension of the Helmert–Wolf blocking (HWB) method from geodesy to safety-critical real-time applications of Kalman filtering (KF) such as GNSS navigation up to the centimeter-level of accuracy and satellite imaging of the Earth including atmospheric tomography.

The condensation algorithm is a computer vision algorithm. The principal application is to detect and track the contour of objects moving in a cluttered environment. Object tracking is one of the more basic and difficult aspects of computer vision and is generally a prerequisite to object recognition. Being able to identify which pixels in an image make up the contour of an object is a non-trivial problem. Condensation is a probabilistic algorithm that attempts to solve this problem.

In statistics and signal processing, a minimum mean square error (MMSE) estimator is an estimation method which minimizes the mean square error (MSE), which is a common measure of estimator quality, of the fitted values of a dependent variable. In the Bayesian setting, the term MMSE more specifically refers to estimation with quadratic loss function. In such case, the MMSE estimator is given by the posterior mean of the parameter to be estimated. Since the posterior mean is cumbersome to calculate, the form of the MMSE estimator is usually constrained to be within a certain class of functions. Linear MMSE estimators are a popular choice since they are easy to use, easy to calculate, and very versatile. It has given rise to many popular estimators such as the Wiener–Kolmogorov filter and Kalman filter.

Video tracking is the process of locating a moving object over time using a camera. It has a variety of uses, some of which are: human-computer interaction, security and surveillance, video communication and compression, augmented reality, traffic control, medical imaging and video editing. Video tracking can be a time-consuming process due to the amount of data that is contained in video. Adding further to the complexity is the possible need to use object recognition techniques for tracking, a challenging problem in its own right.

In wireless communications, channel state information (CSI) is the known channel properties of a communication link. This information describes how a signal propagates from the transmitter to the receiver and represents the combined effect of, for example, scattering, fading, and power decay with distance. The method is called channel estimation. The CSI makes it possible to adapt transmissions to current channel conditions, which is crucial for achieving reliable communication with high data rates in multiantenna systems.

A radar tracker is a component of a radar system, or an associated command and control (C2) system, that associates consecutive radar observations of the same target into tracks. It is particularly useful when the radar system is reporting data from several different targets or when it is necessary to combine the data from several different radars or other sensors.

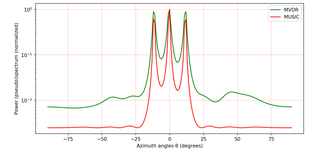
<span class="mw-page-title-main">MUSIC (algorithm)</span> Algorithm used for frequency estimation and radio direction finding

MUSIC is an algorithm used for frequency estimation and radio direction finding.

GPS/INS is the use of GPS satellite signals to correct or calibrate a solution from an inertial navigation system (INS). The method is applicable for any GNSS/INS system.

An alpha beta filter is a simplified form of observer for estimation, data smoothing and control applications. It is closely related to Kalman filters and to linear state observers used in control theory. Its principal advantage is that it does not require a detailed system model.

In estimation theory, the extended Kalman filter (EKF) is the nonlinear version of the Kalman filter which linearizes about an estimate of the current mean and covariance. In the case of well defined transition models, the EKF has been considered the de facto standard in the theory of nonlinear state estimation, navigation systems and GPS.

The Probabilistic Data Association Filter (PDAF) is a statistical approach to the problem of plot association in a target tracking algorithm. Rather than choosing the most likely assignment of measurements to a target, the PDAF takes an expected value, which is the minimum mean square error (MMSE) estimate. The PDAF on its own does not confirm nor terminate tracks.

Covariance intersection (CI) is an algorithm for combining two or more estimates of state variables in a Kalman filter when the correlation between them is unknown.

Masreliez theorem describes a recursive algorithm within the technology of extended Kalman filter, named after the Swedish-American physicist John Masreliez, who is its author. The algorithm estimates the state of a dynamic system with the help of often incomplete measurements marred by distortion.

<span class="mw-page-title-main">Yaakov Bar-Shalom</span> Electrical engineer

Yaakov Bar-Shalom is a researcher in tracking and sensor fusion. His work is associated with MS-MTT and IMM (interacting-multiple-model) estimator.

SAMV is a parameter-free superresolution algorithm for the linear inverse problem in spectral estimation, direction-of-arrival (DOA) estimation and tomographic reconstruction with applications in signal processing, medical imaging and remote sensing. The name was coined in 2013 to emphasize its basis on the asymptotically minimum variance (AMV) criterion. It is a powerful tool for the recovery of both the amplitude and frequency characteristics of multiple highly correlated sources in challenging environments. Applications include synthetic-aperture radar, computed tomography scan, and magnetic resonance imaging (MRI).

References

  1. ↑ Bar-Shalom, Yaakov; Daum, Fred; Huang, Jim (December 2009). "The probabilistic data association filter". IEEE Control Systems Magazine. 29 (6): 82–100. doi:10.1109/MCS.2009.934469. S2CID   6875122.
  2. ↑ Bar-Shalom, Yaakov; Li, Xiao-Rong (1995). Multitarget-multisensor tracking : principles and techniques, 1995. Yaakov Bar-Shalom. ISBN   978-0964831209.
  3. ↑ Fitzgerald, Robert (November 1985). "Track Biases and Coalescence with Probabilistic Data Association". IEEE Transactions on Aerospace and Electronic Systems. AES-21 (6): 822–825. Bibcode:1985ITAES..21..822F. doi:10.1109/TAES.1985.310670. S2CID   6544485.
  4. ↑ Bar-Shalom, Yaakov (1986). "Comments on "Track Biases and Coalescence with Probabilistic Data Association"". IEEE Transactions on Aerospace and Electronic Systems. AES-22 (5): 661–662. Bibcode:1986ITAES..22..661.. doi:10.1109/TAES.1986.310734.
  5. ↑ Crouse, David (23 May 2013). Advances in displaying uncertain estimates of multiple targets. Proceeding of SPIE 8745, Signal Processing, Sensor Fusion, and Target Recognition XXII. Baltimore.
  6. ↑ Svensson, Lennart; Svensson, Daniel; Willett, Peter (July 2009). Set JPDA algorithm for tracking unordered sets of targets. Proceedings of the 12th International Conference of Information Fusion. Seattle. pp. 1187–1194.
  7. ↑ Blom, H.A.P.; Bloem, E.A. (2000). "Probabilistic data association avoiding track coalescence". IEEE Transactions on Automatic Control. 45 (2): 247–259. doi:10.1109/9.839947.
  8. ↑ Drummond, Oliver (October 1999). Best hypothesis target tracking and sensor fusion. Proceedings of SPIE: Signal and Data Processing of Small Targets Conference. Denver. pp. 586–600.
  9. ↑ "Tracker Component Library". Matlab Repository. Retrieved January 5, 2019.
  10. ↑ "Stone Soup Github Repo". GitHub .
  11. ↑ "Stone Soup JPDA Tutorial Docs".
  12. ↑ "Stone Soup JPDA Tutorial Code". GitHub .


This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.