In mathematics, more specifically in functional analysis, a Banach space is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well-defined limit that is within the space.

In geometry, a set of points is convex if it contains every line segment between two points in the set. Equivalently, a convex set or a convex region is a set that intersects every line in a line segment, single point, or the empty set. For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.
The Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a vector subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed vector space to make the study of the dual space "interesting". Another version of the Hahn–Banach theorem is known as the Hahn–Banach separation theorem or the hyperplane separation theorem, and has numerous uses in convex geometry.
In mathematics, a topological space is called separable if it contains a countable, dense subset; that is, there exists a sequence of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.

In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.

In Euclidean geometry, linear separability is a property of two sets of points. This is most easily visualized in two dimensions by thinking of one set of points as being colored blue and the other set of points as being colored red. These two sets are linearly separable if there exists at least one line in the plane with all of the blue points on one side of the line and all the red points on the other side. This idea immediately generalizes to higher-dimensional Euclidean spaces if the line is replaced by a hyperplane.

In geometry, a convex polygon is a polygon that is the boundary of a convex set. This means that the line segment between two points of the polygon is contained in the union of the interior and the boundary of the polygon. In particular, it is a simple polygon. Equivalently, a polygon is convex if every line that does not contain any edge intersects the polygon in at most two points.

In convex geometry and vector algebra, a convex combination is a linear combination of points where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the count of the weights as in a standard weighted average.
Carathéodory's theorem is a theorem in convex geometry. It states that if a point lies in the convex hull of a set , then lies in some -dimensional simplex with vertices in . Equivalently, can be written as the convex combination of at most points in . Additionally, can be written as the convex combination of at most extremal points in , as non-extremal points can be removed from without changing the membership of in the convex hull.

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.

In geometry, Radon's theorem on convex sets, published by Johann Radon in 1921, states that:
Any set of d + 2 points in Rd can be partitioned into two sets whose convex hulls intersect.

Helly's theorem is a basic result in discrete geometry on the intersection of convex sets. It was discovered by Eduard Helly in 1913, but not published by him until 1923, by which time alternative proofs by Radon (1921) and König (1922) had already appeared. Helly's theorem gave rise to the notion of a Helly family.
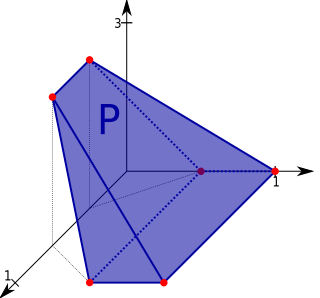
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the -dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.

In mathematics, the "happy ending problem" is the following statement:

In the mathematical theory of functional analysis, the Krein–Milman theorem is a proposition about compact convex sets in locally convex topological vector spaces (TVSs).
In mathematics, Choquet theory, named after Gustave Choquet, is an area of functional analysis and convex analysis concerned with measures which have support on the extreme points of a convex set C. Roughly speaking, every vector of C should appear as a weighted average of extreme points, a concept made more precise by generalizing the notion of weighted average from a convex combination to an integral taken over the set E of extreme points. Here C is a subset of a real vector space V, and the main thrust of the theory is to treat the cases where V is an infinite-dimensional topological vector space along lines similar to the finite-dimensional case. The main concerns of Gustave Choquet were in potential theory. Choquet theory has become a general paradigm, particularly for treating convex cones as determined by their extreme rays, and so for many different notions of positivity in mathematics.

In geometry, the hyperplane separation theorem is a theorem about disjoint convex sets in n-dimensional Euclidean space. There are several rather similar versions. In one version of the theorem, if both these sets are closed and at least one of them is compact, then there is a hyperplane in between them and even two parallel hyperplanes in between them separated by a gap. In another version, if both disjoint convex sets are open, then there is a hyperplane in between them, but not necessarily any gap. An axis which is orthogonal to a separating hyperplane is a separating axis, because the orthogonal projections of the convex bodies onto the axis are disjoint.

The Shapley–Folkman lemma is a result in convex geometry that describes the Minkowski addition of sets in a vector space. It is named after mathematicians Lloyd Shapley and Jon Folkman, but was first published by the economist Ross M. Starr.

Combinatorial Geometry in the Plane is a book in discrete geometry. It was translated from a German-language book, Kombinatorische Geometrie in der Ebene, which its authors Hugo Hadwiger and Hans Debrunner published through the University of Geneva in 1960, expanding a 1955 survey paper that Hadwiger had published in L'Enseignement mathématique. Victor Klee translated it into English, and added a chapter of new material. It was published in 1964 by Holt, Rinehart and Winston, and republished in 1966 by Dover Publications. A Russian-language edition, Комбинаторная геометрия плоскости, translated by I. M. Jaglom and including a summary of the new material by Klee, was published by Nauka in 1965. The Basic Library List Committee of the Mathematical Association of America has recommended its inclusion in undergraduate mathematics libraries.















