In astronomy, a double planet is a binary satellite system where both objects are planets, or planetary-mass objects, and whose joint barycenter is external to both planetary bodies.
Known Space is the fictional setting of about a dozen science fiction novels and several collections of short stories by American writer Larry Niven. It has also become a shared universe in the spin-off Man-Kzin Wars anthologies. The Internet Speculative Fiction Database (ISFDB) catalogs all works set in the fictional universe that includes Known Space under the series name Tales of Known Space, which was the title of a 1975 collection of Niven's short stories. The first-published work in the series, which was Niven's first published piece, was "The Coldest Place", in the December 1964 issue of If magazine, edited by Frederik Pohl. This was the first-published work in the 1975 collection.
In celestial mechanics, the Lagrange points are points of equilibrium for small-mass objects under the gravitational influence of two massive orbiting bodies. Mathematically, this involves the solution of the restricted three-body problem.
In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion.
Ringworld is a 1970 science fiction novel by Larry Niven, set in his Known Space universe and considered a classic of science fiction literature. Ringworld tells the story of Louis Wu and his companions on a mission to the Ringworld, an enormous rotating ring, an alien construct in space 186 million miles in diameter. Niven later wrote three sequel novels and then cowrote, with Edward M. Lerner, four prequels and a final sequel; the five latter novels constitute the Fleet of Worlds series. All the novels in the Ringworld series tie into numerous other books set in Known Space. Ringworld won the Nebula Award in 1970, as well as both the Hugo Award and Locus Award in 1971.
The Ringworld science fiction role-playing game was published by Chaosium in 1984, using the Basic Role-Playing system for its rules and Larry Niven's Ringworld novels as a setting.
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics to astronomical objects, such as stars and planets, to produce ephemeris data.
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets, satellites, and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and the law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.
Pierson's Puppeteers, often known just as Puppeteers, are a fictional alien race from American author Larry Niven's Known Space books. The race first appeared in Niven’s novella Neutron Star.
The Hill sphere is a common model for the calculation of a gravitational sphere of influence. It is the most commonly used model to calculate the spatial extent of gravitational influence of an astronomical body (m) in which it dominates over the gravitational influence of other bodies, particularly a primary (M). It is sometimes confused with other models of gravitational influence, such as the Laplace sphere or being called the Roche sphere, the latter causing confusion with the Roche limit. It was defined by the American astronomer George William Hill, based on the work of the French astronomer Édouard Roche.
An Alderson disk is a hypothetical artificial astronomical megastructure, like Larry Niven's Ringworld and the Dyson sphere. The disk is a giant platter with a thickness of several thousand miles. The Sun rests in the hole at the center of the disk. The outer perimeter of an Alderson disk would be roughly equivalent to the orbit of Mars or Jupiter. According to the proposal, a sufficiently large disk would have a larger mass than its Sun.
A megastructure is a very large artificial object, although the limits of precisely how large vary considerably. Some apply the term to any especially large or tall building. Some sources define a megastructure as an enormous self-supporting artificial construct. The products of megascale engineering or astroengineering are megastructures.
A sphere of influence (SOI) in astrodynamics and astronomy is the oblate-spheroid-shaped region where a particular celestial body exerts the main gravitational influence on an orbiting object. This is usually used to describe the areas in the Solar System where planets dominate the orbits of surrounding objects such as moons, despite the presence of the much more massive but distant Sun.
In physics, specifically classical mechanics, the three-body problem is to take the initial positions and velocities of three point masses that orbit each other in space and calculate their subsequent trajectories using Newton's laws of motion and Newton's law of universal gravitation.
Polydeuces, also designated Saturn XXXIV, is a small trojan moon of Saturn occupying the trailing L5 Lagrange point of Dione. It was discovered by the Cassini Imaging Science Team in images taken by the Cassini space probe on 21 October 2004. With a mean diameter of about 3 km (1.9 mi), Polydeuces is thought to have a smooth surface coated with fine, icy particles accumulated from the cryovolcanic plumes of Enceladus. In its orbit around Saturn, Polydeuces periodically drifts away from Dione's Lagrange point due to gravitational perturbations by other nearby moons of Saturn. Of the four known trojan moons of Saturn, Polydeuces exhibits the largest displacement from its Lagrange point.
In astronomy, perturbation is the complex motion of a massive body subjected to forces other than the gravitational attraction of a single other massive body. The other forces can include a third body, resistance, as from an atmosphere, and the off-center attraction of an oblate or otherwise misshapen body.
In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space at a given moment in time is the gravitational Kepler orbit that it would have around its central body if perturbations were absent. That is, it is the orbit that coincides with the current orbital state vectors.
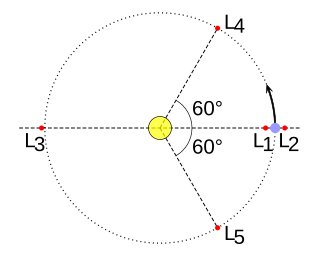
In astronomy, a trojan is a small celestial body (mostly asteroids) that shares the orbit of a larger body, remaining in a stable orbit approximately 60° ahead of or behind the main body near one of its Lagrangian points L4 and L5. Trojans can share the orbits of planets or of large moons.
In physics, the n-body problem is the problem of predicting the individual motions of a group of celestial objects interacting with each other gravitationally. Solving this problem has been motivated by the desire to understand the motions of the Sun, Moon, planets, and visible stars. In the 20th century, understanding the dynamics of globular cluster star systems became an important n-body problem. The n-body problem in general relativity is considerably more difficult to solve due to additional factors like time and space distortions.
In celestial mechanics, a central configuration is a system of point masses with the property that each mass is pulled by the combined gravitational force of the system directly towards the center of mass, with acceleration proportional to its distance from the center. Central configurations are studied in n-body problems formulated in Euclidean spaces of any dimension, although only dimensions one, two, and three are directly relevant for celestial mechanics in physical space.
