The Prandtl number (Pr) or Prandtl group is a dimensionless number, named after the German physicist Ludwig Prandtl, defined as the ratio of momentum diffusivity to thermal diffusivity. The Prandtl number is given as:
In fluid mechanics, the Rayleigh number (Ra, after Lord Rayleigh) for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free (or natural) convection. It characterises the fluid's flow regime: a value in a certain lower range denotes laminar flow; a value in a higher range, turbulent flow. Below a certain critical value, there is no fluid motion and heat transfer is by conduction rather than convection. For most engineering purposes, the Rayleigh number is large, somewhere around 106 to 108.
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to a laminar flow, which occurs when a fluid flows in parallel layers, with no disruption between those layers.

In physics and fluid mechanics, a boundary layer is the thin layer of fluid in the immediate vicinity of a bounding surface formed by the fluid flowing along the surface. The fluid's interaction with the wall induces a no-slip boundary condition. The flow velocity then monotonically increases above the surface until it returns to the bulk flow velocity. The thin layer consisting of fluid whose velocity has not yet returned to the bulk flow velocity is called the velocity boundary layer.

Deflagration is subsonic combustion in which a pre-mixed flame propagates through an explosive or a mixture of fuel and oxidizer. Deflagrations in high and low explosives or fuel–oxidizer mixtures may transition to a detonation depending upon confinement and other factors. Most fires found in daily life are diffusion flames. Deflagrations with flame speeds in the range of 1 m/s differ from detonations which propagate supersonically with detonation velocities in the range of km/s.
In thermodynamics, the heat transfer coefficient or film coefficient, or film effectiveness, is the proportionality constant between the heat flux and the thermodynamic driving force for the flow of heat. It is used in calculating the heat transfer, typically by convection or phase transition between a fluid and a solid. The heat transfer coefficient has SI units in watts per square meter per kelvin (W/m2K).

A premixed flame is a flame formed under certain conditions during the combustion of a premixed charge of fuel and oxidiser. Since the fuel and oxidiser—the key chemical reactants of combustion—are available throughout a homogeneous stoichiometric premixed charge, the combustion process once initiated sustains itself by way of its own heat release. The majority of the chemical transformation in such a combustion process occurs primarily in a thin interfacial region which separates the unburned and the burned gases. The premixed flame interface propagates through the mixture until the entire charge is depleted. The propagation speed of a premixed flame is known as the flame speed which depends on the convection-diffusion-reaction balance within the flame, i.e. on its inner chemical structure. The premixed flame is characterised as laminar or turbulent depending on the velocity distribution in the unburned pre-mixture.
The turbulent Prandtl number (Prt) is a non-dimensional term defined as the ratio between the momentum eddy diffusivity and the heat transfer eddy diffusivity. It is useful for solving the heat transfer problem of turbulent boundary layer flows. The simplest model for Prt is the Reynolds analogy, which yields a turbulent Prandtl number of 1. From experimental data, Prt has an average value of 0.85, but ranges from 0.7 to 0.9 depending on the Prandtl number of the fluid in question.

In fluid dynamics, the Reynolds number is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers, flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow. These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation.
In combustion engineering and explosion studies, the Markstein number characterizes the effect of local heat release of a propagating flame on variations in the surface topology along the flame and the associated local flame front curvature. The dimensionless Markstein number is defined as:
Combustion models for CFD refers to combustion models for computational fluid dynamics. Combustion is defined as a chemical reaction in which a hydrocarbon fuel reacts with an oxidant to form products, accompanied with the release of energy in the form of heat. Being the integral part of various engineering applications like: internal combustion engines, aircraft engines, rocket engines, furnaces, and power station combustors, combustion manifests itself as a wide domain during the design, analysis and performance characteristics stages of the above-mentioned applications. With the added complexity of chemical kinetics and achieving reacting flow mixture environment, proper modeling physics has to be incorporated during computational fluid dynamic (CFD) simulations of combustion. Hence the following discussion presents a general outline of the various adequate models incorporated with the Computational fluid dynamic code to model the process of combustion.
In fluid dynamics, the entrance length is the distance a flow travels after entering a pipe before the flow becomes fully developed. Entrance length refers to the length of the entry region, the area following the pipe entrance where effects originating from the interior wall of the pipe propagate into the flow as an expanding boundary layer. When the boundary layer expands to fill the entire pipe, the developing flow becomes a fully developed flow, where flow characteristics no longer change with increased distance along the pipe. Many different entrance lengths exist to describe a variety of flow conditions. Hydrodynamic entrance length describes the formation of a velocity profile caused by viscous forces propagating from the pipe wall. Thermal entrance length describes the formation of a temperature profile. Awareness of entrance length may be necessary for the effective placement of instrumentation, such as fluid flow meters.
Chemical reaction models transform physical knowledge into a mathematical formulation that can be utilized in computational simulation of practical problems in chemical engineering. Computer simulation provides the flexibility to study chemical processes under a wide range of conditions. Modeling of a chemical reaction involves solving conservation equations describing convection, diffusion, and reaction source for each component species.
The Darrieus–Landau instability or hydrodynamic instability is an instrinsic flame instability that occurs in premixed flames, caused by the density variation due to the thermal expansion of the gas produced by the combustion process. In simple terms, the stability inquires whether a steadily propagating plane sheet with a discontinuous jump in density is stable or not. It was predicted independently by Georges Jean Marie Darrieus and Lev Landau. Yakov Zeldovich notes that Lev Landau generously suggested this problem to him to investigate and Zeldovich however made error in calculations which led Landau himself to complete the work.
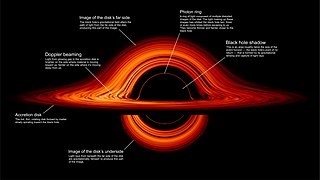
An accretion disk is a structure formed by diffuse material in orbital motion around a massive central body. The central body is most frequently a star. Friction, uneven irradiance, magnetohydrodynamic effects, and other forces induce instabilities causing orbiting material in the disk to spiral inward toward the central body. Gravitational and frictional forces compress and raise the temperature of the material, causing the emission of electromagnetic radiation. The frequency range of that radiation depends on the central object's mass. Accretion disks of young stars and protostars radiate in the infrared; those around neutron stars and black holes in the X-ray part of the spectrum. The study of oscillation modes in accretion disks is referred to as diskoseismology.
In combustion, the Karlovitz number is defined as the ratio of chemical time scale to Kolmogorov time scale , named after Béla Karlovitz. The number reads as
The Zel'dovich number is a dimensionless number which provides a quantitative measure for the activation energy of a chemical reaction which appears in the Arrhenius exponent, named after the Russian scientist Yakov Borisovich Zel'dovich, who along with David A. Frank-Kamenetskii, first introduced in their paper in 1938. In 1983 ICDERS meeting at Poitiers, it was decided to name after Zel'dovich.
Activation energy asymptotics (AEA), also known as large activation energy asymptotics, is an asymptotic analysis used in the combustion field utilizing the fact that the reaction rate is extremely sensitive to temperature changes due to the large activation energy of the chemical reaction.
In combustion, flame stretch is a quantity which measures the amount of stretch of the flame surface due to curvature and due to the outer velocity field strain. The early concept of flame stretch was introduced by Karlovitz in 1953, although the correct definition was introduced two decades later by Forman A. Williams in 1975. George H. Markstein studied flame stretch by treating the flame surface as a hydrodynamic discontinuity. The flame stretch is also discussed by Bernard Lewis and Guenther von Elbe in their book. All these discussions treated flame stretch as an effect of flow velocity gradients. The stretch can be found even if there is no velocity gradient, but due to the flame curvature. So, the definition required a more general formulation and its precise definition was first introduced by Forman A. Williams in 1975 as the ratio of rate of change of flame surface area to the area itself
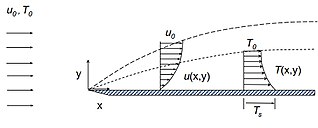
This page describes some parameters used to characterize the properties of the thermal boundary layer formed by a heated fluid moving along a heated wall. In many ways, the thermal boundary layer description parallels the velocity (momentum) boundary layer description first conceptualized by Ludwig Prandtl. Consider a fluid of uniform temperature and velocity impinging onto a stationary plate uniformly heated to a temperature . Assume the flow and the plate are semi-infinite in the positive/negative direction perpendicular to the plane. As the fluid flows along the wall, the fluid at the wall surface satisfies a no-slip boundary condition and has zero velocity, but as you move away from the wall, the velocity of the flow asymptotically approaches the free stream velocity . The temperature at the solid wall is and gradually changes to as one moves toward the free stream of the fluid. It is impossible to define a sharp point at which the thermal boundary layer fluid or the velocity boundary layer fluid becomes the free stream, yet these layers have a well-defined characteristic thickness given by and . The parameters below provide a useful definition of this characteristic, measurable thickness for the thermal boundary layer. Also included in this boundary layer description are some parameters useful in describing the shape of the thermal boundary layer.








