Area is the measure of a region's size on a surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid . Two different regions may have the same area ; by synecdoche, "area" sometimes is used to refer to the region, as in a "polygonal area".
In geometry, a cube or regular hexahedron is a three-dimensional solid object bounded by six congruent square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron.
In geometry, an octahedron is a polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. Many types of irregular octahedra also exist, including both convex and non-convex shapes.
A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.
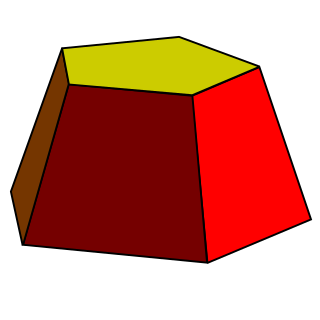
In geometry, a frustum ; is the portion of a solid that lies between two parallel planes cutting the solid. In the case of a pyramid, the base faces are polygonal and the side faces are trapezoidal. A right frustum is a right pyramid or a right cone truncated perpendicularly to its axis; otherwise, it is an oblique frustum. In a truncated cone or truncated pyramid, the truncation plane is not necessarily parallel to the cone's base, as in a frustum. If all its edges are forced to become of the same length, then a frustum becomes a prism.
In geometry, a solid angle is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle at that point.
The Method of Mechanical Theorems, also referred to as The Method, is one of the major surviving works of the ancient Greek polymath Archimedes. The Method takes the form of a letter from Archimedes to Eratosthenes, the chief librarian at the Library of Alexandria, and contains the first attested explicit use of indivisibles. The work was originally thought to be lost, but in 1906 was rediscovered in the celebrated Archimedes Palimpsest. The palimpsest includes Archimedes' account of the "mechanical method", so called because it relies on the center of weights of figures (centroid) and the law of the lever, which were demonstrated by Archimedes in On the Equilibrium of Planes.
In geometry, a prism is a polyhedron comprising an n-sided polygon base, a second base which is a translated copy of the first, and n other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.
Solid geometry or stereometry is the geometry of three-dimensional Euclidean space . A solid figure is the region of 3D space bounded by a two-dimensional closed surface; for example, a solid ball consists of a sphere and its interior.
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.
A cylinder has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
In geometry, a square pyramid is a pyramid with a square base, having a total of five faces. If the apex of the pyramid is directly above the center of the square, it is a right square pyramid with four isosceles triangles; otherwise, it is an oblique square pyramid. When all of the pyramid's edges are equal in length, its triangles are all equilateral. It is called an equilateral square pyramid, an example of a Johnson solid.
In geometry and science, a cross section is the non-empty intersection of a solid body in three-dimensional space with a plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections. The boundary of a cross-section in three-dimensional space that is parallel to two of the axes, that is, parallel to the plane determined by these axes, is sometimes referred to as a contour line; for example, if a plane cuts through mountains of a raised-relief map parallel to the ground, the result is a contour line in two-dimensional space showing points on the surface of the mountains of equal elevation.
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the nth polygon and the containing shape will become arbitrarily small as n becomes large. As this difference becomes arbitrarily small, the possible values for the area of the shape are systematically "exhausted" by the lower bound areas successively established by the sequence members.
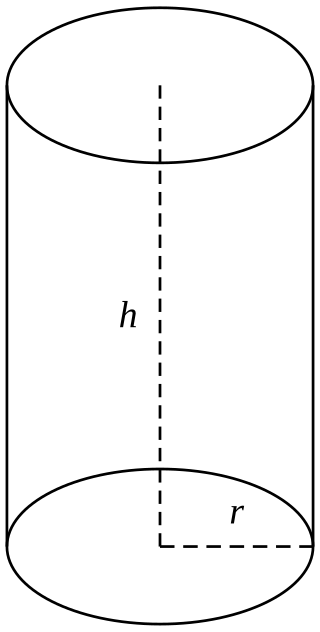
A right circular cylinder is a cylinder whose generatrices are perpendicular to the bases. Thus, in a right circular cylinder, the generatrix and the height have the same measurements. It is also less often called a cylinder of revolution, because it can be obtained by rotating a rectangle of sides and around one of its sides. Fixing as the side on which the revolution takes place, we obtain that the side , perpendicular to , will be the measure of the radius of the cylinder.
In geometry, a hypercone is the figure in the 4-dimensional Euclidean space represented by the equation
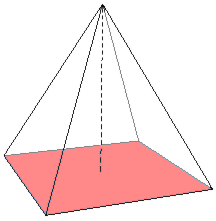
In geometry, a base is a side of a polygon or a face of a polyhedron, particularly one oriented perpendicular to the direction in which height is measured, or on what is considered to be the "bottom" of the figure. This term is commonly applied in plane geometry to triangles, parallelograms, trapezoids, and in solid geometry to cylinders, cones, pyramids, parallelepipeds, prisms, and frustums.
In geometry, Cavalieri's principle, a modern implementation of the method of indivisibles, named after Bonaventura Cavalieri, is as follows:
In four-dimensional geometry, the spherinder, or spherical cylinder or spherical prism, is a geometric object, defined as the Cartesian product of a 3-ball of radius r1 and a line segment of length 2r2:
