In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and explores the relationships between these classifications. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm.

A finite-state machine (FSM) or finite-state automaton, finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed.

In computational complexity theory, NP is a complexity class used to classify decision problems. NP is the set of decision problems for which the problem instances, where the answer is "yes", have proofs verifiable in polynomial time by a deterministic Turing machine, or alternatively the set of problems that can be solved in polynomial time by a nondeterministic Turing machine.
In theoretical computer science, a nondeterministic Turing machine (NTM) is a theoretical model of computation whose governing rules specify more than one possible action when in some given situations. That is, an NTM's next state is not completely determined by its action and the current symbol it sees, unlike a deterministic Turing machine.

In the theory of computation, a branch of theoretical computer science, a pushdown automaton (PDA) is a type of automaton that employs a stack.

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a finite automaton (FA) or finite-state machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.
In theoretical computer science, a probabilistic Turing machine is a non-deterministic Turing machine that chooses between the available transitions at each point according to some probability distribution. As a consequence, a probabilistic Turing machine can—unlike a deterministic Turing Machine—have stochastic results; that is, on a given input and instruction state machine, it may have different run times, or it may not halt at all; furthermore, it may accept an input in one execution and reject the same input in another execution.

In computational complexity theory, a complexity class is a set of computational problems "of related resource-based complexity". The two most commonly analyzed resources are time and memory.
In computer science, parameterized complexity is a branch of computational complexity theory that focuses on classifying computational problems according to their inherent difficulty with respect to multiple parameters of the input or output. The complexity of a problem is then measured as a function of those parameters. This allows the classification of NP-hard problems on a finer scale than in the classical setting, where the complexity of a problem is only measured as a function of the number of bits in the input. This appears to have been first demonstrated in Gurevich, Stockmeyer & Vishkin (1984). The first systematic work on parameterized complexity was done by Downey & Fellows (1999).

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.
In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if
In computational complexity theory, P, also known as PTIME or DTIME(nO(1)), is a fundamental complexity class. It contains all decision problems that can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.
In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time .
In computational complexity theory, an alternating Turing machine (ATM) is a non-deterministic Turing machine (NTM) with a rule for accepting computations that generalizes the rules used in the definition of the complexity classes NP and co-NP. The concept of an ATM was set forth by Chandra and Stockmeyer and independently by Kozen in 1976, with a joint journal publication in 1981.
In computability theory and computational complexity theory, a reduction is an algorithm for transforming one problem into another problem. A sufficiently efficient reduction from one problem to another may be used to show that the second problem is at least as difficult as the first.
In computational complexity theory, NL is the complexity class containing decision problems that can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space.
In automata theory, a deterministic pushdown automaton is a variation of the pushdown automaton. The class of deterministic pushdown automata accepts the deterministic context-free languages, a proper subset of context-free languages.

In computational complexity theory and circuit complexity, a Boolean circuit is a mathematical model for combinational digital logic circuits. A formal language can be decided by a family of Boolean circuits, one circuit for each possible input length.
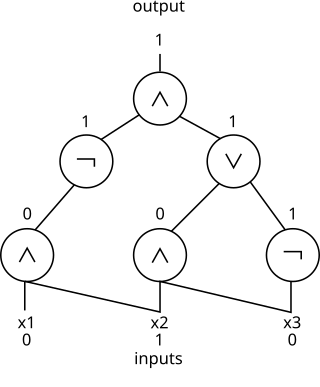
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of the Boolean circuits that compute them. A related notion is the circuit complexity of a recursive language that is decided by a uniform family of circuits .
In computational complexity theory, a certificate is a string that certifies the answer to a computation, or certifies the membership of some string in a language. A certificate is often thought of as a solution path within a verification process, which is used to check whether a problem gives the answer "Yes" or "No".






